计算机图形处理完整解析：从像素到3D渲染的演进之旅


# 摘要
计算机图形处理是一个涵盖广泛技术的领域，它从二维图形处理的基础出发，扩展到三维建模、渲染技术以及图形处理软件的运用。本文首先介绍了计算机图形处理的起源与基础，随后详细探讨了二维图形处理技术中的像素概念、图像表示、绘制算法和GUI设计原则。在三维图形处理方面，文章深入分析了三维空间的数学基础、建模技术、纹理和材质处理，以及三维渲染技术中的光线追踪、着色器编程和后期处理技术。最后，本文探讨了图形处理软件和工具的使用，并对未来趋势，包括VR/AR、云计算和人工智能在图形处理中的应用前景进行了展望，指出这些技术的发展为图形处理带来了新的挑战和机遇。

# 关键字
计算机图形处理；二维图形技术；三维建模；渲染技术；图形处理软件；VR/AR技术

参考资源链接：[(完整word版)计算机组成与系统结构课后答案全(清华大学出版社-袁春风主编).doc](https://wenku.csdn.net/doc/2drb05tvkk?spm=1055.2635.3001.10343)
# 1. 计算机图形处理的起源与基础

## 1.1 图形处理的诞生与早期发展
计算机图形处理的历史可追溯至20世纪50年代，那时，科学家们开始研究如何使用数字计算机来生成和操控图形。早期的图形处理主要依赖于向量图形，即通过数学公式来描述图形的形状，这种方法在当时主要用于制图和工程设计。

随着技术的进步，像素开始取代向量图形成为主流，图形处理开始进入以像素为基础的图像表示时代。像素，即图像的最小元素单位，可以通过不同的颜色模型来表达丰富的色彩信息。这一时期，人们开始对图形显示设备、图像存储格式以及图像压缩技术进行了深入研究。

## 1.2 基本概念的演变与技术突破
计算机图形学的基础概念，如“图形”、“图像”以及“渲染”等，随着时间的推移不断演变。图形主要是指以数学模型定义的抽象几何形状，而图像则是光的视觉表现。渲染则是将三维模型转换为二维图像的过程，这对于影视特效、游戏开发以及模拟仿真等领域至关重要。

在这一时期，图形处理领域也经历了一系列的技术突破，包括图形硬件的改进、显示技术的发展以及渲染算法的创新。这些技术突破为图形学的进一步发展奠定了坚实的基础，并催生了一系列新的应用场景和研究方向。

## 1.3 当代计算机图形处理的意义
当代计算机图形处理已经渗透到我们生活的方方面面，从网页设计、视频游戏、电影特效到虚拟现实和增强现实，无一不依赖于先进的图形处理技术。这些技术不仅提升了用户体验，还为科研、教育和娱乐行业提供了强大的支持工具。

随着计算机硬件性能的不断提升和算法的持续优化，计算机图形处理正在不断发展，呈现出更加逼真的视觉效果和更高效的工作流程。因此，对于从业者来说，理解其起源与基础对于把握未来的趋势和应对挑战都具有十分重要的意义。

# 2. 二维图形处理技术

## 2.1 像素基础与图像表示

### 2.1.1 像素概念和颜色模型

在二维图形处理的世界里，像素（Pixel）是构成数字图像的最小单位，它代表了图像中的一个点，包含了颜色信息。要深入理解二维图形处理技术，首先需要掌握像素的基本概念和颜色模型。

像素是"Picture Element"的缩写，它是图像数字化的基础。每个像素都具有特定的颜色值，这些值定义了在图像中的显示效果。计算机图形学中常见的颜色模型有RGB颜色模型、CMYK颜色模型和HSB颜色模型。

RGB颜色模型广泛应用于计算机屏幕和互联网上。它基于红、绿、蓝三种颜色光的不同强度组合来表现其他颜色，每种颜色通过一个0到255的数值范围来表示。

flowchart LR
A[开始] --> B[创建像素对象]
B --> C[定义RGB值]
C --> D[显示像素]
D --> E[调整RGB值改变颜色]
E --> F[结束]

RGB值通过三原色的组合产生各种颜色，例如(255, 0, 0)代表纯红色。当三个分量的值都是255时，表示的是白色；当都是0时，表示的是黑色。

### 2.1.2 图像文件格式和压缩技术

图像文件格式是用于存储数字图像数据的编码方式。常见的图像文件格式包括JPEG, PNG, GIF, BMP等。每种格式都有其特点和使用场景，比如JPEG适用于照片，而PNG适用于带有透明背景的图像。

图像压缩技术可以帮助减少图像文件的大小，便于存储和传输，同时尽可能保持图像质量。无损压缩与有损压缩是两种主要的压缩技术。无损压缩如PNG，通过算法删除文件中的冗余数据而不丢失信息。有损压缩如JPEG，则在压缩过程中丢弃一些图像数据，牺牲一定的图像质量以达到更高的压缩率。

## 2.2 二维图形绘制算法

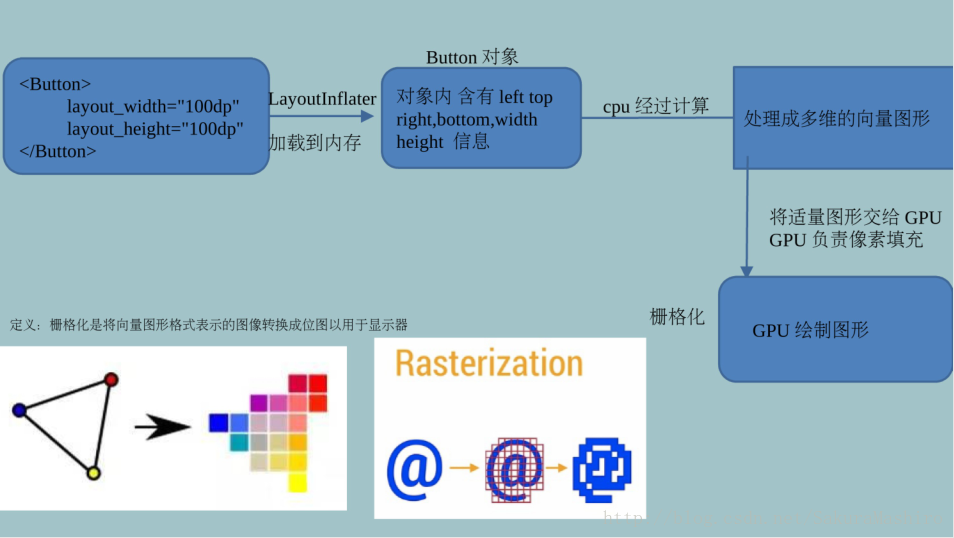
### 2.2.1 矢量图形与栅格图形的对比

在二维图形处理中，矢量图形与栅格图形是两种基本的图形表示方法。矢量图形使用几何原语（如线条、矩形、曲线和多边形）定义图形，具有无限缩放而不失真的特性。而栅格图形（也称为位图图像）由像素矩阵组成，它们在放大到一定程度后会出现锯齿和模糊。

**矢量图形**的核心在于用数学公式来描述形状，使得图形文件相对较小，并且可以在不同分辨率下保持清晰。矢量图形应用广泛，包括标志、字体、机械绘图和矢量插图。

**栅格图形**则以像素网格的形式存储图像信息，适合表现颜色丰富的图片，比如摄影照片。然而，栅格图形在放大或缩小的时候，无法像矢量图形一样保持平滑的边缘。

### 2.2.2 常用的图形绘制技术

在二维图形处理中，有许多常用的图形绘制技术，这些技术包括但不限于线条绘制、矩形绘制、圆角矩形绘制以及贝塞尔曲线等。这些基础图形绘制技术为复杂图形的生成提供了必要的构建块。

**线条绘制**是图形处理中最基本的操作之一，通常通过指定起点和终点坐标来完成。**矩形绘制**相对简单，需要提供左上角和右下角的坐标。而**圆角矩形绘制**需要额外指定圆角的半径。**贝塞尔曲线**则是一种可以绘制平滑曲线的技术，通过控制点来确定曲线的形状。

import matplotlib.pyplot as plt
import numpy as np

# 定义贝塞尔曲线控制点
ctrlpoints = np.array([[0, 1], [2, 2], [3, 0], [5, 1]])

# 计算贝塞尔曲线
t = np.linspace(0, 1, 100)
curve = (1-t)**3 * ctrlpoints[0] + \
        3*(1-t)**2 * t * ctrlpoints[1] + \
        3*(1-t) * t**2 * ctrlpoints[2] + \
        t**3 * ctrlpoints[3]

# 绘制结果
plt.plot(curve[:,0], curve[:,1])
plt.plot(ctrlpoints[:,0], ctrlpoints[:,1], 'ro-')
plt.show()

在上述Python代码中，使用了matplotlib库来绘制一个贝塞尔曲线。代码中，首先定义了控制点数组，然后通过计算得到了曲线上的点，并最终绘制出贝塞尔曲线和控制点。

## 2.3 图形用户界面(GUI)设计

### 2.3.1 GUI元素与布局设计原则

图形用户界面（GUI）的设计是构建直观、易用的用户交互界面的关键。GUI由各种控件（如按钮、文本框、滑块等）组成，它们通过布局管理器来组织在界面上的位置和大小。

GUI设计的基本原则包括一致性、简洁性和直观性。一致性要求界面元素的风格和行为保持一致，以减少用户的认知负担。简洁性是指界面应避免过度复杂，保持清晰的视觉层次。直观性则意味着界面元素应该易于理解，让用户能够快速掌握其用途。

### 2.3.2 交云用户界面的交互技术

交互技术是GUI设计中不可或缺的一部分，它包括如何响应用户的输入以及如何通过视觉反馈进行有效沟通。常见的交互技术包括点击、拖放、悬停提示等。

在现代的GUI设计中，设计师越来越多地利用交云技术来增强用户体验。交云技术（如动画和过渡效果）可以提高界面的动态感和自然性，使用户在使用应用时感到更加流畅和舒适。

设计师还需要考虑无障碍性设计，确保应用对所有用户都是可访问的，包括有视觉、听觉或运动障碍的用户。通过使用合适的颜色对比度、清晰的字体和辅助技术，可以显著提高应用的无障碍性。

在下一章节中，我们将进一步探讨三维图形处理的基础知识，包括三维空间的数学基础和三维建模技术，深入理解它们对于提升图形处理能力至关重要。

# 3. 三维图形基础与建模

三维图形的创建和处理已经成为计算机图形处理领域中的核心技术。从简单的三维模型构建到复杂的场景渲染，都需要对三维空间、几何体、建模技术、纹理和材质处理有深入的理解。本章节将逐步展开对三维图形基础与建模技术的探讨，从数学基础到具体的应用技术，为读者提供全面的学习路径。

## 3.1 三维空间的数学基础

三维空间的数学基础是建立在点、向量和矩阵的理论之上的。这些数学概念在三维图形的表示和变换中扮演了至关重要的角色。理解这些概念对于任何想要深入研究三维图形的人来说都是必不可少的。

### 3.1.1 点、向量和矩阵在三维空间的应用

在三维空间中，点表示空间中的一个位置，而向量则表示具有大小和方向的量。点和向量是三维图形处理的基础元素，用于定义图形的形状和位置。向量运算，如点积和叉积，在计算距离、角度、以及面的法线方向中有着广泛的应用。

矩阵在三维图形中的应用主要体现在坐标变换上，如平移、旋转和缩放。矩阵运算能够高效地描述和执行这些变换，是三维图形管线中不可或缺的一环。

#### 代码块示例

% MATLAB代码示例：使用矩阵进行三维坐标变换

% 定义一个点
point = [1; 2; 3];

% 定义一个3x3旋转矩阵
rotationMatrix = [cos(theta) -sin(theta) 0;
                  sin(theta)  cos(theta) 0;
                  0           0        1];

% 应用旋转矩阵变换点
rotatedPoint = rotationMatrix * point;

% 显示变换后的点
disp(rotatedPoint);

#### 参数说明和逻辑分析
上述代码使用了MATLAB语言来演示一个点在三维空间中通过旋转矩阵进行变换的过程。`point`变量定义了要变换的三维点，`rotationMatrix`变量定义了一个围绕Z轴旋转的矩阵。代码执行后的结果是展示经过旋转后的点坐标。

### 3.1.2 投影变换与视图变换

投影变换是指将三维物体