算法复杂度：时间与空间权衡的艺术


# 摘要
本文深入探讨了算法复杂度的两个核心概念：时间复杂度与空间复杂度。文章首先介绍了时间复杂度的理论基础，包括其定义、表示方法以及分析方法，并详细阐述了影响时间复杂度的关键因素。接着，文章转向空间复杂度的讨论，解释了空间复杂度的评估标准和优化策略，并探讨了时间与空间复杂度之间的权衡关系。通过分析常见算法和数据结构的实际案例，本文揭示了时间复杂度和空间复杂度优化的实战应用，并最终强调了在系统设计中对复杂度分析的重要性。

# 关键字
算法复杂度；时间复杂度；空间复杂度；优化策略；权衡关系；系统设计

参考资源链接：[算法设计与分析（第2版）课后习题答案解析](https://wenku.csdn.net/doc/4ff9g7jc3z?spm=1055.2635.3001.10343)
# 1. 算法复杂度的基本概念

在计算机科学中，算法复杂度是用来评估算法运行效率的度量标准，它能帮助我们理解算法的性能和资源需求。算法复杂度主要分为两大类：时间复杂度和空间复杂度。时间复杂度衡量的是算法执行时间与输入数据量之间的关系，而空间复杂度衡量的是算法在执行过程中对内存空间的需求量。

理解复杂度的基本概念对于设计高效的算法至关重要。不同算法的复杂度会直接影响到程序运行的速度和资源消耗。例如，一个时间复杂度较低但空间复杂度较高的算法，可能会在速度上表现优秀，但会占用大量内存资源。反之亦然。因此，算法设计者需要根据实际情况，在时间和空间资源之间进行权衡。

在后续章节中，我们将深入探讨时间复杂度和空间复杂度的详细理论基础和实战应用，揭示如何通过复杂度分析来优化算法，提升程序的整体性能。

# 2. 时间复杂度的理论基础

### 2.1 时间复杂度的定义和表示方法

时间复杂度是衡量算法运行时间与输入数据大小之间的关系的度量，是算法效率的抽象表示。在实际应用中，我们通常关注算法的最坏情况执行时间，以确保算法在任何情况下都有良好的性能表现。

#### 2.1.1 大O表示法
大O表示法是一种描述函数渐进行为的方法。例如，如果一个算法的运行时间与输入数据的大小n成正比，我们说这个算法的时间复杂度是O(n)。大O后面的表达式只包含最高次项，并忽略常数系数和低次项，因为随着n的增大，它们对总体运行时间的影响可以忽略不计。

举例来说，以下是一个简单的线性搜索算法，它遍历数组中的每个元素，返回第一个匹配项的索引：

def linear_search(arr, target):
    for index, value in enumerate(arr):
        if value == target:
            return index
    return -1

这段代码的时间复杂度分析为O(n)，因为算法的执行时间与数组`arr`的大小成线性关系。

#### 2.1.2 常见时间复杂度的分类与示例
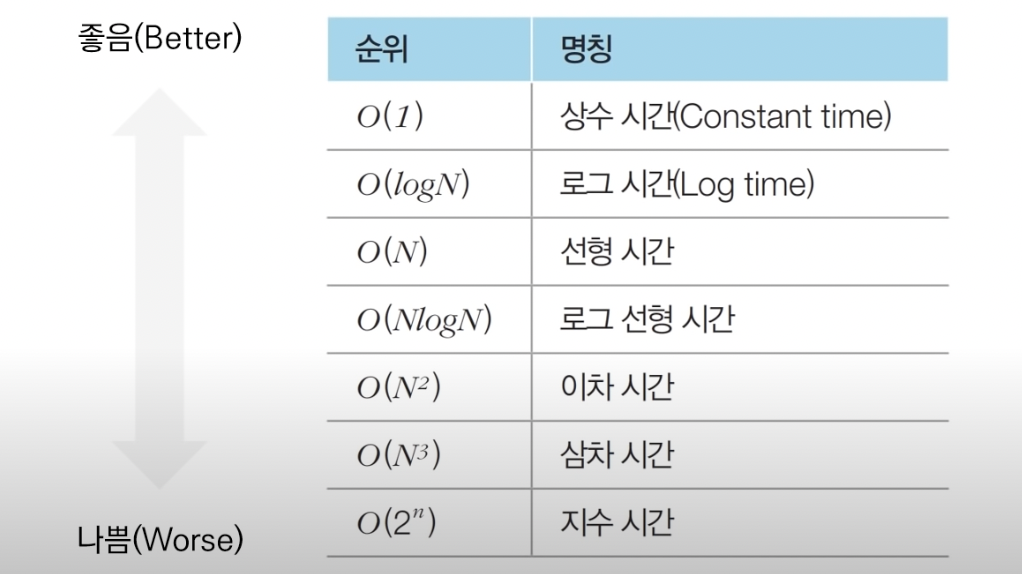
时间复杂度的分类涵盖了从常数时间到指数时间的各种情况。以下是一些常见的复杂度类型，以及每种复杂度对应的典型算法：

- 常数时间：O(1)。例如，访问数组中的特定元素。
- 对数时间：O(log n)。例如，二分查找算法。
- 线性时间：O(n)。例如，线性搜索算法。
- 线性对数时间：O(n log n)。例如，快速排序算法。
- 二次时间：O(n^2)。例如，简单的冒泡排序算法。
- 指数时间：O(2^n)。例如，递归计算斐波那契数列。

### 2.2 时间复杂度的分析方法

#### 2.2.1 渐进分析
渐进分析是指在算法的输入数据趋向无穷大时，算法性能的变化趋势。它关注的是算法运行时间随着输入规模n增加而如何增长。我们通常不会精确计算算法的运行时间，而是使用大O表示法来描述这种趋势。

#### 2.2.2 递推式与递归树方法
递推式是一种递归关系的数学表达，可以用来分析递归算法的时间复杂度。递归树方法是一种图形化的分析技术，它将递归算法的每一步抽象成树形结构，通过观察树的层级和分支数量，可以计算出算法的时间复杂度。

以归并排序为例，其递推式为T(n) = 2T(n/2) + Θ(n)，使用递归树方法分析可得其时间复杂度为O(n log n)。

### 2.3 时间复杂度的影响因素

#### 2.3.1 算法中的循环与递归
循环和递归是算法中影响时间复杂度的主要结构。循环决定了算法必须执行的基本操作次数，而递归则涉及了子问题的分解与解决，它们直接关联到算法的性能表现。

例如，双重循环的嵌套将导致算法的时间复杂度从O(n)变成O(n^2)。

#### 2.3.2 数据结构的选择与优化
不同的数据结构具有不同的时间复杂度特性。选择合适的数据结构是优化算法性能的关键，例如使用哈希表可以将查找时间从O(n)降低到O(1)。

以上就是对时间复杂度理论基础的介绍。下一章节我们将深入探讨空间复杂度，了解它是如何与时间复杂度相互影响，以及如何在实际应用中进行优化。

# 3. 空间复杂度的理论基础

在前一章节中，我们了解了时间复杂度的相关知识，本章节我们将深入探讨空间复杂度。空间复杂度是算法设计中极为重要的一个考量维度，它关注算法在运行过程中临时占用存储空间的大小。本章将介绍空间复杂度的基本概念、评估标准，以及优化策略，并详细探讨空间与时间之间的权衡问题。

## 3.1 空间复杂度的定义和评估标准

### 3.1.1 空间复杂度的表示法

空间复杂度描述了算法执行过程中，对数据存储空间的占用量。它通常用大O符号来表示，如O(1)、O(n)等。在分析空间复杂度时，我们主要关注两部分：常量空间和可变空间。

- **常量空间**：这部分空间与输入数据的大小无关，通常是固定大小的，比如一些基本数据类型的变量、程序计数器等。
- **可变空间**：这部分空间与输入数据的规模成正比，是空间复杂度分析的主要关注点，比如数组、栈、树等数据结构。

### 3.1.2 内存使用分析

分析内存使用情况时，我们需要考虑以下几点：

- **局部变量**：函数内部声明的变量通常分配在栈上，其空间大小是固定的。
- **动态分配**：使用如 `malloc` 或 `new` 动态申请的内存，其大小随算法运行而变化。
- **递归调用栈**：每次递归调用都会在调用栈上分配新的空间，递归深度越大，空间复杂度越高。

#### 代码块示例

int sum(int n) {
    if (n == 0) return 0;
    return n + sum(n - 1);
}

上述递归函数计算从1到n的整数和。尽管递归深度为n，但实际上，由于每次递归调用只存储了n和返回地址，这个函数的空间复杂度为O(1)，并非O(n)。

## 3.2 空间复杂度优化策略

### 3.2.1 数据存储优化

在算法中，数据存储方式会直接影响空间复杂度。例如：

- **使用数组代替链表**：对于需要频繁随机访问的场景，数组的空间效率通常优于链表。
- **压缩数据**：对于存储大量重复数据的情况，可以使用哈夫曼树或游程编码等方法压缩数据，节省空间。

### 3.2.2 算法优化减少空间需求

算法设计阶段，通过优化算法的内部结构，可以减少空间使用，例如：

- **原地算法**：尽量在原数据上进行操作，避免使用额外的空间。例如，在数组中进行排序操作，就应优先选