Origin矩阵运算与分析：掌握这些方法与案例让你与众不同


参考资源链接：[Origin入门：数据求导详解及环境定制教程](https://wenku.csdn.net/doc/45o4pqn57q?spm=1055.2635.3001.10343)
# 1. 矩阵运算的基础知识

在数学、物理、工程学以及信息技术等诸多领域，矩阵运算一直扮演着不可或缺的角色。它不仅是线性代数的核心组成部分，更是现代计算技术的基础。矩阵，作为一种特殊的二维数组，能够以高度凝练的方式表示和处理数据与信息。而矩阵运算，包括加法、减法、乘法和转置等基础操作，则为更高级的数据分析技术提供了支持。

## 1.1 矩阵的定义及类型

矩阵是由数字或数学表达式组成的矩形阵列，可以看作是一系列行向量或列向量的集合。其核心特性包括行数、列数以及存储的数值类型，由此衍生出不同类型的矩阵，例如零矩阵、单位矩阵、对角矩阵、稀疏矩阵等，每一类都有其特定的性质和应用场景。

## 1.2 矩阵运算的规则

矩阵运算遵循特定的规则，比如同型矩阵才能进行加减运算，而乘法运算则需要满足行数与另一矩阵的列数相匹配。矩阵的乘法不满足交换律，但满足结合律和分配律，这些规则为处理复杂问题提供了便捷的工具。转置操作是矩阵运算中的重要概念，它将矩阵的行和列互换，为特定类型的矩阵运算和证明提供了方便。

# 2. Origin矩阵运算的理论基础

## 2.1 矩阵运算的基本概念

### 2.1.1 矩阵定义及类型

矩阵是由数字排列成的矩形阵列，是线性代数的核心概念之一。矩阵中的数字称为矩阵的元素。根据元素的排列和矩阵的维度，矩阵可以分为不同种类，例如：

- 行向量和列向量：它们分别是一维矩阵，行向量是只有一行的矩阵，而列向量是只有一列的矩阵。
- 方阵：行数和列数相等的矩阵。方阵常用于表示线性变换，且拥有独特的数学性质，比如行列式。
- 对角矩阵：方阵中除主对角线以外的元素都是零。对角矩阵在线性代数中用于简化运算。
- 零矩阵：所有元素都为零的矩阵，其维度可以是任意的。

矩阵运算通常涉及矩阵间的加法、减法、乘法等操作，以及转置等变换。矩阵的这些操作在数学和工程领域有广泛的应用。

### 2.1.2 矩阵运算的规则

矩阵运算遵循特定的数学规则，其中加法和乘法是最基本的运算。

- 加法：两个矩阵相加，要求矩阵具有相同的维度。元素对应相加，操作非常直观。
- 数乘：一个矩阵与一个标量相乘，实际上是将矩阵的每个元素与该标量相乘。
- 乘法：两个矩阵相乘，第一个矩阵的列数必须与第二个矩阵的行数相等。结果矩阵的维度为第一个矩阵的行数乘以第二个矩阵的列数。

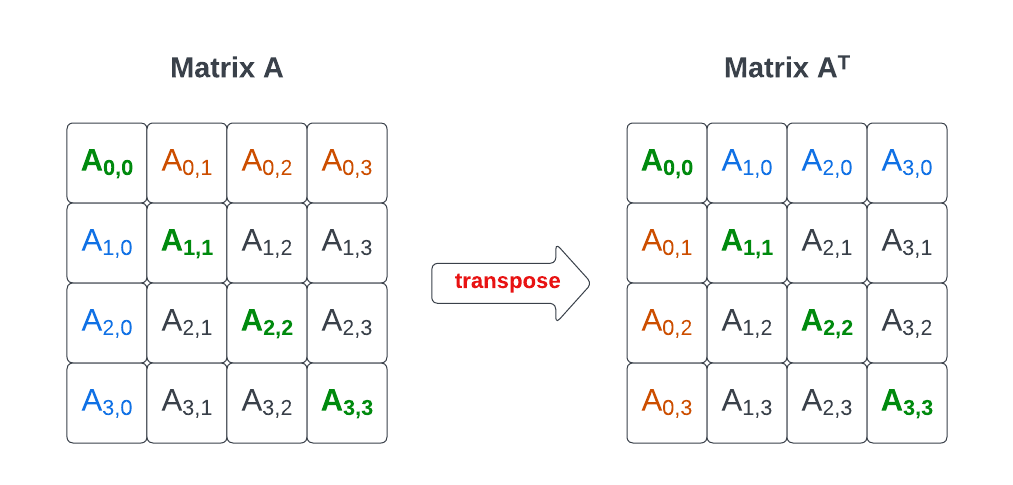
矩阵的转置是将矩阵的行和列互换位置，矩阵A的转置记作A^T。转置操作在求解线性方程组、分析对称性时非常有用。

## 2.2 矩阵运算的数学原理

### 2.2.1 线性代数的基础知识

线性代数提供了矩阵运算的数学基础，其核心概念包括向量空间、基、维度等。在Origin中进行矩阵运算，需要掌握线性代数的基础知识：

- 向量空间：一组向量形成的集合，具有向量加法和数乘运算，并满足八条公理。
- 线性独立和线性相关：向量组中的某些向量如果不能通过线性组合得到其他向量，则称它们线性独立，否则线性相关。
- 基和维度：一组最大线性无关向量组构成空间的基，基中向量的数量称为维度。
- 子空间：由向量空间的子集构成的，满足向量空间定义的集合。

理解这些概念，有助于我们更好地在Origin中利用矩阵进行数据分析和处理。

### 2.2.2 矩阵运算在数学中的应用

矩阵运算是解决线性方程组的主要工具之一，此外它还在多领域有广泛的应用：

- 线性方程组：可以使用矩阵表示线性方程组，进而通过矩阵运算求解。
- 线性变换：矩阵可以表示向量空间的线性变换，如旋转、缩放等。
- 特征值和特征向量：在很多领域，例如物理动力学和量子力学中，特征值和特征向量是核心概念，它们通过矩阵运算得到。
- 统计学：多变量统计分析常用到协方差矩阵和相关性分析。

掌握这些应用，对于使用Origin进行矩阵运算至关重要，能够帮助我们更加高效地处理数据和分析问题。

## 2.3 Origin中的矩阵操作界面

### 2.3.1 Origin的用户界面介绍

Origin的用户界面分为几个主要部分：菜单栏、工具栏、图形窗口和工作表。其中，在矩阵运算方面：

- 菜单栏提供了矩阵操作的入口，例如矩阵分析、矩阵计算等。
- 工具栏提供了快捷操作按钮，能够快速执行常见的矩阵运算。
- 图形窗口用于展示矩阵运算的结果，如矩阵图和矩阵间的比较图。
- 工作表用于输入和显示矩阵数据，可以直接在这里编辑矩阵。

理解Origin的界面布局，有助于更高效地进行矩阵操作和数据分析。

### 2.3.2 Origin矩阵运算的菜单与工具

在Origin中，矩阵运算可以通过以下方式执行：

- 矩阵计算菜单：提供了矩阵加减乘除、转置、逆矩阵计算等操作。
- 专业分析工具：包含特征值和特征向量求解、矩阵分解等高级分析功能。
- 脚本窗口：Origin支持矩阵运算的脚本编写，脚本窗口允许用户通过编程方式实现复杂的矩阵计算。

借助这些功能，Origin用户可以完成从基本到高级的各种矩阵运算任务。

在第三章，我们将详细介绍Origin中的矩阵分析工具，并通过实例展示这些工具的应用。

# 3. Origin矩阵分析工具详解

Origin软件提供了一系列矩阵分析工具，这些工具不仅包括基本的矩阵运算功能，还包括了更为复杂的矩阵分析技术。在本章节中，我们将深入了解这些工具的使用方法，并通过实例展示它们在实际应用中的强大能力。

## 3.1 基本矩阵分析功能

### 3.1.1 矩阵加减乘除和转置

Origin的矩阵分析功能允许用户执行基本的矩阵运算。矩阵加减乘除是矩阵运算中的基本操作，它们在处理数据和解决线性方程组时有着广泛的应用。而矩阵转置是将矩阵的行换成列，列换成行的操作，这对矩阵分析尤为重要。

在Origin中，这些操作可以通过矩阵对象或矩阵数据表来执行。例如，以下代码展示了如何在Origin中创建两个矩阵并进行加法运算：

// 创建两个3x3矩阵A和B
A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
B = [9, 8, 7; 6, 5, 4; 3, 2, 1];

// 加法运算
C = A + B;
// 转置运算
D = C';

### 3.1.2 矩阵的行列式和逆矩阵计算

计算矩