1. 多变量分析基础与Origin软件概述

多变量分析是一种复杂的数据分析技术，涉及多个变量之间的关系分析和模式识别。在数据分析和科学计算中，Origin软件作为一款专业的图表生成和数据处理工具，以其强大的多变量分析功能受到许多研究者的青睐。本章将首先介绍多变量分析的基本概念，然后概述Origin软件的核心功能，为后续章节深入探讨多元回归分析和主成分分析打下基础。

1.1 多变量分析的基本概念

多变量分析通常包括回归分析、主成分分析（PCA）、聚类分析等多种方法。这些技术在处理数据集时，能够揭示不同变量间的相互作用和结构关系。例如，多元回归分析可以预测因变量与多个自变量之间的依赖关系，而主成分分析则通过降维技术将复杂数据集简化，便于更好地理解数据特征。

1.2 Origin软件的核心功能

Origin软件提供了一个集成的工作环境，支持数据导入、图形绘制、数据分析和结果展示等一系列功能。它支持多种数据分析方法，并且具有直观易用的操作界面，让研究者可以快速上手。此外，Origin还支持脚本语言，可以进行自动化分析，极大地提高了分析的效率和准确性。

在接下来的章节中，我们将深入探讨如何在Origin中应用多元回归分析和主成分分析来处理实际数据问题，并通过案例来展示这些分析技术的强大应用价值。

2. 多元回归分析的理论与实践

多元回归分析是一种统计学上分析数据的方法，用于估计两个或两个以上自变量与因变量之间的关系。本章节将从理论基础讲起，详细介绍多元回归分析的构建与假设、在Origin软件中的操作步骤，以及如何解读和应用多元回归的结果。

2.1 多元回归分析基础理论

2.1.1 回归分析简介

回归分析是研究一个或多个自变量（解释变量）与因变量（响应变量）之间关系的统计方法。在多元回归中，我们可以同时考虑多个自变量对一个因变量的影响。这种方法广泛应用于预测、控制和优化问题中，例如，在经济学中预测市场需求，在医学中评估疾病与某些风险因子之间的关系。

2.1.2 多元回归模型的构建与假设

构建多元回归模型需要假设数据符合线性关系、误差项的独立性、同方差性和正态性。线性关系意味着自变量与因变量之间的关系可以用直线来近似。误差项的独立性表示数据点是随机的，没有自相关。同方差性要求误差项具有恒定的方差，正态性假设指出误差项呈正态分布。

2.2 Origin中的多元回归操作步骤

2.2.1 数据准备和导入

在Origin中进行多元回归分析之前，首先需要准备和导入数据。Origin支持多种数据格式，包括CSV、Excel等。导入数据后，需要检查数据质量，确保没有异常值或缺失值影响模型的准确性。

2.2.2 回归分析的执行与参数设定

在Origin中执行多元回归分析需要选择菜单栏中的“分析”->“回归”->“多元线性回归”。然后在弹出的对话框中选择响应变量和自变量，并设置适当的参数，例如置信区间、显著性水平等。参数设定完成后，点击“确定”进行计算。

2.3 多元回归结果的解读与应用

2.3.1 结果的统计验证

多元回归分析的结果包含了多个统计量，例如R平方、调整R平方、F值、t值等。R平方值表明了模型解释的方差比例，F值用于判断模型的整体显著性，而t值则用来评估每个自变量对因变量的影响是否显著。

2.3.2 模型的预测与优化

一旦模型被验证，它就可以用来进行预测。在Origin中，可以利用回归分析得到的模型方程进行预测，并通过添加残差分析来优化模型。残差分析能帮助识别数据中的模式，进而改善模型的准确性。

### 2.3.2.1 预测步骤
1. 在Origin中，选择“工具”->“预测”。
2. 输入需要预测的自变量值。
3. 查看预测结果和置信区间。
### 2.3.2.2 残差分析
1. 在回归结果中选择残差图。
2. 检查残差是否呈随机分布。
3. 若发现模式，可能需要调整模型或数据。

在本章中，我们从多元回归的理论基础出发，逐步深入到在Origin软件中进行多元回归分析的具体操作，并讨论了如何解读回归结果及其在实际中的应用。通过这一过程，读者应当能够理解和运用多元回归分析来解决实际问题。在下一章节，我们将转向主成分分析（PCA）的理论与实践，进一步扩展数据分析的工具箱。

3. 主成分分析的理论与实践

主成分分析（PCA）是统计学中一种降维技术，用于简化数据集，同时保留最显著的数据特征。通过PCA，我们可以将高维数据转换为低维表示，这在数据可视化、噪声过滤、特征提取及数据压缩等领域中极为有用。

3.1 主成分分析基础理论

3.1.1 主成分分析的数学原理

主成分分析是通过线性变换将原始数据变换为一组线性不相关的变量，这组新的变量称为主成分。这些主成分按照方差大小依次排列，第一个主成分具有最大的方差，第二个主成分具有次大的方差，以此类推。通过提取前几个主成分，可以在尽可能保留原始数据信息的情况下，达到降维的目的。

数学上，PCA是通过求解数据的协方差矩阵的特征值和特征向量来实现的。假设原始数据矩阵为 (X)，(X) 的协方差矩阵为 (Cov(X))，PCA的目标是找到一组正交向量 (v_1, v_2, …, v_m)，这些向量能够最大化数据在这些向量上的投影的方差。通过奇异值分解（SVD）或者特征值分解，我们可以得到这组向量，它们对应于 (Cov(X)) 的特征向量。将数据 (X) 投影到这些特征向量上，就得到了主成分。

3.1.2 数据降维的意义与方法

在数据分析过程中，高维数据往往伴随着“维数灾难”。这意味着随着数据维度的增加，数据的存储、计算和可视化变得越来越困难，而且高维数据通常存在噪声和冗余信息，这对模型的训练和解释都是不利的。数据降维是解决这些问题的有效方法之一。

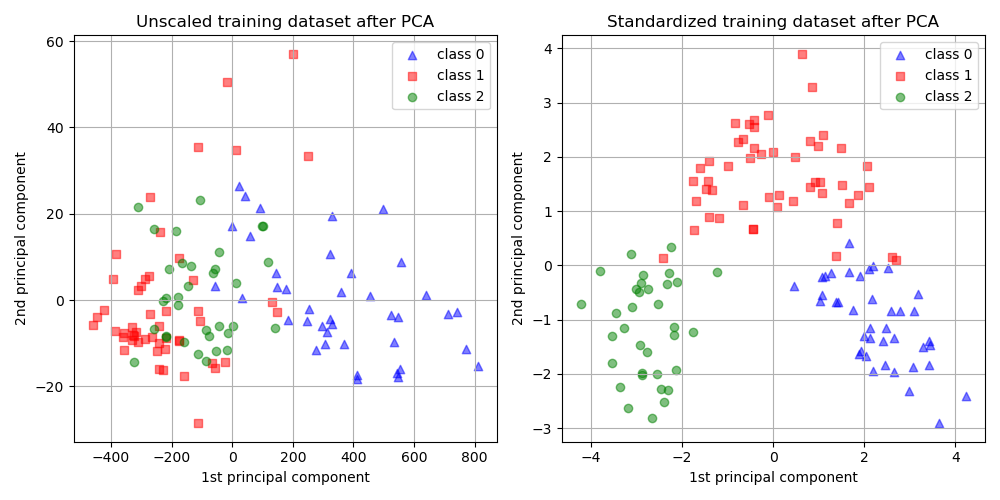
数据降维不仅能够提高计算效率和减少存储需求，还能提高数据可视化的效果，使得数据特征更加突出。例如，在多变量分析中，通过PCA降维可以将数据点投影到两维或三维空间中进行可视化。

降维的方法有很多，包括线性方法如PCA、线性判别分析（LDA）以及非线性方法如核主成分分析（Kernel PCA）、局部线性嵌入（L

最低0.47元/天解锁专栏

买1年送1年

点击查看下一篇

百万级高质量VIP文章无限畅学

千万级优质资源任意下载

C知道免费提问 ( 生成式Al产品 )

Origin多变量分析实战课：多元回归与主成分分析的深入解析

1. 多变量分析基础与Origin软件概述

1.1 多变量分析的基本概念

1.2 Origin软件的核心功能

2. 多元回归分析的理论与实践