岭回归（Ridge）分析的最新前沿：方法和应用，引领机器学习新潮流

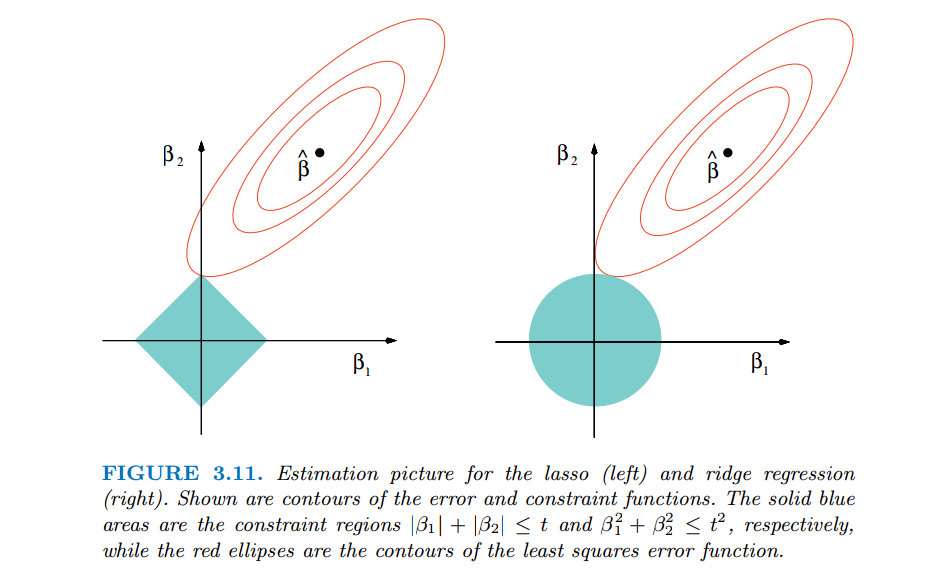
# 1. 岭回归（Ridge）分析概述

岭回归是一种正则化线性回归模型，通过在损失函数中添加一个正则化项来解决过拟合问题。它通过惩罚模型权重的大小来实现正则化，从而使模型更加稳定和鲁棒。

岭回归的损失函数由原始线性回归的平方损失和正则化项组成。正则化项是一个二次项，其系数λ控制正则化的强度。λ越大，正则化项的影响就越大，模型的权重就会越小，过拟合的风险就越低。

# 2.1 岭回归的原理和公式推导

### 2.1.1 岭回归的损失函数

岭回归的损失函数由两部分组成：

- **平方损失函数**：衡量预测值与真实值之间的差异。
- **正则化项**：惩罚模型的复杂度，防止过拟合。

岭回归的损失函数如下：

loss = (1 / 2n) * ||y - Xw||^2 + (lambda / 2) * ||w||^2

其中：

- `n` 为样本数量
- `y` 为真实值向量
- `X` 为特征矩阵
- `w` 为模型权重向量
- `lambda` 为正则化参数

### 2.1.2 岭回归的正则化项

岭回归的正则化项为 L2 范数，即权重向量的平方和。它通过惩罚权重向量的较大值来防止过拟合。

regularization_term = (lambda / 2) * ||w||^2

其中：

- `lambda` 为正则化参数

正则化参数 `lambda` 控制正则化项的强度。`lambda` 值越大，对权重向量的惩罚越大，模型越简单，过拟合的可能性越小。

### 代码逻辑分析

岭回归的损失函数通过将平方损失函数和正则化项相加来定义。平方损失函数衡量预测值与真实值之间的误差，而正则化项惩罚模型的复杂度。正则化参数 `lambda` 控制正则化项的强度，从而影响模型的复杂度和过拟合的可能性。

# 3. 岭回归的实践应用

岭回归在机器学习和数据科学领域有着广泛的应用，本章将深入探讨其在这些领域的具体实践。

### 3.1 岭回归在机器学习中的应用

**3.1.1 岭回归用于特征选择**

岭回归的正则化项可以帮助我们识别对模型预测贡献较小的特征。具体做法如下：

import numpy as np
from sklearn.linear_model import Ridge

# 加载数据
X = np.loadtxt('data.csv', delimiter=',')
y = np.loadtxt('target.csv', delimiter=',')

# 岭回归模型
model = Ridge(alpha=0.1)
model.fit(X, y)

# 获取特征权重
weights = model.coef_

# 识别低权重特征
low_weight_features = np.where(np.abs(weights) < 0.01)[0]

**3.1.2 岭回归用于模型调优**

岭回归的正则化参数α可以用来控制模型的复杂度，从而实现模型调优。具体做法如下：

# 导入必要的库
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV

# 加载数据
X = np.loadtxt('data.csv', delimiter=',')
y = np.lo