岭回归（Ridge）分析的实战案例：解决实际业务问题，提升业务价值

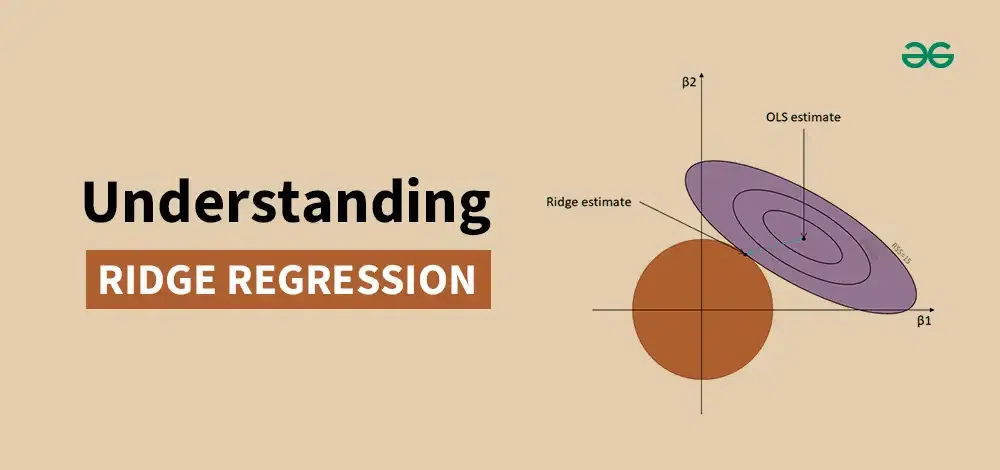
# 1. 岭回归（Ridge）分析简介

岭回归（Ridge）分析是一种正则化线性回归模型，它通过在损失函数中添加一个正则化项来解决过拟合问题。正则化项惩罚模型系数的较大值，从而使模型更加平滑，并提高其泛化能力。

岭回归模型的数学公式为：

min_w (1/2n) ||y - Xw||^2 + λ ||w||^2

其中：

* n 为样本数量
* y 为目标变量
* X 为特征矩阵
* w 为模型系数
* λ 为正则化参数

# 2. 岭回归（Ridge）分析的理论基础

### 2.1 岭回归模型的数学原理

#### 2.1.1 岭回归模型的公式推导

岭回归模型是一种线性回归模型，它在普通最小二乘法（OLS）的基础上增加了正则化项。正则化项的目的是防止模型过拟合，提高模型的泛化能力。

岭回归模型的公式如下：

min_w 1/2 * ||y - Xw||^2 + λ * ||w||^2

其中：

* y 是目标变量
* X 是自变量
* w 是模型参数
* λ 是正则化参数

正则化参数 λ 控制正则化项的强度。λ 越大，正则化项的影响越大，模型越不容易过拟合。

#### 2.1.2 岭回归模型的正则化项

岭回归模型的正则化项是 L2 范数，即参数 w 的平方和。L2 范数的目的是惩罚模型参数的较大值，防止模型过拟合。

L2 范数的数学表达式如下：

||w||^2 = w_1^2 + w_2^2 + ... + w_n^2

其中：

* w_1, w_2, ..., w_n 是模型参数

### 2.2 岭回归模型的优点和缺点

#### 2.2.1 岭回归模型的优点

* 岭回归模型可以有效防止过拟合，提高模型的泛化能力。
* 岭回归模型的求解过程是凸优化问题，可以快速求解。
* 岭回归模型对异常值不敏感，具有较好的鲁棒性。

#### 2.2.2 岭回归模型的缺点

* 岭回归模型会收缩所有模型参数，这可能会导致模型的预测精度下降。
* 岭回归模型的参数 λ 需要通过交叉验证或其他方法进行调参，这可能会增加模型训练的时间和复杂度。

# 3. 岭回归（Ridge）分析的实战应用

### 3.1 数据准备和模型训练

#### 3.1.1 数据预处理和特征工程

在进行岭回归模型训练之前，需要对数据进行预处理和特征工程，以提高模型的性能和稳定性。数据预处理包括数据清洗、缺失值处理、异常值处理和数据归一化等操作。特征工程包括特征选择、特征转换和特征组合等操作。

**数据清洗**：数据清洗的主要目的是去除数据中的噪声和错误，包括删除重复数据、处理缺失值和异常值。缺失值处理的方法有多种，如均值填充、中位数填充和插值等。异常值处理的方法也有多种，如删除异常值、Winsorize（将异常值截断在一定范围内）和标准化等。

**数据归一化**：数据归一化的目的是将不同量纲的数据映射到同一量纲，消除量纲差异对模型的影响。常用的数据归一化方法有最大-最小归一化、均值-方差归一化和标准正态分布归一化等。

**特征选择**：特征选择是选择与目标变量相关性较强、对模型预测贡献较大的特征，以减少模型的复杂度和提高模型的性能。常用的特征选择方法有过滤法、包裹法和嵌入法等。

**特征转换**：特征转换是将原始特征转换为新的特征，以提高模型的预测能力。常用的特征转换方法有独热编码、二值化、对数转换和幂次转换等。

**特征组合**：特征组合是将多个原始特征组合成新的特征，以捕获原始特征之间的交互作用。常用的特征组合方法有交叉特征、多项式特征和核函数等。

#### 3.1.2 岭回归模型