图像特征提取的基石：OpenCV SIFT算法的原理与数学基础

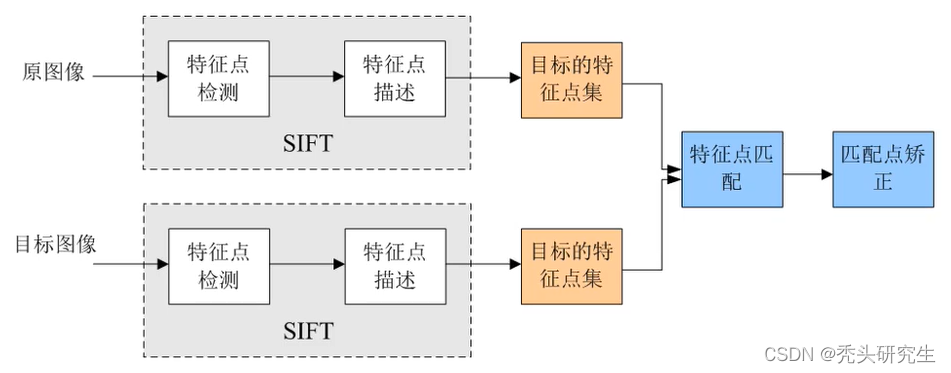
# 1. 图像特征提取概述**

图像特征提取是计算机视觉中至关重要的技术，用于从图像中提取有意义的特征，这些特征可以用于图像匹配、识别和分类等任务。SIFT（尺度不变特征变换）算法是图像特征提取中最流行和有效的算法之一，它具有尺度不变性、旋转不变性和局部不变性等优点。

SIFT算法的基本原理是通过检测图像中的关键点（特征点），并计算这些关键点的描述符。关键点是图像中具有显著变化的点，通常对应于图像中的角点、边缘和斑点等特征。描述符是关键点的局部特征，它可以描述关键点的形状、大小和方向等信息。通过计算关键点的描述符，我们可以对图像进行匹配和识别。

# 2. SIFT算法原理

### 2.1 尺度空间极值检测

SIFT算法的核心思想是通过在不同尺度空间中检测图像中的特征点，并对这些特征点进行描述。尺度空间极值检测是SIFT算法的第一步，其目的是找到图像中在不同尺度上都具有稳定响应的特征点。

**步骤：**

1. **构建高斯金字塔：**将原始图像缩小到不同尺度，形成高斯金字塔。每个尺度上的图像称为一个octave。
2. **计算差分图像：**对每个octave的图像进行高斯差分，得到差分图像。
3. **寻找极值点：**对每个差分图像，在相邻的尺度和空间位置上比较像素值，找到局部极值点。

**代码示例：**

import cv2

# 构建高斯金字塔
img = cv2.imread('image.jpg')
octaves = cv2.buildGaussianPyramid(img, 3)

# 计算差分图像
diff_images = []
for octave in octaves:
    diff_images.append(cv2.Laplacian(octave, cv2.CV_32F))

# 寻找极值点
keypoints = []
for diff_image in diff_images:
    keypoints.extend(cv2.goodFeaturesToTrack(diff_image, 1000, 0.01, 10))

**逻辑分析：**

* `cv2.buildGaussianPyramid`函数将图像缩小到不同尺度，形成高斯金字塔。
* `cv2.Laplacian`函数计算差分图像。
* `cv2.goodFeaturesToTrack`函数寻找局部极值点。

### 2.2 方向分配

尺度空间极值检测得到的特征点是无方向的。为了使特征点具有旋转不变性，需要为每个特征点分配一个方向。

**步骤：**

1. **计算梯度直方图：**在特征点周围的邻域内计算图像梯度，并统计不同方向上的梯度值。
2. **找到主方向：**将梯度直方图中最大的峰值对应的方向作为特征点的方向。

**代码示例：**

# 计算梯度直方图
hist = cv2.calcHist([img], [0], None, [36], [0, 360])

# 找到主方向
max_value = np.max(hist)
max_index = np.argmax(hist)
orientation = max_index * 10

**逻辑分析：**

* `cv2.calcHist`函数计算梯度直方图。
* `np.max`函数找到梯度直方图中的最大值。
* `np.argmax`函数找到梯度直方图中最大值对应的方向。

### 2.3 特征描述

特征描述是SIFT算法的关键步骤，其目的是为每个特征点生成一个唯一的描述符，以用于匹配和识别。

**步骤：**

1. **构建特征描述窗口：**在特征点周围以主方向为中心建立一个窗口。
2. **计算梯度直方图：**在窗口内计算图像梯度，并统计不同方向上的梯度值。
3. **归一化和量化：**将梯度直方图归一化到单位长度，并量化为8个bin。
4. **连接描述符：**将每个bin的梯度值连接成一个向量，作为特征描述符。

**代码示例：**

# 构建特征描述窗口
descriptor = np.zeros((128,))
for i in range(4):
    for j in range(4):
        x = int(feature.pt[0] + i * step)
        y = int(feature.pt[1] + j * step)
        hist = cv2.calcHist([img], [0], None, [8], [0, 360], mask=mask)
        descriptor[i * 4 + j] = np.max(hist)

# 归一化和量化
descriptor = descriptor / np.linalg.norm(descriptor)
descriptor = np.round(descr