MATLAB机器人工具箱中的先进运动规划算法：探索机器人运动的极限

# 1. MATLAB机器人工具箱简介**

MATLAB机器人工具箱是一个强大的工具包，为机器人学研究和开发提供了全面的功能。它提供了用于机器人运动规划、控制、仿真和可视化的函数和工具。

该工具箱包括用于路径规划和运动规划的算法，例如狄克斯特拉算法、A*算法、RRT、RRT*和PRM。它还提供了用于控制机器人的函数，例如PID控制器、状态空间控制器和模型预测控制器。此外，该工具箱还包括用于仿真和可视化机器人的工具，例如Simulink和Robotics System Toolbox。

# 2. 机器人运动规划理论

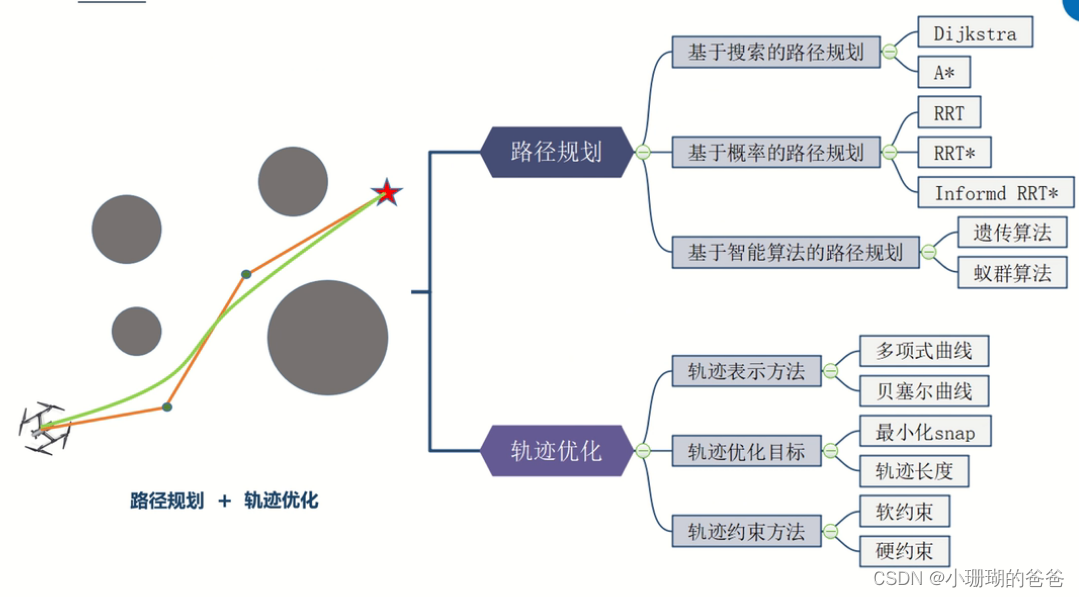
### 2.1 路径规划

路径规划是在给定的环境中，为机器人寻找一条从起点到终点的无碰撞路径。它通常被分解为以下两个子问题：

- **可视化环境：**将环境表示为一个图或其他数据结构，其中节点表示可行的机器人位置，边表示连接这些位置的路径。
- **搜索算法：**使用搜索算法（如狄克斯特拉或 A*）在图中找到从起点到终点的最优路径。

#### 2.1.1 狄克斯特拉算法

狄克斯特拉算法是一种贪心算法，它从起点开始，逐步扩展搜索范围，直到找到一条到终点的路径。其算法步骤如下：

function dijkstra(graph, start, end)
    // 初始化距离和父节点字典
    distance[start] = 0
    for node in graph:
        if node != start:
            distance[node] = infinity
            parent[node] = null

    // 优先队列，按距离排序
    Q = priority_queue(graph)

    // 主循环
    while Q not empty:
        u = Q.pop()
        if u == end:
            break
        for v in graph[u]:
            alt = distance[u] + graph[u][v]
            if alt < distance[v]:
                distance[v] = alt
                parent[v] = u

    // 重建路径
    path = []
    current = end
    while current != start:
        path.append(current)
        current = parent[current]
    path.reverse()
    return path

**参数说明：**

- `graph`：表示环境的图
- `start`：起点
- `end`：终点

**代码逻辑分析：**

1. 初始化距离和父节点字典，将起点距离设为 0，其他节点距离设为无穷大。
2. 创建一个优先队列，按距离排序。
3. 主循环从优先队列中弹出距离最小的节点 `u`。
4. 遍历节点 `u` 的所有邻居 `v`。
5. 计算从起点到 `v` 的替代距离 `alt`。
6. 如果 `alt` 小于 `v` 的当前距离，则更新 `v` 的距离和父节点。
7. 当 `u` 为终点时，退出循环。
8. 重建路径，从终点回溯到起点。

#### 2.1.2 A*算法

A*算法是一种启发式搜索算法，它结合了狄克斯特拉算法和贪心搜索。它使用启发函数来估计从当前节点到终点的距离，并优先搜索估计距离最小的节点。

function a_star(graph, start, end)
    // 初始化距离和父节点字典
    g_score[start] = 0
    f_score[start] = g_score[start] + h(start, end)
    for node in graph:
        if node != start:
            g_score[node] = infinity
            f_score[node] = infinity
            parent[node] = null

    // 优先队列，按 f_score 排序
    Q = priority_queue(graph)

    // 主循环
    while Q not empty:
        u = Q.pop()
        if u == end:
            break
        for v in graph[u]:
            alt = g_score[u] + graph[u][v]
            if alt < g_score[v]:
                g_score[v] = alt
                f_score[v] = g_score[v] + h(v, end)
                parent[v] = u

    // 重建路径
    path = []
    current = end
    while current != start:
        path.append(current)
        current = parent[current]
    path.reverse()
    return path

**参数说明：**

- `graph`：表示环境的图
- `start`：起点
- `end`：终点
- `h(node, end)`：启发函数，估计从 `node` 到 `end` 的距离

**代码逻辑分析：**

1. 初始化距离和父节点字典，将起点距离设为 0，其他节点距离设为无穷大。
2. 创建一个优先队列，按 f_score 排序。
3. 主循环从优先队列中弹出 f_score 最小的节点 `u`。
4. 遍历节点 `u` 的所有邻居 `v`。
5. 计算从起点到 `v` 的替代距离 `alt`。
6. 如果 `alt` 小于 `v` 的当前距离，则更新 `v` 的距离和父节点。
7. 当 `u` 为终点时，退出循环。
8. 重建路径，从终点回溯到起点。

### 2.2 运动规划

运动规划是在给定的环境中，为机器人寻找一条从起点到终点的无碰撞路径，同时考虑机器人的运动学约束。它通常涉及以下步骤：

- **机器人建模：**建立机器人的运动学模型，描述其运动范围和约束。
- **障碍物建模：**识别环境中的障碍物并将其表示为几何形状。
- **运动规划算法：**使用运动规划算法（如 RRT、RRT* 或 PRM）在考虑机器人约束和障碍物的情况下，找到一条可行的路径。

#### 2.2.1 随机采样运动规划（RRT）

RRT算法是一种基于随机采样的运动规划算法。其算法步骤如下：

function rrt(robot, environment, start, goal)
    // 初始化树
    tree = {start}

    // 主循环
    while true:
        // 随机采样一个点
        q_rand = sample_free()

        // 找到树中离 q_rand 最近的点
        q_nearest = nearest_neighbor(tree, q_rand)

        // 向 q_rand 方向扩展树
        q_new = steer(q_nearest, q_rand)

        // 如果 q_new 有效（无碰撞）
        if is_valid(q_new):
            tree.add(q_new)

        // 如果 q_new 接近目标
        if is_close(q_new, goal):
            break

    // 重建路径
    path = []
    current = q_new
    while current != start:
        path.append(current)
        current = parent[current]
    path.reverse()
    return path

**参数说明：**

- `robot`：机器人的运动学模型
- `environment`：环境模型
- `start`：起点
- `goal`：终点

**代码逻辑分析：**

1. 初始化树，将起点加入树中。
2. 主循环不断随机采样一个点，并找到树中离该点最近的点。
3. 向采样点方向扩展树，如果扩展后的点有效，则将其加入树中。
4. 当扩展后的点接近目标时，退出循环。
5. 重建路径，从目标点回溯到起点。

#### 2.2.2 快速扩展随机树（RRT*）

RRT*算法是对 RRT 算法的改进，它使用启发式函数来指导搜索过程。其算法步骤如下：

function rrt_star(robot, environment, start, goal)
    // 初始化树
    tree = {start}

    // 主循环
    while true:
        // 随机采样一个点
        q_rand = sample_free()

        // 找到树中离 q_rand 最近的点
        q_nearest = nearest_neighbor(tre