【系统级设计挑战】：Sigma-Delta ADC全局视角下的策略与考量


# 摘要
Sigma-Delta模数转换器（ADC）是一种高精度、高分辨率的转换技术，在信号处理领域占据重要地位。本文首先介绍了Sigma-Delta ADC的基本概念及其设计理论基础，包括过采样、噪声整形、量化噪声和滤波器设计等方面。随后，文章探讨了Sigma-Delta ADC的实际设计过程，包括版图布局、模拟前端电路设计和数字后端处理等关键步骤。接着，文章对Sigma-Delta ADC的测试与评估进行了详述，涉及性能测试标准、问题诊断及解决方案，并与传统ADC技术进行了比较分析。最后，文章讨论了Sigma-Delta ADC在新兴应用中的创新实践，如物联网、高精度测量控制以及智能化和自动化设计趋势。本文旨在为读者提供全面的Sigma-Delta ADC技术知识和实际应用指导。

# 关键字
Sigma-Delta ADC；过采样；噪声整形；量化噪声；滤波器设计；系统级设计；性能测试；物联网应用

参考资源链接：[高速CT Sigma-Delta ADC设计：5MHz带宽，63.6 dB SNR，低功耗](https://wenku.csdn.net/doc/64562ac695996c03ac16e28f?spm=1055.2635.3001.10343)
# 1. Sigma-Delta ADC的基本概念

Sigma-Delta模数转换器（ADC）是现代电子系统中不可或缺的一部分，其在处理低频信号方面表现出色，特别是在音频和仪表系统中。相较于传统的Nyquist速率ADC，Sigma-Delta ADC通过过采样和噪声整形技术来提高转换精度和分辨率。其核心思想在于将信号的量化噪声转移到高频区域，从而在感兴趣的频带内保留了较高的信号质量。这些ADCs通常用于需要高分辨率和低噪声性能的场合，例如高保真音频设备和精密测量仪器。在了解其工作原理之前，我们先来探讨一下它的基本架构和工作流程。

# 2. Sigma-Delta ADC的设计理论基础

## 2.1 过采样和噪声整形技术

### 2.1.1 过采样的原理及其对信号的影响

过采样是Sigma-Delta ADC设计中的一项关键技术，通过在一个较高的采样率下采样输入信号，以增加信号的分辨率并降低量化噪声。与传统的Nyquist速率采样相比，过采样技术可以将量化噪声能量平均分散到更宽的频率范围内，从而在感兴趣的信号频带内减少量化噪声的幅度。

过采样原理的核心是依据奈奎斯特采样定理，采样频率必须至少是信号最高频率的两倍，以避免混叠。在Sigma-Delta ADC中，通过提高采样频率，可以将量化噪声推至更高的频率，然后利用一个低通滤波器来滤除这部分高频噪声。例如，若原始信号带宽为fB，则过采样率为L意味着采样频率fs为2fB*L，使得量化噪声主要集中在fs/2至fs/2之间的频带，远高于信号带宽。

### 2.1.2 噪声整形的数学模型和效果分析

噪声整形技术则进一步利用一个环路滤波器（通常为一个低通滤波器）在信号的高频部分增加噪声。该技术通过在信号处理路径中引入反馈，将量化噪声的功率谱转移到更高的频率范围内，从而在信号带宽内实现更低的噪声水平。

噪声整形过程通常由一个数字积分器和一个数字或模拟滤波器组成。积分器将量化误差积分起来，并通过反馈机制重新加入到模拟信号中。这样，量化噪声就被推到了高频区域。数学上，噪声整形效果可以通过传递函数来描述，比如一个一阶噪声整形器的传递函数可以表示为：

\[ H(z) = 1 - (1 - z^{-1})^N \]

这里N是噪声整形器的阶数。对于一阶噪声整形器，N为1，输出信号的噪声谱会呈现出一个从DC到fs/2的一阶下降趋势。

## 2.2 模数转换的量化噪声和滤波器设计

### 2.2.1 量化噪声的来源及其特性

量化噪声源于模拟信号到数字信号转换过程中不可避免的舍入误差。在数字域中，由于位数的限制，真实世界连续变化的信号只能被离散地表示，这导致了信号和其数字表示之间的差异。当信号被采样和量化时，这种差异表现为误差，即量化噪声。量化噪声的大小与量化器的位数成反比，位数越多，量化噪声越小，信号的精度越高。

量化噪声可以视为一种均匀分布的白噪声，其功率谱密度（PSD）在信号带宽内是常数。理论上，量化噪声的总功率为：

\[ P_{\text{quantization}} = \frac{\Delta^2}{12} \]

其中，\(\Delta\)是量化步长，对于满量程为VREF的信号，\(\Delta = \frac{VREF}{2^N}\)，N是ADC的位数。

### 2.2.2 滤波器设计的基本要求和常见结构

在Sigma-Delta ADC中，滤波器的主要作用是抑制量化噪声，使其远离信号频带。为了实现这一目的，滤波器需要具备良好的选择性，即在信号带宽内提供平坦的增益，而在带外迅速下降到零。

根据所需的性能和设计复杂性，可以采用不同类型的滤波器结构。常见的有FIR（有限脉冲响应）和IIR（无限脉冲响应）滤波器。Sigma-Delta ADC通常使用的是IIR滤波器，特别是Sinc滤波器。Sinc滤波器具有很深的衰减和良好的阻带特性，但它们的线性相位和稳定性可能难以保证。此外，由于IIR滤波器在反馈环节引入了延迟，因此必须特别注意其稳定性问题。

FIR滤波器的一个优点是具有绝对的稳定性和线性相位响应，但它可能需要更多的延迟和更高的阶数来达到所需的滤波性能，这在实际硬件实现中会带来挑战。

## 2.3 系统级设计的关键参数考量

### 2.3.1 信号带宽和动态范围

信号带宽定义了ADC处理信号的频率范围。在Sigma-Delta ADC中，过采样和噪声整形技术允许设计者以牺牲更高的采样频率为代价来获得较宽的信号带宽。但是，增加采样频率会导致数据处理量的增加，因此需要在信号带宽、动态范围和功耗之间做出权衡。

动态范围是ADC能够分辨最小信号与最大信号幅度的范围，通常以分贝（dB）为单位表示。动态范围越大，ADC在处理小信号和大信号时的性能越好。在Sigma-Delta ADC中，动态范围直接受到量化噪声和过采样比率的影响。

### 2.3.2 信噪比(SNR)和总谐波失真(THD)

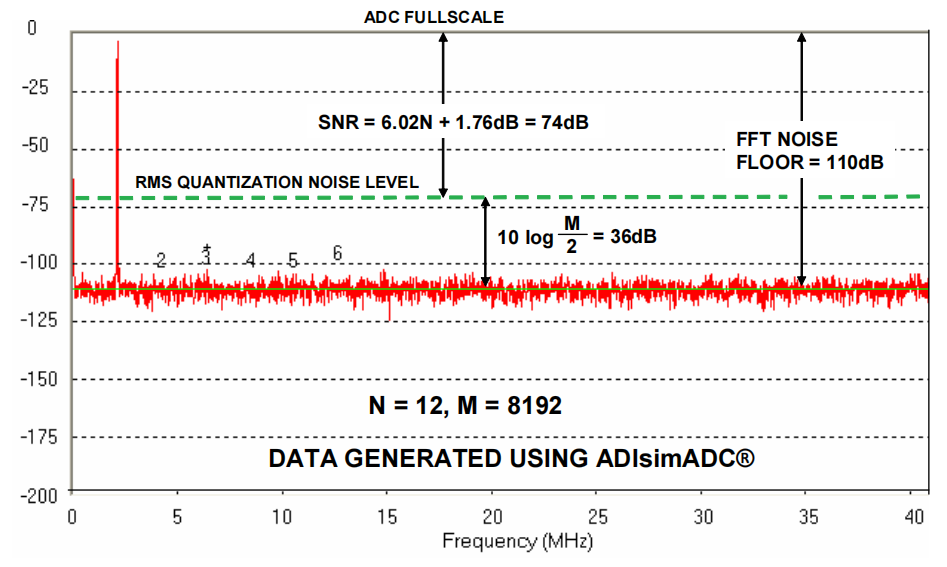
信噪比（Signal-to-Noise Ratio, SNR）是衡量ADC性能的重要指标，反映了信号功率与噪声功率的比值。对于一个理想的ADC，SNR可以通过以下公式计算：

\[ SNR = 6.02N + 1.76dB \]

其中N是ADC的分辨率。对于Sigma-Delta ADC，由于过采样和噪声整形技术的应用，其实际SNR通常会高于这个理论值。

总谐波失真（Total Harmonic Distortion, THD）指的是信号中所有谐波分量相对于基频信号的功率比值。THD低意味着信号失真小，能够提供更高的保真度。在Sigma-Delta ADC中，THD会受到滤波器设计、过采样率和量化噪声的影响。

# 3. Sigma-Delta ADC的实际