【Sigma-Delta ADC性能优化】：反馈与前馈滤波器设计的精髓


# 摘要
Sigma-Delta模数转换器（ADC）因其高分辨率和高信噪比（SNR）而广泛应用于数据采集和信号处理系统中。本文首先概述了Sigma-Delta ADC性能优化的重要性及其基本原理，随后重点分析了反馈和前馈滤波器的设计与优化，这两者在提高转换器性能方面发挥着关键作用。文中详细探讨了滤波器设计的理论基础、结构设计和性能优化策略，并对Sigma-Delta ADC在系统级的优化进行了深入分析。此外，本文还探讨了校准技术对提升系统性能的重要性。最后，文章展望了Sigma-Delta ADC的未来发展趋势，讨论了新技术对其性能优化的潜在影响，以及未来技术趋势和行业需求。

# 关键字
Sigma-Delta ADC；性能优化；反馈滤波器；前馈滤波器；系统级优化；校准技术

参考资源链接：[高速CT Sigma-Delta ADC设计：5MHz带宽，63.6 dB SNR，低功耗](https://wenku.csdn.net/doc/64562ac695996c03ac16e28f?spm=1055.2635.3001.10343)
# 1. Sigma-Delta ADC性能优化概述

Sigma-Delta模数转换器（ADC）凭借其在高精度和低噪声性能方面的独特优势，在多种应用场合中得到广泛应用。优化Sigma-Delta ADC的性能，不仅可以提高其在信号处理中的应用质量，而且能够带来功耗、成本和设计复杂度的优化。

## 1.1 ADC性能优化的动机

在许多高精度要求的领域，例如医疗设备、音频录制、通信系统等，对ADC的性能要求非常高。为了满足这些应用的精度需求，优化Sigma-Delta ADC的性能成为设计者的一项重要任务。性能优化不仅提升了系统的整体性能，还能在某些情况下减少对后端数字信号处理的依赖，实现更高效的系统设计。

## 1.2 优化的方法论

对Sigma-Delta ADC进行性能优化，涉及的方法论广泛而深入，从电路设计到系统集成，从材料选择到信号处理算法。这些方法可以大致分为：电路层面的优化，包括滤波器设计、采样频率调整等；系统层面的优化，如噪声抑制、功耗管理以及高级数字校准技术的实现等。本章将对这些方法论进行概述，并在后续章节中详细探讨。

# 2. Sigma-Delta ADC的基本原理

Sigma-Delta模数转换器（ADC）在高精度数据采集和信号处理领域中占据重要地位。它的核心优势在于能够实现高分辨率的同时保持较低的功耗。为了深入了解Sigma-Delta ADC的性能优化，首先必须理解其基本原理。

## 2.1 模数转换的背景与需求

### 2.1.1 模拟信号和数字信号的转换基础

模拟信号是指连续变化的信号，它可以在时间和幅度上取任意值。而数字信号则是一系列离散值的集合，这些值通常由二进制数表示。模数转换（Analog-to-Digital Conversion, ADC）是将连续的模拟信号转换为离散的数字信号的过程。

模拟信号通常是由自然界中的物理量（如温度、压力、声音等）通过传感器转化为电信号。数字信号则广泛应用于计算机处理和通信系统中，因为它们更容易存储、处理和传输。

ADC转换过程通常包含以下几个步骤：
1. 采样（Sampling）：将连续的模拟信号在特定的时间点上进行采样。
2. 量化（Quantization）：将采样后的信号幅度转化为有限数量的离散值。
3. 编码（Encoding）：将量化后的信号值转换为二进制代码。

### 2.1.2 模数转换的应用场景和要求

模数转换在多个行业领域中有广泛应用，例如：
- 音频处理：在音乐制作和播放设备中，将麦克风捕捉的模拟声音信号转换为数字信号进行处理。
- 通信系统：在移动通信、卫星通信中，通过ADC将接收到的模拟信号转换为数字信号进行解调和解码。
- 医疗设备：如心电图、MRI等设备中，将生物电信号转换为数字信号进行记录和分析。
- 自动化和控制：工业传感器、机器人等设备中，将物理信号转换为数字信号进行进一步的处理和控制。

在应用中，对ADC性能的需求包括高分辨率（即高精度）、高动态范围、低噪声、低功耗等。随着技术的发展，还出现了更多特殊要求，比如高速率转换、抗抖动性能等。

## 2.2 Sigma-Delta ADC的工作机制

### 2.2.1 过采样和噪声整形技术

Sigma-Delta ADC的工作原理与传统的逐次逼近型ADC和闪速ADC等不同，它采用了过采样（Oversampling）和噪声整形（Noise Shaping）的技术。

过采样是指在模数转换过程中，采样率远高于奈奎斯特频率（Nyquist Rate，即信号最高频率的两倍）。例如，对于一个4kHz的音频信号，按照奈奎斯特定理，至少需要8kHz的采样率，但Sigma-Delta ADC可能会采用数十甚至数百kHz的采样率。

噪声整形技术则是利用反馈机制将量化噪声转移到高于信号带宽的频率范围内，这样就可以在后续的数字滤波过程中轻松去除噪声，而不影响信号的质量。

### 2.2.2 Sigma-Delta调制器的组成和原理

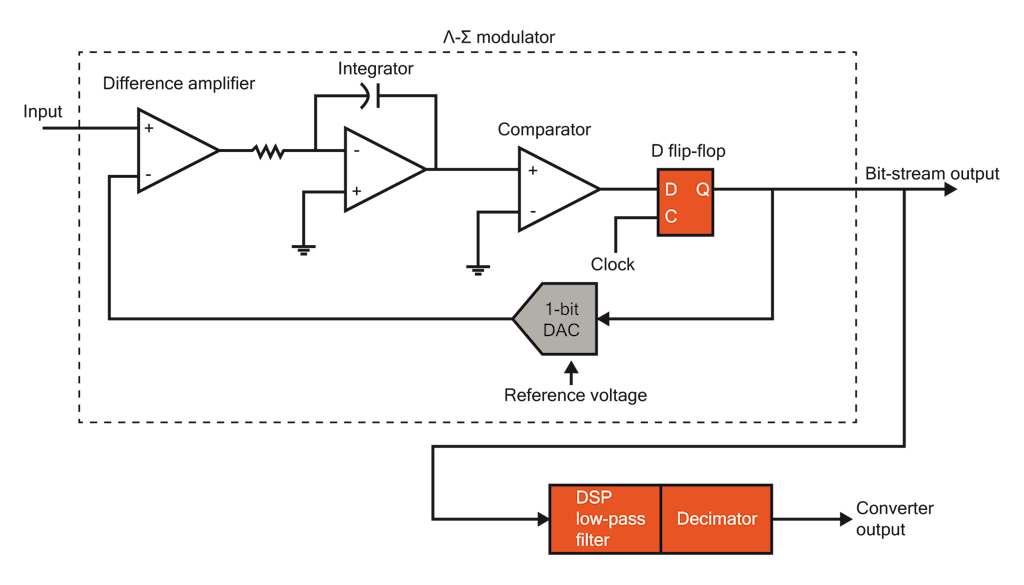
Sigma-Delta调制器是Sigma-Delta ADC的核心组件，它通过引入反馈回路和差分器、积分器以及1位量化器的级联结构实现信号的调制。

- 差分器（Differencer）：计算输入信号与反馈信号之间的差值。
- 积分器（Integrator）：将差分器输出的信号进行积分，形成累加误差。
- 量化器（Quantizer）：将积分器的输出转换为1位数字信号，通常为高或低电平。
- 反馈回路（Feedback Loop）：将量化器的输出反馈到差分器的输入端，形成一个闭环系统。

这个调制过程不断地迭代，产生了包含信息和噪声的1位数据流。随后，这个数据流通过数字低通滤波器进行处理，滤除高频噪声，从而恢复出高质量的数字信号。

## 2.3 Sigma-Delta ADC的关键性能指标

### 2.3.1 信噪比(SNR)和动态范围

信噪比（Signal-to-Noise Ratio, SNR）是衡量ADC性能的重要指标，它定义为信号功率与噪声功率的比值。高SNR意味着信号中包含的噪声较少，信号更加清晰。

动态范围是指ADC能够处理的最大信号强度与最小信号强度之间的比值。一个较高的动态范围表示ADC可以准确地处理从极小到极大的信号变化，这对于捕捉微弱信号和大动态范围的场景特别重要。

### 2.3.2 总谐波失真(THD)和无杂散动态范围(SFDR)

总谐波失真（Total Harmonic Distortion, THD）衡量的是信号中谐波失真成分的大小，谐波失真通常由非线性失真造成。THD越低，表明信号失真越小，声音等模拟信号转换后的保真度越高。

无杂散动态范围（Spurious-Free Dynamic Range, SFDR）是指在ADC输出信号中，除了基波信号外，功率最大的谐波或杂散信号与基波信号之间的比值。较高的SFDR意味着在信号中出现的杂散信号较弱，这在无线通信等领域非常重要。

在本章中，我们探讨了Sigma-Delta ADC的基本原理，包括其在模数转换中的应用背景与需求，工作机制中的过采样与噪声整形技术，以及调制器的组成原理。后续章节将深入探讨反馈滤波器和前馈滤波器的设计与优化，以及Sigma-Delta ADC在系统级别的优化策略和未来发展趋势。

# 3. 反馈滤波器设计与优化

## 3.1 反馈滤波器的理论基础

### 3.1.1 滤波器的基本概念和作用

滤波器是信号处理领域中的核心组件，其主要功能是允许特定频率范围内的信号通过，同时抑制或滤除其它频率的信号。在Sigma-Delta模数转换器（ADC）中，反馈