【金融分析的数学武器】：Isserlis' Theorem 在市场预测中的创新使用


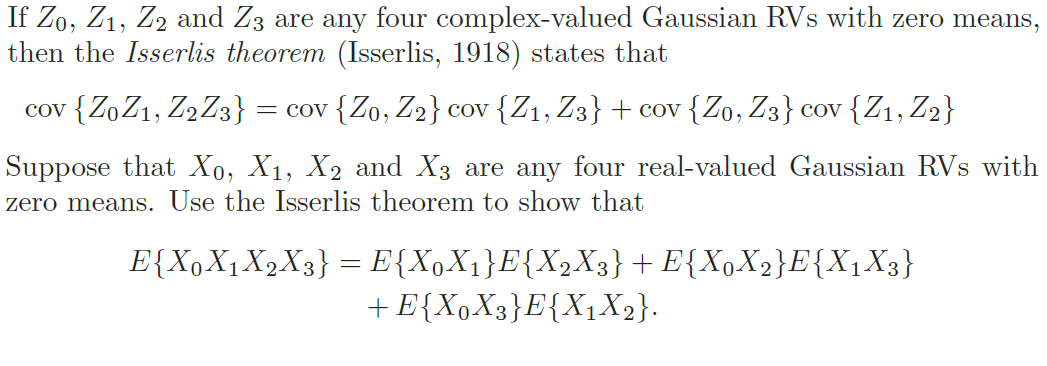
参考资源链接：[Isserlis定理：多元正态分布任意阶混合矩的通用公式证明](https://wenku.csdn.net/doc/6tpi5kvhfa?spm=1055.2635.3001.10343)
# 1. Isserlis' Theorem 简介及其数学基础

## 1.1 Isserlis' Theorem 的起源和意义

Isserlis' Theorem，又称为多元正态分布矩生成函数的特征，是数理统计学中一个较为重要的定理。其以英国数学家列奥·伊斯塞利斯的名字命名，于1918年首次发表。该定理为计算多元正态分布随机变量的联合矩提供了简洁的表达方式，对于多元统计分析和金融领域的风险评估具有重要的应用价值。

## 1.2 Isserlis' Theorem 数学表述

从数学的角度来看，Isserlis' Theorem 可以表述为：给定一组标准正态分布的独立随机变量 \(X_1, X_2, ..., X_n\)，其二阶矩和四阶矩可以表示为：
\[ E[X_1 X_2 X_3 X_4] = E[X_1 X_2]E[X_3 X_4] + E[X_1 X_3]E[X_2 X_4] + E[X_1 X_4]E[X_2 X_3] \]

这个定理说明了在多元正态分布的情况下，随机变量的四阶矩可以通过其二阶矩（即协方差）的组合来表示。在应用中，这个特性可以大大简化高维数据分析的复杂性。

## 1.3 Isserlis' Theorem 的基础数学概念

了解Isserlis' Theorem 的基础概念需要熟悉多元正态分布以及矩的定义。正态分布是统计学中非常常见的分布形式，而矩则是描述随机变量分布特征的数值指标。Isserlis' Theorem 是基于这两个概念的深入探讨，它揭示了在特定条件下，高阶矩如何依赖于低阶矩，从而为统计推断提供了坚实的理论基础。

在接下来的章节中，我们将深入探讨Isserlis' Theorem 在金融分析中的具体应用，以及它在理论和实践中所扮演的关键角色。

# 2. Isserlis' Theorem 在金融分析中的理论应用

金融分析领域中，Isserlis' Theorem（伊瑟利斯定理）为高阶统计矩的计算提供了理论基础。理解该定理不仅有助于深入研究金融市场中资产的统计特性，而且在市场风险评估和资产组合优化中也占有重要地位。本章节将探讨Isserlis' Theorem的基本概念，阐述其在统计学中的角色，并进一步讨论在市场预测中的应用。

## 2.1 Isserlis' Theorem 的基本概念

### 2.1.1 定理的历史背景

Isserlis' Theorem是由数学家Leonard Henry Caleb Isserlis提出的，最初出现在1918年的一篇论文中。该定理最初是为了解决物理学中相关随机变量的高阶矩问题。而在金融领域，该定理提供了一种计算多元正态分布随机变量乘积矩的方法。

### 2.1.2 定理的数学表述

在数学上，Isserlis' Theorem可以表述为：对于具有零均值的多元正态分布随机变量 \(X_1, X_2, ..., X_n\)，它们的4阶矩可以通过以下公式计算：

\[E[X_1X_2X_3X_4] = E[X_1X_2]E[X_3X_4] + E[X_1X_3]E[X_2X_4] + E[X_1X_4]E[X_2X_3]\]

该定理可以扩展到更高阶的矩，但计算复杂度会显著增加。

## 2.2 Isserlis' Theorem 在统计学中的角色

### 2.2.1 高阶矩的计算

金融时间序列的分析常常需要利用到高阶矩，例如偏度（skewness）和峰度（kurtosis）。Isserlis' Theorem提供了一种在多元正态分布假设下的计算途径，简化了高阶矩的计算过程。

### 2.2.2 多变量正态分布的性质

在金融领域，许多资产收益率的分布往往被假定为正态分布。Isserlis' Theorem不仅帮助我们计算复杂的乘积矩，而且有助于我们更好地理解这些资产收益率之间的相关结构及其联合分布的特性。

## 2.3 Isserlis' Theorem 在市场预测中的初步运用

### 2.3.1 市场风险评估

市场风险评估通常涉及对资产价格波动性的衡量，这需要计算诸如方差和协方差等二阶矩，甚至是偏度和峰度等高阶矩。Isserlis' Theorem对于这些高阶矩的计算提供了直接帮助，从而影响风险的量化模型，如风险价值(Value at Risk, VaR)和预期短缺(Conditional Value at Risk, CVaR)。

### 2.3.2 资产组合优化

在资产组合优化中，Isserlis' Theorem可以被用来计算资产收益率的协方差矩阵，这对于有效前沿(Efficient Frontier)的计算至关重要。资产组合管理者利用这些高阶矩信息可以更好地构建风险和收益平衡的资产组合。

graph TD
    A[开始] --> B[确定资产组合]
    B --> C[计算资产收益的均值和协方差]
    C --> D[使用Isserlis' Theorem计算高阶矩]
    D --> E[构建优化模型]
    E --> F[计算有效前沿]
    F --> G[调整资产权重]
    G --> H[最终资产组合配置]
    H --> I[结束]

在上述流程中，Isserlis' Theorem是一个关键步骤，确保了高阶统计矩的精确计算，从而影响到整个资产组合优化的结果。

代码块示例：

import numpy as np

# 假设X1, X2, X3, X4是具有零均值的多元正态分布随机变量
def isselis_theorem(x1, x2, x3, x4):
    E_X1X2 = np.mean(x1 * x2)
    E_X1X3 = np.mean(x1 * x3)
    E_X1X4 = np.mean(x1 * x4)
    E_X2X3 = np.mean(x2 * x3)
    E_X2X4 = np.mean(x2 * x4)
    E_X3X4 = np.mean(x3 * x4)
    E_X1X2X3X4 = (E_X1X2 * E_X3X4) + (E_X1X3 * E_X2X4) + (E_X1X4 * E_X2X3)
    return E_X1X2X3X4

# 示例代码段演示了如何使用Isserlis' Theorem来计算四个随机变量的4阶矩。

通过上述代码，我们可以看到如何在实践中应用Isserlis' Theorem来计算多元正态分布随机变量的4阶矩。在每个步骤中，我们通过`numpy`库中的`mean`函数来计算变量的期望值，最终根据Isserlis' Theorem的公式计