【计算机组成原理中的数据表示】：理解二进制与编码，构建稳固的数据基础

目录
摘要
关键字
1. 计算机组成原理概述
2. ```
第二章：二进制基础与数制转换

2.1 二进制数制的原理与特点

2.1.1 二进制数制的定义
2.1.2 二进制数制的应用场景

2.2 二进制数制与其他数制的转换

2.2.1 二进制与十进制的转换方法
2.2.2 二进制与十六进制的转换方法

2.3 二进制运算规则与应用实例

2.3.1 基本的二进制运算规则
2.3.2 二进制运算在计算机中的应用实例

解锁专栏，查看完整目录
摘要
本文全面介绍了计算机组成原理，深入探讨了二进制基础及其与其它数制的转换方法。文章阐述了二进制数制的原理、特点及其在计算机中的应用场景，同时分析了不同数制转换的技术细节和实际应用。数据表示与编码技术章节着重讲解了字符、数字和指令的数据表示，字符编码标准，以及浮点数的表示方法和标准。在数据编码的高级应用中，探讨了错误检测与校正码、数据压缩技术以及编码理论在数据安全中的应用。最后一章通过实践活动，强调了数制转换、编码技术应用及数据表示方案分析和优化的重要性。本文旨在为读者提供一套完整的计算机基础理论知识框架和实际操作指导。
关键字
计算机组成原理；二进制数制；数制转换；数据表示；编码技术；浮点数标准；错误检测校正码；数据压缩；数据安全；实践应用
参考资源链接：计算机组成原理复习与知识点详解
1. 计算机组成原理概述
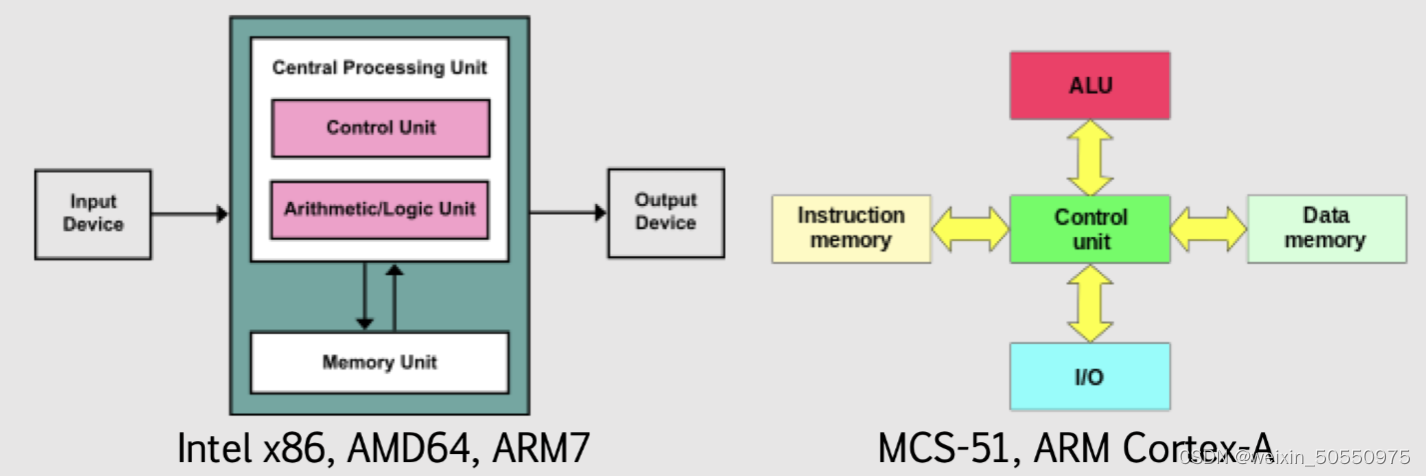
计算机作为现代社会不可或缺的工具，其工作原理始终是技术发展中的核心。第一章将为大家揭开计算机组成原理的神秘面纱，探讨其基础结构和核心工作流程。我们将从宏观上理解计算机硬件和软件如何协同工作，以及计算机的五大基本组成部分：运算器、控制器、存储器、输入设备和输出设备。此外，本章还会介绍计算机的处理流程，包括数据的输入、处理、存储和输出，以及这些过程是如何相互作用实现复杂计算任务的。通过本章的介绍，读者将能够建立起计算机工作的初步概念，为深入学习后续章节打下坚实的基础。
2. ```
第二章：二进制基础与数制转换
2.1 二进制数制的原理与特点
2.1.1 二进制数制的定义
二进制数制是一种使用两个符号（通常为0和1）来表示数值的数制系统。它在现代计算机科学和信息技术中占有基础地位，因为计算机内部所有的处理都是基于二进制系统完成的。二进制的每个位置代表一个固定的权重值，权重值是2的幂次方，从右向左依次为2的0次方、2的1次方、2的2次方，以此类推。
2.1.2 二进制数制的应用场景
二进制的应用场景非常广泛，几乎所有电子设备的核心电路都以二进制为基础。从最初的逻辑门电路、寄存器、微处理器到复杂的计算机系统，均依赖二进制逻辑来进行数据处理和存储。此外，在信息传输和数据编码等领域，二进制也是确保数据准确性的关键。
2.2 二进制数制与其他数制的转换
2.2.1 二进制与十进制的转换方法
二进制转换到十进制的过程是将每一个二进制位按其权值转换为十进制，然后将所有的十进制值相加。具体步骤包括：从二进制数的最低位（最右边）开始，将每一位的数字乘以2的幂次方，幂次从0开始依次增加。然后将这些乘积相加，得到的和就是该二进制数对应的十进制数。
例如，二进制数1101转换为十进制：
1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 8 + 4 + 0 + 1 = 13登录后复制
因此，二进制数1101转换为十进制就是13。
2.2.2 二进制与十六进制的转换方法
二进制转换到十六进制的过程涉及将二进制数分组，每四位一组（从右向左），然后将每组转换成对应的十六进制数。十六进制数制使用16个不同的符号（0-9和A-F）来表示数值。在二进制与十六进制的转换中，每四位二进制数可以直接映射到一个十六进制数。
例如，二进制数10110111转换为十六进制：
二进制分组：10 1101 1111十六进制表示：2 D F登录后复制
因此，二进制数10110111转换为十六进制就是2DF。
2.3 二进制运算规则与应用实例
2.3.1 基本的二进制运算规则
二进制运算规则与十进制类似，主要包括加法、减法、乘法和除法。二进制加法规则为：0+0=0，0+1=1，1+0=1，1+1=10（进位），减法规则为：0-0=0，1-0=1，1-1=0，0-1需要向高位借位，乘法规则为与十进制类似，只是使用2作为基数，除法规则为将二进制数分成若干位进行计算。
2.3.2 二进制运算在计算机中的应用实例
在计算机中，二进制运算是计算机运算的基础，无论是什么样的高级操作最终都会被分解为一系列的二进制运算。例如，在进行图像处理时，图像的每个像素点通常由一组二进制数表示，通过特定的二进制运算可以实现像素颜色的调整，滤镜效果的实现等。在编程语言中，二进制运算也被广泛应用于位运算中，对数据进行高效处理。
下面是一个简单的二进制加法实例，展示了两个二进制数101（5）和110（6）的加法过程：
101+ 1101011登录后复制
将上述二进制数转换为十进制，得到结果5 + 6 = 11。
通过以上章节的介绍，我们可以看到二进制作为计算机科学的基础，它的原理和应用的重要性不言而喻。在接下来的章节中，我们将继续深入探讨二进制数制及其在数据编码、错误检测与校正、数据压缩等高级应用中的作用。
# 3. 数据表示与编码技术## 3.1 数据表示的基本概念### 3.1.1 字符、数字和指令的数据表示在计算机系统中，所有的信息最终都被表示为二进制形式。无论是文本信息、数值还是程序指令，它们都被编码为0和1的序列。字符数据表示涉及文本信息的编码，数字数据表示涉及数值信息的编码，而指令数据表示则涉及程序指令的编码。这一节我们将深入探讨这些数据表示的基本概念和它们如何在计算机中被处理。字符的编码，最典型的是ASCII码，它将每个英文字符与一个7位的二进制数相对应。例如，字符'A'在ASCII码中的值为65，用二进制表示就是1000001。随着计算机系统扩展到了支持多语言，出现了Unicode编码，它用统一的方式为世界上大多数语言中的字符提供了编码。数字数据表示通常涉及整数和浮点数的表示。整数可以通过二进制、八进制或十六进制等不同进制来表示，但计算机内部存储时通常使用二进制形式。浮点数的表示复杂得多，因为它需要编码数值的大小和精度，这在IEEE 754标准中得到规范。指令数据表示则关注于如何将操作码和操作数编码到机器语言中。机器语言是计算机处理器直接理解和执行的低级语言，每条指令都由操作码（指令类型）和可能的操作数（数据位置或具体数值）构成。### 3.1.2 数据宽度对计算机性能的影响数据宽度是指计算机处理数据的位数，常见的是8位、16位、32位和64位。数据宽度直接影响计算机处理数据的效率和速度。一般来说，数据宽度越大，每次能处理的数据量就越多，能够访问的内存空间也越大。以32位和64位为例，一个32位的处理器每次最多可以处理32位的数据，这意味着其一次操作只能处理最多4个字节的数据。一个64位处理器则可以处理8个字节的数据，因此它在处理大数据量或者进行大量计算时会有更高的性能。然而，增加数据宽度也意味着硬件的成本上升，因为寄存器、数据总线、地址总线等都需要扩展以支持更多的位数。数据宽度还会对计算机体系结构产生深远的影响。例如，在32位系统中，处理器能够寻址的内存空间是有限的，通常是4GB。但在64位系统中，可以寻址的内存空间理论上可以达到16EB（Exabyte），即16000000TB，这为大数据和复杂计算提供了广阔的空间。数据宽度同样影响到缓存的效率，以及浮点数运算的性能等。例如，在处理图形和视频时，由于它们需要处理大量的数据，64位架构可以提供更好的性能和更宽的带宽。在执行科学计算和复杂的数学运算时，64位架构可以提供更高的精度和更宽的动态范围。登录后复制