单片机微课程序设计中的PID控制：理论、算法与实战，实现精准控制

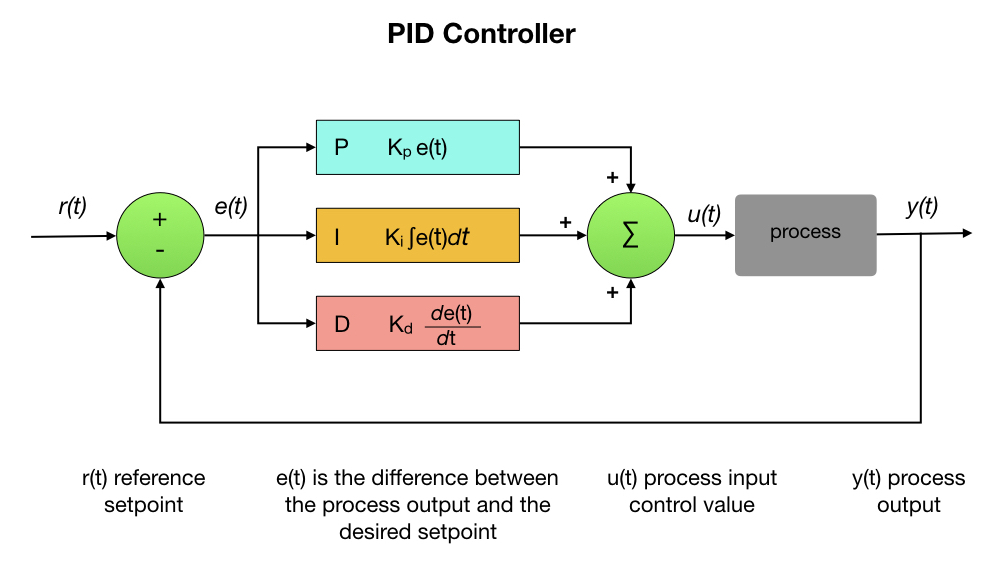
# 1. PID控制的基本原理

PID控制是一种闭环控制系统，它利用反馈机制来实现对被控对象的精确控制。PID控制器通过测量被控对象的输出，并将其与期望的输出进行比较，计算出控制偏差，然后根据偏差的大小和变化率，调整控制输出，以达到期望的控制效果。

PID控制器由三个基本部分组成：比例控制（P控制）、积分控制（I控制）和微分控制（D控制）。P控制根据偏差的大小进行控制，I控制根据偏差的积分进行控制，D控制根据偏差的变化率进行控制。这三个部分共同作用，形成一个综合的控制系统，能够有效地消除控制偏差，实现精确的控制。

# 2. PID控制算法

### 2.1 比例控制（P控制）

**原理：**
比例控制是一种最简单的PID控制算法，其控制输出与误差成正比。误差越大，控制输出越大。

**公式：**

u(t) = Kp * e(t)

其中：

* `u(t)` 为控制输出
* `Kp` 为比例增益
* `e(t)` 为误差，即期望值与实际值的差值

**优点：**
* 简单易于实现
* 响应迅速

**缺点：**
* 存在稳态误差，即当误差为零时，控制输出不为零
* 容易产生振荡

### 2.2 积分控制（I控制）

**原理：**
积分控制通过累加误差来消除稳态误差。随着误差的累积，控制输出逐渐增加，直至误差为零。

**公式：**

u(t) = Kp * e(t) + Ki * ∫e(t)dt

其中：

* `Ki` 为积分增益

**优点：**
* 消除稳态误差
* 提高控制精度

**缺点：**
* 响应较慢
* 容易产生积分饱和，导致控制输出过大

### 2.3 微分控制（D控制）

**原理：**
微分控制通过检测误差的变化率来预测误差的趋势。当误差变化较快时，控制输出会增加，以抑制误差的增长。

**公式：**

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* `Kd` 为微分增益

**优点：**
* 提高控制稳定性
* 抑制振荡

**缺点：**
* 对噪声敏感
* 容易产生微分漂移，导致控制输出不稳定

### 2.4 PID控制器的综合性能

PID控制器综合了比例、积分和微分控制的优点，可以实现良好的控制性能。

**优点：**
* 消除稳态误差
* 提高控制精度
* 抑制振荡
* 提高控制稳定性

**缺点：**
* 需要对三个增益参数进行整定
* 对噪声和干扰敏感

# 3. 单片机微课程序设计中的PID控制**

### 3.1 PID控制器的硬件实现

在单片机微课程序设计中，PID控制器通常通过硬件电路来实现。常用的硬件实现方式有：

- **模拟电路实现：**使用运放、电阻和电容等模拟元件构建PID控制器电路。这种方式简单易行，但精度和稳定性较差。
- **数字电路实现：**使用微控制器或FPGA等数字电路来实现PID控制器算法。这种方式具有精度高、稳定性好、可编程性强等优点。

### 3.2 PID控制算法的软件实现

在单片机微课程序设计中，PID控制算法可以通过软件来实现。常用的软件实现方式有：

- **直接离散化法：**将连续的PID控制算法直接离散化成差分方程，然后在单片机中实现。这种方式简单易行，但精度和稳定性较差。
- **积分法：**使用积分法将连续的PID控制算法离散化成积分方程，然后在单片机中实现。这种方式精度和稳定性较好，但计算量较大。
- **梯形积分法：**使用梯形积分法将连续的PID控制算法离散化成梯形积分方程，然后在单片机中实现。这种方式精度和稳定性介于直接离散化法和积分法之间，计算量也介于两者之间。

**代码块 3.1：梯形积分法实现PID控制算法**

#include <stdint.h>

// PID控制参数
float Kp = 1.0;
float Ki = 0.1;
float Kd = 0.01;

// 误差积分
float integral = 0.0;

// 上一次的误差
float last_