汽车工程中的频率响应分析：提升驾驶体验

# 1. 汽车振动与频率响应**

汽车在行驶过程中会受到各种振动源的影响，如发动机、轮胎和路面不平整等。这些振动会对车辆的舒适性、安全性以及可靠性产生负面影响。

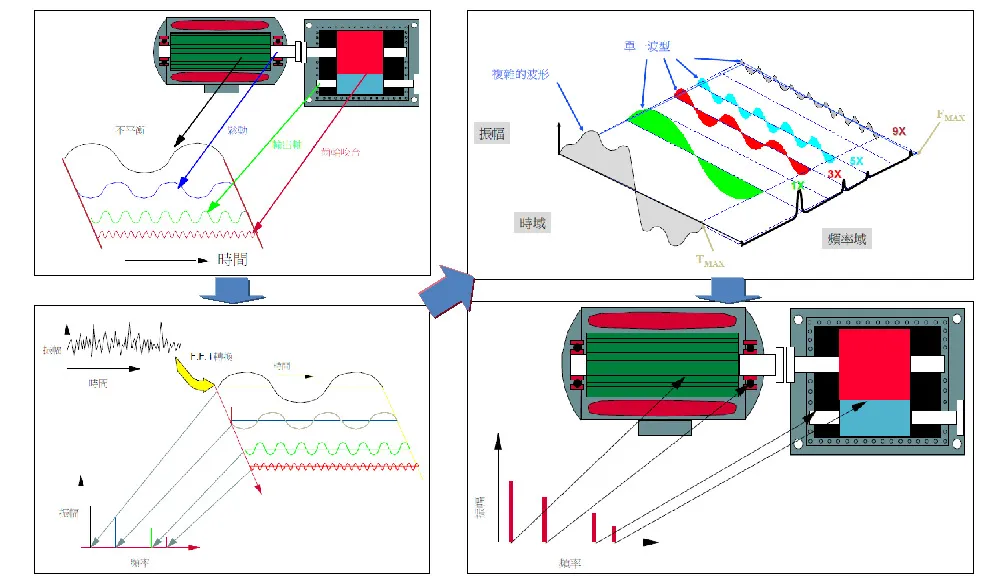
频率响应分析是一种强大的工具，可以帮助工程师了解汽车对不同频率振动的响应。通过分析频率响应，工程师可以识别共振频率，即汽车振动幅度最大的频率。共振频率的存在会放大振动，导致不适、噪音和甚至结构损坏。

频率响应分析对于汽车工程至关重要，因为它可以帮助工程师优化车辆设计，以最大程度地减少振动并提高整体驾驶体验。

# 2. 频率响应分析的理论基础

### 2.1 振动系统的数学模型

#### 2.1.1 单自由度系统

单自由度系统是最简单的振动系统，由一个质量、一个弹簧和一个阻尼器组成。其数学模型为：

m * x''(t) + c * x'(t) + k * x(t) = F(t)

其中：

- `m` 为质量
- `c` 为阻尼系数
- `k` 为弹簧刚度
- `x(t)` 为位移
- `F(t)` 为外力

#### 2.1.2 多自由度系统

多自由度系统由多个质量、弹簧和阻尼器组成，其数学模型更为复杂。一般采用矩阵形式表示：

[M] * {x}''(t) + [C] * {x}'(t) + [K] * {x}(t) = {F}(t)

其中：

- `[M]` 为质量矩阵
- `[C]` 为阻尼矩阵
- `[K]` 为刚度矩阵
- `{x}(t)` 为位移向量
- `{F}(t)` 为外力向量

### 2.2 频率响应函数的计算

#### 2.2.1 频域分析

频域分析将时域信号转换为频域信号，通过傅里叶变换实现。频率响应函数（FRF）定义为系统输出和输入的幅值比：

H(f) = X(f) / F(f)

其中：

- `H(f)` 为频率响应函数
- `X(f)` 为输出信号的傅里叶变换
- `F(f)` 为输入信号的傅里叶变换

#### 2.2.2 时域分析

时域分析直接在时域中计算频率响应函数。通过施加正弦激励，测量系统输出，并使用最小二乘法拟合正弦函数，得到频率响应函数。

H(f) = A / (sqrt((1 - (f / fn)^2)^2 + (2 * zeta * f / fn)^2))

其中：

- `A` 为振幅
- `fn` 为自然频率
- `zeta` 为阻尼比

# 3.1 车辆悬架系统的频率响应分析

**3.1.1 悬架系统的建模和仿真**

车辆悬架系统是一个复杂的多自由度振动系统，其建模和仿真对于频率响应分析至关重要。常用的建模方法包括：

- **刚体-弹簧-阻尼模型：**将悬架系统简化为一系列刚体、弹簧和阻尼器，忽