Mathematica编程挑战：高斯展开法求解薛定谔方程（专家级挑战）

目录
摘要
关键字
1. 量子力学与薛定谔方程

1.1 量子力学基本原理
1.2 薛定谔方程的提出与意义

2. 高斯展开法基础

2.1 高斯函数的数学特性

2.1.1 高斯函数的定义及其积分性质
2.1.2 高斯函数与正态分布的关系

2.2 高斯展开法的理论基础

2.2.1 波函数的高斯展开原理
2.2.2 薛定谔方程的离散化处理

2.3 高斯展开法的数值计算技巧

2.3.1 精确度与效率的平衡

解锁专栏，查看完整目录
摘要
本文系统地介绍了量子力学中薛定谔方程的基本概念及其与高斯展开法的关系，探讨了高斯函数的数学特性，并阐述了高斯展开法的理论基础和数值计算技巧。接着，本文转向Mathematica编程基础，包括其编程范式、基本操作、符号计算和数值分析等，以及如何应用Mathematica实现高斯展开法，并通过实例验证其在求解一维和多维薛定谔方程中的有效性。最后，本文分析了高斯展开法的局限性、改进方向以及在统计物理和量子化学反应动力学等领域的潜在应用，旨在为处理现实物理问题提供数学模型的创新方法和工具。
关键字
量子力学；薛定谔方程；高斯展开法；Mathematica编程；数值计算；物理建模
参考资源链接：高斯展开法求解薛定谔方程的Mathematica实现与算法探讨
1. 量子力学与薛定谔方程
量子力学是现代物理学的基石之一，而薛定谔方程是描述量子系统动态行为的核心。本章将从基础物理概念入手，探讨量子力学的基本原理，并引出薛定谔方程的重要性和基本形式。我们将讨论波函数的物理含义、薛定谔方程的统计解释及其与经典物理的关系。此外，本章还将简要介绍量子力学中的观测问题以及如何将数学表述转化为物理预言。这些内容将为读者提供一个扎实的基础，以便深入理解后续章节中所介绍的高斯展开法以及如何在Mathematica中实现这一算法。
1.1 量子力学基本原理
量子力学的基本原理与经典力学有显著不同。我们将从普朗克的量子假说开始，简述微观粒子的能量量子化现象，并通过德布罗意物质波的概念，引入波粒二象性这一关键概念。波函数作为描述量子态的数学工具，不仅提供了粒子状态的完整信息，还遵循薛定谔方程这一演化规律。本节将解释波函数的概率解释及其对测量结果的预测能力。
1.2 薛定谔方程的提出与意义
薛定谔方程不仅是量子力学的中心方程，也是量子理论的基础。本节将介绍薛定谔方程的物理意义、数学形式，以及它是如何从经典物理中的哈密顿力学演变而来。我们还将探讨薛定谔方程的非相对论性和非定域性特征，以及在不同势能条件下薛定谔方程的具体形式。这一基础的建立为后续章节中高斯展开法的介绍奠定了理论背景。
2. 高斯展开法基础
2.1 高斯函数的数学特性
2.1.1 高斯函数的定义及其积分性质
高斯函数是数学中一种非常重要的函数，特别是在概率论和统计学中，它以均值为μ，标准差为σ的正态分布的概率密度函数而闻名。数学上，一维高斯函数可以表示为：
G(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}登录后复制
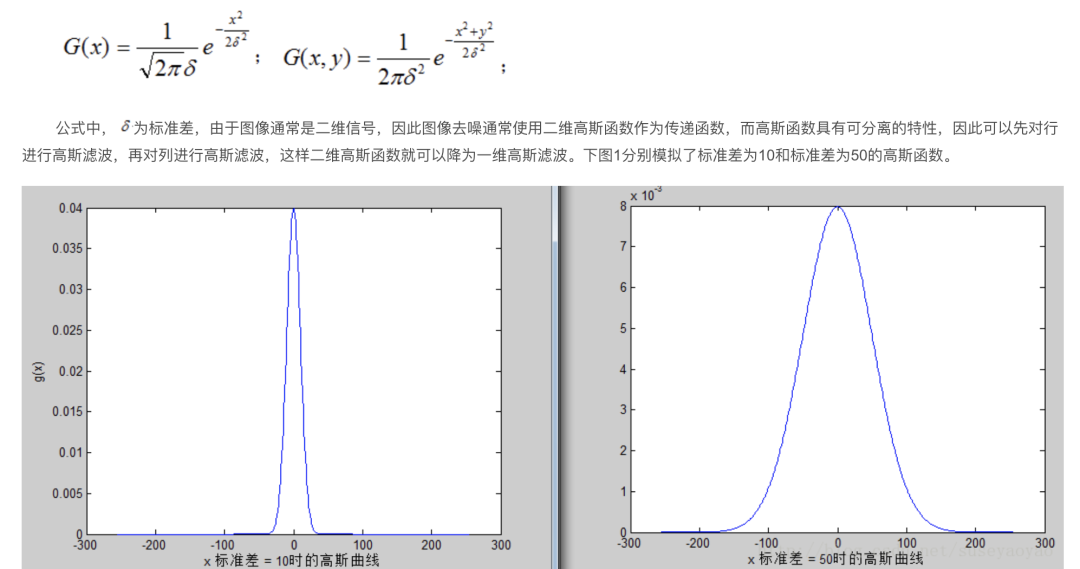
其中，e 是自然对数的底数，π 是圆周率。高斯函数的形状以对称的钟形曲线出现，中心点为均值μ，标准差σ决定了曲线的宽度，σ越小，曲线越窄且尖锐。
在积分性质上，高斯函数具有以下特点：

归一化性质：高斯函数在实数域上的积分为1，确保了它作为概率密度函数的属性。
对称性：关于均值μ对称，即G(μ+x) = G(μ-x)。
不变性：乘以一个常数c，高斯函数的形状不变，只是宽度变化。

高斯函数的这些性质，使得它在求解物理问题时具有独特的数值稳定性和计算效率。
2.1.2 高斯函数与正态分布的关系
高斯函数和正态分布之间的关系是紧密相连的。在统计学中，正态分布（也称为高斯分布）是一种描述自然现象中随机变量分布的模型。正态分布的概率密度函数就是高斯函数。
正态分布的特点包括：

以均值为中心，呈对称分布。
分布的形状完全由均值（μ）和标准差（σ）决定。
两头的尾部无限接近于x轴，但不会与x轴相交，即不会取绝对的零值。

在许多自然和社会现象中，如人的身高、血压、考试成绩等，都近似地符合正态分布。高斯函数因此成为分析这类数据的有力工具。
2.2 高斯展开法的理论基础
2.2.1 波函数的高斯展开原理
在量子力学中，波函数是用来描述微观粒子状态的函数。高斯展开法是一种利用高斯函数的线性组合来近似波函数的方法。通过这种方法，可以将复杂的波函数表达为简单形式的线性叠加，简化计算过程。
高斯展开的核心在于选取适当的高斯函数集合，使得它们的叠加可以逼近任意给定的波函数。高斯函数因其良好的数学性质和物理意义，非常适合作为展开基。
数学上，波函数的高斯展开可以表达为：
\Psi(x) \approx \sum_{i=1}^{N} c_i \cdot G_i(x)登录后复制
其中，c_i 是系数，G_i(x) 是高斯函数。
2.2.2 薛定谔方程的离散化处理
薛定谔方程是量子力学中最基本的方程之一，描述了微观粒子的波函数随时间演化的行为。在实际计算中，为了解决薛定谔方程，经常需要将其离散化处理，从而转换成可以数值求解的形式。
高斯展开法可以在离散化过程中发挥重要作用：

通过选取适当数量和分布的高斯函数，可以构建一个离散的基组来近似波函数。
将离散化的波函数代入离散形式的薛定谔方程，得到一组代数方程。
进一步求解这组代数方程，就可以得到波函数的近似解。

2.3 高斯展开法的数值计算技巧
2.3.1 精确度与效率的平衡
在使用高斯展开法进行数值计算时，一个重要的问题是如何在计算的精确度和效率之间取得平衡。增加高斯函数的数量和优化它们的参数可以提高计算的精确度，但这同时也会增加计算量，降低计算的效率。
为了平衡精确度和效率，可以采取以下策略：

选择合适的高斯函数数量：过多的高斯函数会提高计算复杂度，而太少则可能导致计算结果不够精确。因此，需要根据实际问题的精度要求和计算资源，选择最优的高斯函数数量。
优化高斯参数：高斯函数的参数（如均值和标准差）需要仔细选择，以