计算机基础必知：常见的数据结构及其应用场景

# 1. 数据结构基础概述

### 1.1 什么是数据结构

数据结构是指数据元素之间的关系，以及对这些关系所施加的约束。它是计算机存储、组织数据的方式，能够有效地处理和管理数据。数据结构可以分为线性数据结构和非线性数据结构，是计算机科学的基础知识之一。

### 1.2 数据结构的分类

数据结构根据数据元素之间的关系可以分为线性数据结构和非线性数据结构两大类。线性数据结构中的数据元素之间存在一对一的关系，而非线性数据结构中的数据元素之间存在一对多或多对多的关系。深入理解数据结构的分类有助于我们选择合适的数据结构来解决问题，提高程序的效率和性能。

# 2. 线性数据结构

### 2.1 数组

数组是一种线性数据结构，它由一系列**相同类型的元素**组成，这些元素通过**索引**来标识。数组拥有一些独特的特点，比如：
- **随机访问性**：可以通过索引快速访问数组中的任意元素。
- **连续的内存空间**：数组中的元素在内存中是连续存储的。
- **固定大小**：创建数组时需要指定其大小，且大小通常不可变。

对于不同的应用场景，数组展现出了其独特的优势。比如，在实现**缓存机制**时，可以利用数组的随机访问性来快速获取缓存数据；在**矩阵运算**中，多维数组可以方便表示矩阵。

#### 2.1.1 数组的时间复杂度分析

在数组操作中，不同操作的时间复杂度需要被细致分析：
- **随机访问**：由于数组支持常数时间内的元素访问，其时间复杂度为 O(1)。
- **插入/删除操作**：在数组中插入或删除元素时，需要将后续元素整体向后或向前移动，导致时间复杂度为 O(n)。

通过上述分析可知，在需要频繁进行元素访问操作的场景下，数组的效率较高。

### 2.2 链表

链表是另一种常见的线性数据结构，与数组不同的是，链表中的元素是**通过指针相互连接**起来的。链表包括多种类型，如单链表、双链表和循环链表。

#### 2.2.1 单链表

单链表中的每个节点包含两部分：**数据域**和**指针域**。指针域指向下一个节点，最后一个节点的指针域为 NULL。单链表具有如下特点：
- **插入/删除操作效率高**：在链表中进行插入或删除操作时，只需修改指针指向，时间复杂度为 O(1)。
- **无法随机访问**：无法像数组那样通过索引直接访问元素，需要从头节点开始一个个往下找。

#### 2.2.2 双链表

双链表中每个节点包含两个指针域，分别指向前一个节点和后一个节点。相比单链表，双链表在删除操作时可以更高效地找到前驱节点，从而提高操作效率。

#### 2.2.3 循环链表

循环链表是一种特殊的链表，表尾节点指向表头节点，形成一个环状结构。循环链表常用于需要循环访问的场景，比如实现**循环队列**。

总结来看，数组适合随机访问，而链表适合频繁插入/删除元素的场景。链表的不同类型在不同的应用中展现出各自的特点和优势。

# 3. 非线性数据结构

### 3.1 树

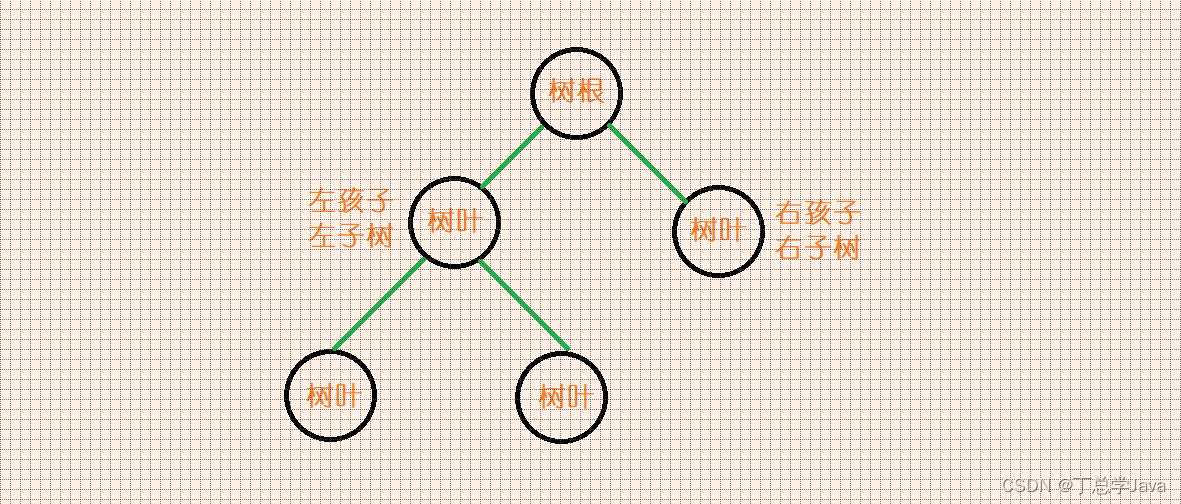
树（Tree）是一种非线性数据结构，由若干个节点组成，节点之间呈现一对多的关系。树结构中包含了根节点、子节点，以及这些节点之间的层级关系。其中，根节点位于树结构的最顶端，子节点则分布在根节点下方，可以有多个子节点，但每个子节点只有一个父节点。

#### 3.1.1 二叉树

二叉树是树结构的一种特殊形式，每个节点最多只有两个子节点，分别为左子节点和右子节点。二叉树可以是空树，也可以是具有以下特性的非空树：

- 每个节点最多有两个子节点；
- 左子节点的值小于父节点，右子节点的值大于父节点；

##### 3.1.1.1 二叉查找树

二叉查找树（Binary Search Tree，简称 BST）是一种特殊的二叉树，具有以下性质：
- 对于树中的每个节点，其左子树的所有节点值都小于该节点的值；
- 对于树中的每个节点，其右子树的所有节点值都大于该节点的值；

通过这种结构，可以实现高效的查找、插入和删除操作，使得查找的时间复杂度保持在 O(log n) 的水平。

##### 3.1.1.2 平衡二叉树

平衡二叉树（Balanced Binary Tree）是一种特殊的二叉树，在其中任何节点的两棵子树的高度差不会超过 1。通过保持树的平衡，可以避免出现极端情况下二叉树退化成链