SVPWM电机控制算法调优


# 摘要
本文对空间矢量脉宽调制（SVPWM）电机控制算法的基础知识、理论模型、实践应用、性能优化以及未来发展趋势进行了深入探讨。首先，介绍了SVPWM算法的基本原理和数学模型，接着阐述了其在电机控制系统中的实现步骤、性能测试和优化策略。然后，分析了提高SVPWM控制系统精度、稳定性和可靠性的方法，以及故障诊断与处理技术。最后，展望了SVPWM算法的智能化方向、新兴领域的应用前景及当前研究的挑战，旨在为电机控制领域提供新的视角和深入理解。

# 关键字
SVPWM算法；电机控制；数学模型；性能优化；系统稳定性；智能化趋势

参考资源链接：[SVPWM原理详解：推导、算法与常见误区矫正](https://wenku.csdn.net/doc/3h7r9yprao?spm=1055.2635.3001.10343)
# 1. SVPWM电机控制算法基础

现代电机控制技术正以日新月异的速度发展，其中，SVPWM（Space Vector Pulse Width Modulation，空间矢量脉宽调制）电机控制算法是一种广泛应用的先进技术。该算法通过空间电压矢量的合成，有效提高了电机控制的性能和效率。在介绍SVPWM电机控制算法的实践应用与优化前，我们需要掌握其基础理论，为深入理解后续章节奠定基础。本章将围绕SVPWM的基本概念、工作原理及其在电机控制领域的基础应用展开介绍。我们将从算法的起源讲起，逐步介绍其基本原理，以及如何将SVPWM技术应用于提升电机驱动系统性能的问题。通过本章的学习，读者应能够理解SVPWM算法的重要性和基础应用，并为深入分析其在电机控制系统中的实践应用做好准备。

# 2. SVPWM算法理论与数学模型

## 2.1 SVPWM算法的原理解析

### 2.1.1 PWM技术概述

脉宽调制（Pulse Width Modulation，PWM）技术是一种通过改变脉冲宽度（即脉冲持续时间与周期的比值）来控制电平高低的数字信号技术。在电机控制中，PWM技术被广泛应用于逆变器的控制，用于调节电压和频率，从而控制电机的转速和转矩。

PWM信号通常由一系列等周期的脉冲组成，每个脉冲的宽度不同。对于一个周期为T的PWM信号，其占空比（Duty Cycle）是脉冲宽度（t）与周期（T）的比值，即D = t/T。通过调整占空比，可以对电机的输入电压或电流进行调节。

在SVPWM中，PWM技术被用于生成空间电压矢量。与传统的正弦波PWM（SPWM）相比，SVPWM通过优化电压矢量的分布，使得逆变器输出电压的基波成分更加接近于理想的圆形旋转磁场，从而提高电机控制的精度和效率。

### 2.1.2 SVPWM算法的数学基础

SVPWM算法基于电压空间矢量的数学模型。在三相交流电机控制系统中，三相电压可以表示为三维空间中的一个矢量。这种表示方法将三相电压的三个分量转换为一个复平面上的矢量，并考虑了它们的幅值和相位信息。

在一个三相坐标系统（即abc坐标系）中，三相电压可表示为：

V_a = V_m * sin(ωt)
V_b = V_m * sin(ωt - 2π/3)
V_c = V_m * sin(ωt + 2π/3)

其中，`V_m` 是相电压的幅值，`ω` 是角频率，`t` 是时间。

通过Clarke变换，可以将abc坐标系下的三相电压转换为两相静止坐标系（即αβ坐标系）下的电压矢量：

V_alpha = V_a
V_beta  = (V_a + V_b + V_c)/sqrt(3)

进一步通过Park变换，可以将αβ坐标系下的电压矢量转换到两相旋转坐标系（即dq坐标系）：

V_d = V_alpha * cos(θ) + V_beta * sin(θ)
V_q = -V_alpha * sin(θ) + V_beta * cos(θ)

其中，`θ` 是旋转坐标系相对于静止坐标系的角度。

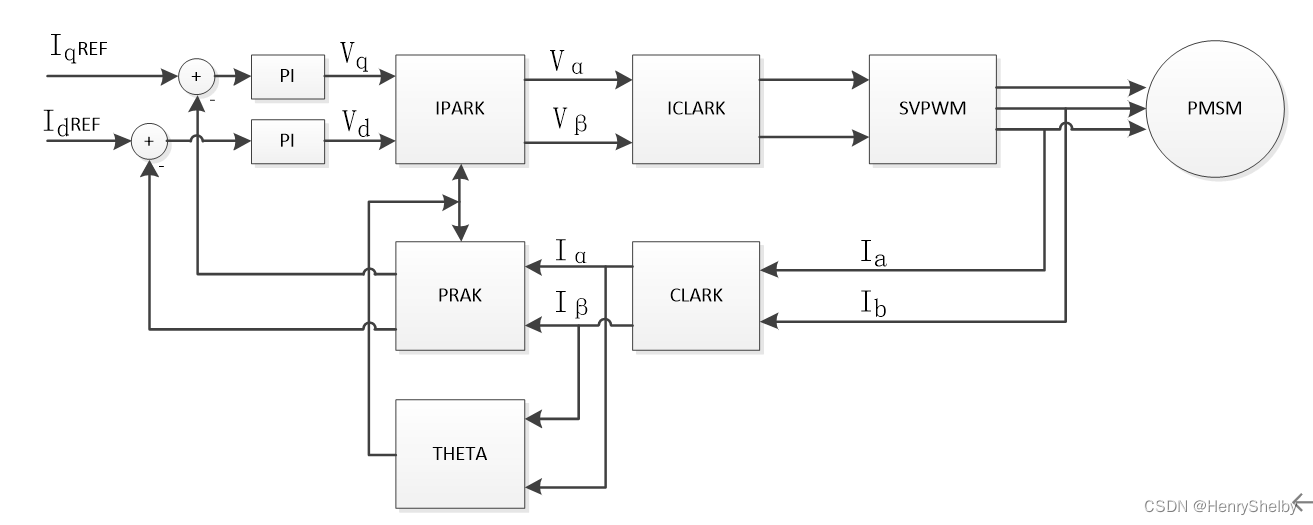
在这个转换过程中，`V_d` 和 `V_q` 分别代表了电压矢量在直接轴（d轴）和交轴（q轴）上的分量，这些分量与电机的磁通量和转矩直接相关。SVPWM算法的核心就是基于这些分量来合成最优的空间电压矢量，以达到高效控制电机的目的。

## 2.2 SVPWM控制模型的建立

### 2.2.1 电压空间矢量的计算方法

为了实现SVPWM控制，首先需要计算出电压空间矢量的大小和方向。电压空间矢量由逆变器六个开关管的状态决定，每个开关管的开或关对应于电压矢量的一个分量。

在一个三相逆变器中，每个桥臂有两个开关管，因此存在8种开关状态。其中，6种有效状态对应于6个非零电压空间矢量（V1到V6），其余2种为零矢量（V0和V7）。这些电压矢量在复平面上呈六边形分布，相邻矢量之间的夹角为60度。

利用开关状态和逆变器输出的直流母线电压，可以计算出每个非零矢量的幅值和相位，如下所示：

V1 = 2/3 * VBus * exp(jπ/6)
V2 = 2/3 * VBus * exp(jπ/2)
V6 = 2/3 * VBus * exp(j5π/6)

其中，`VBus` 是直流母线电压，`exp(jθ)` 表示复数的旋转操作。

### 2.2.2 三相逆变器的控制模型

三相逆变器的控制模型涉及到将直流电源转换为三相交流电的过程。在这个模型中，逆变器的开关管状态变化产生不同的电压矢量，通过合理地控制这些开关状态和相应的占空比，可以生成期望的三相输出电压，从而驱动电机转动。

逆变器的控制策略通常包括：

- 开关频率的选择：开关频率越高，输出电压的谐波越少，但开关损耗增大。
- 开关模式的实现：包括两电平和多电平PWM策略。
- 矢量合成：利用逆变器的开关状态，合成所需的电压矢量。

为了实现这些控制，SVPWM算法通常会采用三个控制周期来实现一个完整的矢量作用时间。具体步骤包括：

1. 计算出参考矢量所在的扇区。
2. 根据扇区分配三个相邻非零矢量的作用时间。
3. 计算零矢量的作用时间。
4. 根据计算出的作用时间，生成PWM信号驱动逆变器。

## 2.3 SVPWM算法的理论优势

### 2.3.1 相对于传统PWM算法的改进

SVPWM算法相对于传统的正弦波PWM（SPWM）算法有诸多改进。SPWM算法主要基于正弦波调制，通过调整正弦波的幅值和频率来控制电机。然而，SPWM在空间矢量利用率上不如SVPWM高效，其输出的电压波形含有较多的谐波成分，导致电机运行效率和性能受限。

SVPWM在输出电压的谐波控制方面具有明显的优势。它优化了电压矢量的分布，使得逆变器产生的电压波形更接近正弦波，减少了谐波的产生。此外，SVPWM算法通过提高空间电压矢量的利用率，使得逆变器的直流母线电压利用率更高，从而在相同直流母线电压条件下获得更大的输出电压幅值。

### 2.3.2 能量效率和动态响应分析

SVPWM算法在能量效率和动态响应方面也有显著的优势。由于SVPWM算法可以更好地利用电压空间，因此它在电机控制系统中可以获得更高的能效比。换句话说，使用SVPWM算法的电机在相同输入功率下可以获得更大的输出功率。

动态响应方面，SVPWM算法能够提供更快速的转矩响应。这是因为它能够更精细地控制电压矢量，实现快速准确的转矩调节。在电机加速或减速过程中，SVPWM算法能够更快地响应控制器的指令，从而减少动态过程中的能量损失和提高整个系统的动态性能。

综上所述，SVPWM算法无论在静态性能（如能量效率）还是在动态性能（如响应速度）方面，都展现出比传统PWM算法更为优越的特性。这些优势使得SVPWM成为了现代电机控制领域的关键技术之一。

# 3. SVPWM算法的实践应用与优化

## 3.1 SVPWM算法的实现步骤

### 3.1.1 空间矢量的合成与分解
空间矢量脉宽调制（SVPWM）是一种先进的电机控制技术，它通过控制逆变器的开关状态来合成所需的电压矢量，进而控制电机的运行。实现SVPWM算法首先需要理解空间矢量的合成与