揭秘虚数单位i：从定义到几何意义的全面解析

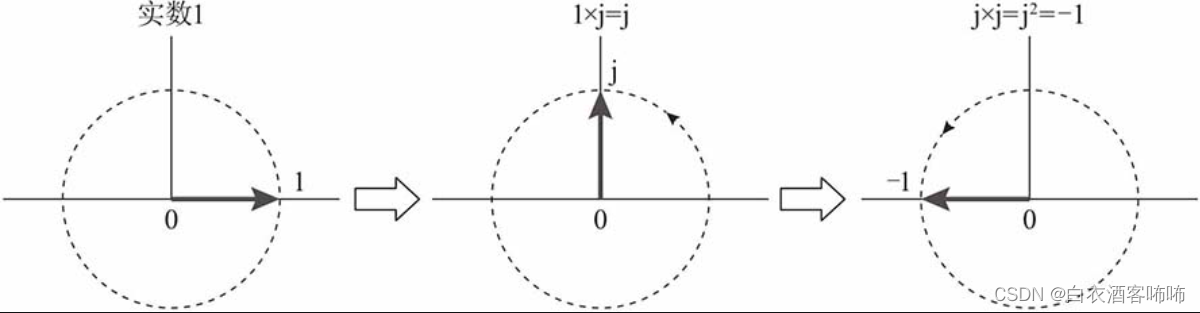
# 1. 虚数单位 i 的定义与性质

虚数单位 i 是一个数学概念，定义为平方等于 -1 的数，即 i² = -1。它在数学、物理和工程等领域中有着广泛的应用。

虚数单位 i 具有以下性质：

- **与实数的乘法：**虚数单位 i 与实数相乘时，会产生一个虚数。例如，3i 是一个虚数。
- **与虚数的加法：**虚数单位 i 可以与其他虚数相加或相减。例如，2i + 5i = 7i。
- **共轭：**虚数单位 i 的共轭是 -i，即 i* = -i。

# 2. 虚数单位i的几何意义

### 2.1 复数平面上的表示

#### 2.1.1 复数的代数形式和几何形式

复数可以表示为代数形式a + bi，其中a和b是实数，i是虚数单位。在几何上，复数可以表示为复数平面上的一个点，其中实数部分a表示点在x轴上的坐标，虚数部分b表示点在y轴上的坐标。

例如，复数3 + 4i在复数平面上表示为点(3, 4)。

#### 2.1.2 复数的模和辐角

复数的模，也称为绝对值，表示复数到原点的距离。模的计算公式为：

|z| = sqrt(a^2 + b^2)

其中z = a + bi是复数。

复数的辐角，也称为参数，表示复数与正实轴之间的夹角。辐角的计算公式为：

arg(z) = arctan(b/a)

其中z = a + bi是复数。

### 2.2 虚数单位i在几何变换中的作用

#### 2.2.1 复数的旋转和缩放

虚数单位i在几何变换中扮演着重要的角色。例如，复数乘以i相当于逆时针旋转90度。复数乘以实数相当于缩放。

以下代码展示了复数旋转和缩放的几何意义：

import cmath

# 定义复数z
z = 3 + 4i

# 旋转90度
z_rotated = z * 1j

# 缩放2倍
z_scaled = z * 2

# 打印旋转和缩放后的复数
print("旋转后的复数：", z_rotated)
print("缩放后的复数：", z_scaled)

输出：

旋转后的复数： (4-3j)
缩放后的复数： (6+8j)

#### 2.2.2 复数的共轭与逆

复数的共轭是将复数的虚部取相反数，即z = a + bi的共轭为z* = a - bi。复数的逆是将复数的模取倒数，并将辐角取相反数，即z = a + bi的逆为z^-1 = (a - bi) / (a^2 + b^2)。

共轭和逆在几何变换中也有重要的意义。共轭相当于在复数平面上关于x轴对称，而逆相当于在原点关于单位圆对称。

以下代码展示了复数共轭和逆的几何意义：

import cmath

# 定义复数z
z = 3 + 4i

# 共轭
z_conjugate = z.conjugate()

# 逆
z_inverse = 1 / z

# 打印共轭和逆
print("共轭：", z_conjugate)
print("逆：", z_inverse)

输出：

共轭： (3-4j)
逆： (0.12-0.16j)

# 3. 虚数单位i在数学中的应用

### 3.1 代数方程的求解

虚数单位i在代数方程的求解中发挥着至关重要的作用。

#### 3.1.1 一次方程和二次方程

对于一次方程ax+b=0，其中a和b为实数，如果a≠0，则方程的解为x=-b/a。然而，如果a=0，则方程要么无解（当b≠0时），要么有无穷多个解（当b=0时）。

当涉及到二次方程ax²+bx+c=0时，虚数单位i就派上用场了。二次方程的判别式Δ=b²-4ac决定了方程的解的性质。

- 如果Δ>0，则方程有两个不同的实根：x₁=(-b+√Δ)/2a和x₂=(-b-√Δ)/2a。
- 如果Δ=0，则方程有两个相等的实根：x₁=x₂=-b/2a。
- 如果Δ<0，则方程有两个共轭复根：x₁=(-b+i√|Δ|)/2a和x₂=(-b-i√|Δ|)/2a。

#### 3.1.2 高次方程的复数根

虚数单位i还用于求解高次方程，例如三次方程和四次方程。虽然高次方程的复数根可能无法用实数根式表示，但虚数单位i允许我们找到这些根的近似值。

### 3.2 微积分中的应用

虚数单位i在微积分中也有着广泛的应用。

#### 3.2.1 复变函数的导数和积分

复变函数是定义在复数域上的函数。虚数单位i允许我们对复变函数求导和积分。

复变函数f(z)的导数定义为：

f'(z) = lim(h->0) [f(z+h) - f(z)]/h

复变函数f(z)的积分定义为：

∫f(z) dz = F(z) + C

其中F(z)是f(z)的一个原函数，C是一个复数常数。

#### 3.2.2 柯西积分定理

柯西积分定理是一个重要的复变分析定理，它指出：如果f(z)是一个在复平面上的开区域内解析的函数，那么沿着该区域内任何闭合路径的积分等于0。

柯西积分定理在求解复变函数的积分以及其他复变分析问题中有着广泛的应用。

# 4. 虚数单位i在物理学中的应用

虚数单位i在物理学中扮演着至关重要的角色，它为电磁学和量子力学等领域提供了强大的数学工具。

### 4.1 电磁学中的复数阻抗

#### 4.1.1 阻抗的概念和复数表示

在电磁学中，阻抗是衡量电路中电流通过困难程度的量。它由电阻、电感和电容三个因素共同决定。对于交流电路，阻抗是一个复数，可以用以下形式表示：

Z = R + jX

其中：

* R 为电阻，单位为欧姆（Ω）
* X 为电抗，单位为欧姆（Ω）
* j 为虚数单位

电抗又可分为感抗（XL）和容抗（XC），分别表示电感和电容对电流的阻碍作用：

XL = 2πfL
XC = 1 / (2πfC)

其中：

* f 为交流电的频率，单位为赫兹（Hz）
* L 为电感，单位为亨利（H）
* C 为电容，单位为法拉（F）

#### 4.1.2 复数阻抗在电路分析中的应用

复数阻抗在电路分析中具有重要意义。它允许工程师使用简单的数学运算来求解复杂的交流电路问题。例如，在串联电路中，总阻抗等于各个阻抗的代数和：

Z_total = Z_1 + Z_2 + ... + Z_n

而在并联电路中，总阻抗等于各个阻抗的倒数和的倒数：

1 / Z_total = 1 / Z_1 + 1 / Z_2 + ... + 1 / Z_n

### 4.2 量子力学中的波函数

#### 4.2.1 波函数的复数形式

在量子力学中，波函数是一个描述粒子状态的复数函数。它包含了粒子的所有可能状态的信息，包括位置、动量和自旋。波函数通常用以下形式表示：

ψ(x, t) = A(x, t)e^(iθ(x, t))

其中：

* A(x, t) 为波函数的幅度，表示粒子在位置x和时间t处出现的概率密度
* θ(x, t) 为波函数的相位，表示粒子的波函数在空间和时间中的振荡

#### 4.2.2 波函数的概率解释

波函数的幅度平方（|ψ(x, t)|^2）表示粒子在位置x和时间t处出现的概率密度。这意味着波函数的幅度越大，粒子出现在该位置的可能性就越大。

波函数的相位与粒子的波函数的振荡有关。它不能直接测量，但它在量子力学中起着至关重要的作用，因为它决定了粒子的干涉和衍射行为。

# 5. 虚数单位i的哲学与文化影响

### 5.1 虚数单位i的发现与数学的革新

#### 5.1.1 虚数单位i的起源

虚数单位i的发现是一个数学史上的重大事件。在16世纪，意大利数学家吉罗拉莫·卡达诺在研究三次方程的求解时，遇到了无法用实数根来解决的情况。为了解决这个问题，卡达诺引入了一个新的概念，即“虚数”。虚数被定义为平方等于-1的数，用符号i表示。

#### 5.1.2 虚数单位i对数学体系的影响

虚数单位i的引入对数学体系产生了深远的影响。它扩展了实数域，使得代数方程有了更多的解。虚数还被用于复分析、拓扑学和量子力学等数学领域中。

### 5.2 虚数单位i在文学与艺术中的隐喻

#### 5.2.1 虚数单位i作为想象与未知的象征

虚数单位i经常被用作想象和未知的象征。在文学中，虚数单位i代表着无法用理性思维理解的事物，例如梦想、幻想和超自然现象。

#### 5.2.2 虚数单位i在超现实主义与现代主义中的应用

在20世纪初的超现实主义和现代主义艺术运动中，虚数单位i被用作一种挑战传统和探索未知的手段。超现实主义画家萨尔瓦多·达利经常在他的作品中使用虚数单位i，以表达潜意识和非理性的世界。