【信号处理艺术】：时域与频域信号增强策略


# 摘要
本文综合回顾了信号处理的基础知识，并详尽地探讨了时域和频域信号增强技术，包括噪声去除、特征提取、信号重构与压缩、滤波与增强等方法。通过分析时频分析技术及其变体，本文深入研究了信号增强的理论局限性与实践挑战，并探讨了信号增强技术在现代信号处理中的多种应用。文章还展望了人工智能、机器学习和新兴技术对信号增强领域的影响和未来研究方向，提出了多种优化方法和策略创新，以应对大数据环境下的信号处理需求。

# 关键字
信号处理；噪声去除；特征提取；时频分析；人工智能；大数据信号处理

参考资源链接：[MATLAB实现时域频域特征提取的完整代码解析](https://wenku.csdn.net/doc/46ku81r8g7?spm=1055.2635.3001.10343)
# 1. 信号处理的基础知识回顾

## 1.1 信号的分类与表示
信号处理的领域广泛而深入，其核心在于对信号的理解和分类。信号按其时间特性可分类为时域信号和频域信号。时域信号直接依赖于时间变量，而频域信号则是通过频率成分来表达。数学表示上，连续时间信号通常用函数\( x(t) \)来表示，而离散时间信号则使用序列\( x[n] \)。

## 1.2 基本信号处理概念
信号处理涉及多个基本概念，例如线性时不变系统（LTI），它遵循叠加原理和时间不变性。傅里叶分析是信号处理中的一个重要工具，它能够将时域信号转换到频域进行分析。傅里叶级数用于周期信号，而傅里叶变换则适用于非周期信号。拉普拉斯变换和Z变换在系统分析和信号处理中也有重要地位，它们能够帮助我们理解系统稳定性和信号的频谱特性。

## 1.3 信号处理的重要原则
信号处理过程需遵循一些核心原则，包括信号的采样、量化、以及重建。根据奈奎斯特定理，当采样频率至少为信号最高频率的两倍时，原始信号可以被无失真地重建。量化误差和量化噪声也是信号处理中需考虑的因素，它们影响信号的质量和数据处理的准确性。

在后续章节中，我们将深入探讨信号增强技术，包括时域和频域的方法，以及它们在实际应用中的运用和优化。

# 2. 时域信号增强技术

## 2.1 时域信号的噪声去除

### 2.1.1 基于滤波器的噪声去除方法

在处理时域信号时，噪声去除是提高信号质量的关键步骤。噪声通常是信号中不需要的、非期望的组成部分，它会干扰我们对信号的理解和分析。利用滤波器进行噪声去除是常用的方法之一，因为它能够通过设计特定的频率响应来减少或去除噪声。

滤波器的种类很多，最基本的是低通、高通、带通和带阻滤波器。例如，低通滤波器可以被用来去除高频噪声，因为其设计使低频信号通过而阻止高频信号。在实际应用中，工程师可以根据信号的特性和噪声的频谱来选择或设计合适的滤波器。

设计滤波器时，需要考虑的关键参数包括截止频率、滤波器的阶数、以及滤波器的类型（如巴特沃斯、切比雪夫、椭圆等）。这些参数将决定滤波器的性能，比如过渡带宽度、纹波大小以及群延迟特性等。

### 2.1.2 信号平滑技术

除了滤波器之外，信号平滑技术也是去除噪声的常见方法之一，特别是在处理生物医学信号或金融时间序列数据时。信号平滑技术的目的是减少或消除信号的随机波动，使信号更加平滑。

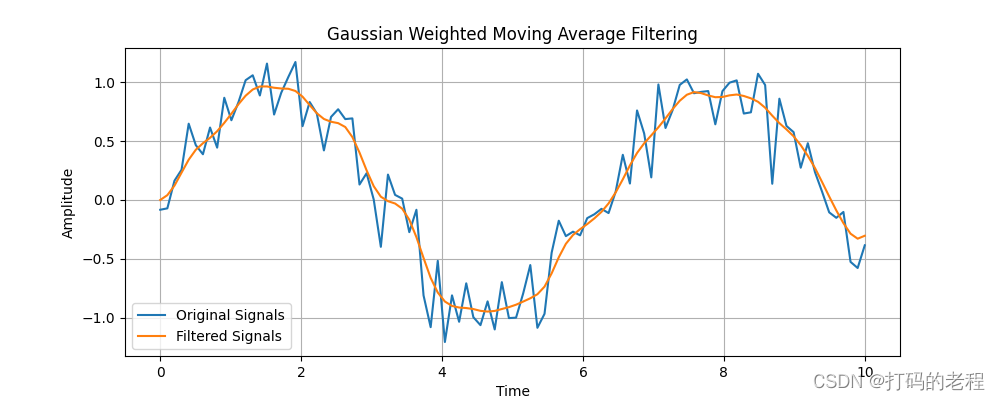
常用的信号平滑技术包括移动平均法和加权移动平均法。移动平均法通过对一定数量的连续样本值进行算术平均来得到当前点的估计值。加权移动平均法在计算平均时给予较近的数据点更高的权重，这通常能够提供更好的平滑效果。

### 2.1.3 信号去噪的自适应方法

自适应滤波器在处理非平稳噪声时表现尤为突出，因为它能够实时地调整自己的参数来适应信号的变化。与固定的滤波器设计不同，自适应滤波器可以在线更新滤波器系数，这使其成为处理实时信号的理想选择。

自适应滤波器的核心是通过最小化误差信号来调整滤波器系数的算法。常见的算法包括最小均方（LMS）算法及其变体，这些算法能够自动适应输入信号的统计特性，从而有效地去除噪声。

自适应方法的一个挑战是需要选择合适的算法和参数，如步长因子、滤波器长度等，以确保算法的收敛性和去噪效果。

## 2.2 时域信号的特征提取

### 2.2.1 时域信号的统计特征分析

特征提取是信号处理中的一个重要环节，它从原始信号中提取出有助于后续分析和分类的关键信息。在时域分析中，统计特征如均值、方差、偏度和峰度常被用来描述信号的特性。

均值可以告诉我们信号的整体水平，方差反映信号的波动程度，而偏度和峰度则描述了信号的分布形态。这些特征经常在模式识别和机器学习任务中被用来作为特征向量的一部分。

### 2.2.2 特征选择与降维技术

在高维数据中，提取出的特征数量可能非常庞大，这会使得后续的处理和分析变得复杂和耗时。因此，进行特征选择和降维是一个重要的步骤。特征选择的目的是识别出对于特定任务最有用的特征子集，而降维技术如主成分分析（PCA）和线性判别分析（LDA）则旨在减少数据的维数，同时尽可能保留原始数据中的信息。

### 2.2.3 实际应用案例分析

在本节中，我们将探讨一个实际的案例，通过分析真实的时域信号来展示特征提取的过程。例如，我们可以考虑人体步态信号的特征提取，这对于步态分析和生物力学研究非常有用。在这个应用中，我们可能需要从步态信号中提取出步态周期、步幅、对称性、稳定性等特征，并使用这些特征来区分不同个体的步态模式。

通过这个案例，我们将展示如何应用前面提到的统计特征分析和特征选择技术来处理原始的时域信号数据，并最终得到有助于分类和理解的特征向量。

## 2.3 时域信号的重构与压缩

### 2.3.1 信号重构方法论

信号重构是指从一系列观测数据中重建出原始信号的过程。在许多应用中，由于设备限制或传输过程中的数据丢失，我们可能只能得到部分信号信息，信号重构技术帮助我们从这些不完整的数据中恢复出尽可能接近原始信号的数据。

信号重构的基础是信号的稀疏表示，即在适当的变换域中，信号可以表示为少量非零系数和大量零系数的组合。常见的变换域包括傅里叶变换、小波变换等。通过找到合适的变换和算法，比如正则化技术或压缩感知，我们可以实现有效的信号重构。

### 2.3.2 压缩感知技术

压缩感知（Compressed Sensing, CS）是一种革命性的信号处理方法，它表明如果一个信号在某个变换域是稀疏的，那么我们可以使用远少于奈奎斯特采样定律要求的采样点数来采集信号，然后通过优化算法重建出原始信号。

压缩感知的核心是信号的稀疏表示和非线性重构算法，常用的重构算法包括基追踪（BP）、匹配追踪（MP）及其变体。这些算法能够在已知信号稀疏变换和观测矩阵的情况下，从远少于信号长度的测量中准确地重构出信号。

### 2.3.3 应用于数据压缩的策略

压缩感知不仅在信号重构方面有所应用，它也被广泛用于数据压缩。在许多应用场景中，如无线传感器网络和医疗影像，信号或数据的传输和存储都需要有效的压缩策略。

为了使用压缩感知进行数据压缩，我们可以设计一个或多个测量矩阵来从原始信号中获得少量的线性测量值。然后，通过合适的重构算法从