冒泡排序：从平凡到卓越的优化之旅

# 1. 冒泡排序算法概述

冒泡排序（Bubble Sort）算法是计算机科学中最简单且常见的排序算法之一。尽管它的效率通常不高，但由于其易于理解和实现，经常作为算法入门的教学案例。在这一章节中，我们将简要介绍冒泡排序的基本概念、它的应用场景以及为何它在实际应用中的效率并不是最优的选择。随后，我们将更深入地探讨冒泡排序的理论基础、实现方法以及优化技巧，以帮助读者更全面地理解和掌握这一基础算法。

# 2. 冒泡排序的理论基础

冒泡排序是一种简单的排序算法，它是通过重复走访要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复进行直到没有再需要交换，也就是说该数列已经排序完成。

## 2.1 算法的基本概念和步骤

### 2.1.1 冒泡排序的定义

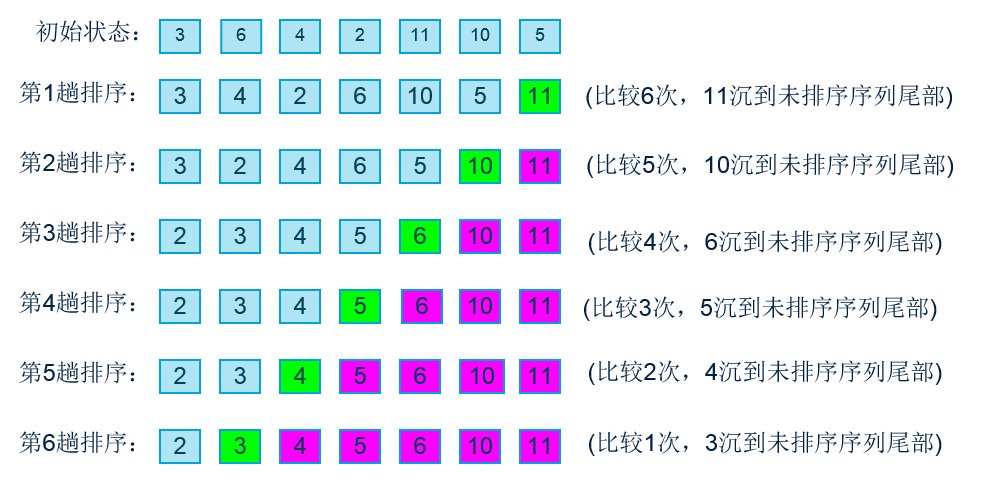
冒泡排序是一种比较型排序算法，其基本思想是通过对待排序序列从前向后（从下标较小的元素开始），依次比较相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前移向后部，就像水底下的气泡一样逐渐向上冒。

### 2.1.2 算法的基本步骤解析

假设我们有一组数据需要进行排序：[5, 1, 4, 2, 8]。

1. 第一趟排序：比较5和1，发现5>1，交换位置，得到序列[1, 5, 4, 2, 8]；然后比较5和4，交换位置，得到[1, 4, 5, 2, 8]；继续比较5和2，交换位置，得到[1, 4, 2, 5, 8]；最后比较5和8，不需要交换。
2. 第二趟排序：此时5已经在正确的位置，我们从头开始，比较1和4，不需要交换；比较4和2，交换位置，得到[1, 4, 2, 5, 8]；比较2和5，不需要交换；最后比较5和8，不需要交换。
3. 第三趟排序：我们发现序列已经是有序的，不再需要任何交换。

## 2.2 算法复杂度分析

### 2.2.1 时间复杂度

冒泡排序的时间复杂度取决于输入数据的初始状态。在最好情况下（输入数据已经是排序好的），时间复杂度为O(n)，因为只需要遍历一次数据就可以确定不需要进一步的交换。在最坏情况下（输入数据是逆序的），每次比较都需要交换，时间复杂度为O(n^2)，因为需要进行n-1趟排序，每趟排序需要进行n-i次比较，i从1到n-1。在平均情况下，时间复杂度也是O(n^2)。

### 2.2.2 空间复杂度

冒泡排序是一种原地排序算法，因此它的空间复杂度为O(1)。这表示它不需要额外的存储空间，只需要一个临时变量来完成交换操作。

### 2.2.3 理论上的最优与最坏情况

冒泡排序的理论最优情况发生在输入数据已经完全有序时，此时算法的效率最高，时间复杂度降至O(n)。理论上最坏的情况发生在输入数据完全逆序时，此时需要进行最大数量的比较和交换操作，时间复杂度为O(n^2)。

在本章节中，我们详细讨论了冒泡排序的理论基础，包括其定义、基本步骤以及时间复杂度和空间复杂度的分析。这为进一步探讨冒泡排序的实现和优化打下了坚实的基础。接下来的章节将深入探讨冒泡排序的具体编码实现及其优化策略，以提高算法的实际应用效率。

# 3. 冒泡排序的实现与优化

## 3.1 基本冒泡排序的编码实现

冒泡排序是一种简单的排序算法，它重复地遍历待排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行直到没有再需要交换，也就是说该数列已经排序完成。这一过程是将最大数“浮”到数列的顶端，就像水中的气泡一样。

### 3.1.1 未优化的冒泡排序代码

以下是未优化的冒泡排序实现的代码示例，这是在Python中的实现：

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

这段代码的逻辑非常直观：
- 第一层循环负责从数组的第一个元素到最后一个元素依次进行比较。
- 第二层循环负责在未排序的部分进行相邻元素的比较和交换。
- 如果当前元素比下一个元素大，则交换它们的位置。

### 3.1.2 排序过程的可视化

为了更清楚地理解冒泡排序的过程，我们可以通过可视化的方法来展示。下面是一个简单的Python脚本，使用了matplotlib库来绘制每一步排序过程的数组状态：

import matplotlib.pyplot as plt
import numpy as np

def visualize_bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        arr = bubble_sort(arr)
        print(f"Step {i+1}: {arr}")
        plt.bar(range(n), arr)
        plt.show()

arr = [64, 34, 25, 12, 22, 11, 90]
visualize_bubble_sort(arr)

此脚本会逐次对数组进行一次完整遍历，并在每次遍历后打印数组的状态，并用条形图的形式展示数组的状态。

## 3.2 冒泡排序的优化技巧

冒泡排序虽然简单，但在实际应用中效率较低，尤其在数据量较大时。因此，为了提高效率，研究者们提出了多种优化冒泡排序的策略。

### 3.2.1 标记优化法

标记优化法的核心思想是引入一个标记，用于判断在一次遍历中是否发生了元素交换。如果没有发生交换，说明数组已经是排序状态，算法可以立即结束。以下是标记优化法的Python实现：

def optimized_bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        swapped = False
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
                swapped = True
        if not swapped:
            break
    return arr

### 3.2.2 鸡尾酒排序变种

鸡尾酒排序是冒泡排序的一个变种，其过程与冒泡排序类似，只不过是从低到高再从高到低进行两次遍历排序。在每轮遍历过程中，它同时考虑向上和向下两个方向的比较和交换。以下是鸡尾酒排序的Python实现：

def cocktail_shaker_sort(arr):
    n = len(arr)
    swapped = True
    start = 0
    end = n - 1

    while swapped:
        swapped = False

        # 从左到右进行冒泡排序
        for i in range(start, end):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]
                swapped = True

        # 如果没有交换发生，说明数组已经排序完成
        if not swapped:
            break
        swapped = False

        # 减小最后一个元素索引，因为最后的元素已经是最大的了
        end -= 1

        # 从右到左进行冒泡排序
        for i in range(end - 1, start - 1, -1):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]
                swapped = True

        # 增加起始元素索引，因为第一轮的起始元素已经是最小的了
        start += 1

    return arr