希尔排序深度解码：分组排序的艺术详解

# 1. 希尔排序的基本概念

## 1.1 排序简介
排序是将一组数据按照特定的顺序（通常是从小到大或从大到小）进行排列的处理过程。在计算机科学中，排序是数据处理的基本操作之一，广泛应用于各类算法和数据结构中。

## 1.2 希尔排序的起源
希尔排序由Donald Shell于1959年提出，是早期为数不多的几种能够适应不同大小数据集的高效算法之一。它的出现，简化了之前复杂且效率低下的排序方法。

## 1.3 排序算法的必要性
在信息时代，大量的数据需要被处理和分析。因此，高效的排序算法不仅可以提升数据处理的速度，还可以降低计算资源的消耗。希尔排序作为一种简单而又高效的算法，其基本概念是后续深入讨论的基础。

# 2. 希尔排序的理论基础

## 2.1 排序算法的分类与发展

### 2.1.1 排序算法的性能指标

排序算法作为计算机科学中的基础，其性能指标主要体现在时间复杂度、空间复杂度、稳定性以及实现复杂度等方面。时间复杂度关注算法执行所需的运算次数，它决定了算法运行的快慢。空间复杂度涉及算法执行过程中占用的存储空间。稳定性则描述了排序前后，相等元素的相对次序是否保持不变。实现复杂度则是评估排序算法编码的难易程度。

在对排序算法进行评估时，通常会关注以下性能指标：

- **时间复杂度**：通常分为最坏情况、平均情况和最好情况。
- **空间复杂度**：描述算法运行所需的额外空间。
- **稳定性**：排序过程中保持相等键值元素的相对顺序。
- **实现复杂度**：算法编码的复杂性和理解难度。

通过这些性能指标，可以全面地评价一个排序算法的适用场景和效率。

### 2.1.2 排序算法的比较和选择

在比较和选择排序算法时，开发者通常根据具体的应用场景来决定。例如，若需要排序大量数据且数据量未知，可能会倾向于选择时间复杂度较低的排序算法，如快速排序。若对稳定性有要求，则可能会选择归并排序。

为了选择最适合的排序算法，以下是一些评价标准：

- **数据规模**：算法对不同规模数据的适应性。
- **数据初始状态**：数据的初始排列对算法效率的影响。
- **运行环境**：算法在不同的硬件和操作系统上的表现。
- **内存使用**：算法对内存资源的需求和利用效率。

开发者在选择排序算法时，不仅要考虑算法本身的性能，还需要结合实际应用环境和需求进行权衡。

## 2.2 希尔排序的原理和特点

### 2.2.1 希尔排序的排序步骤

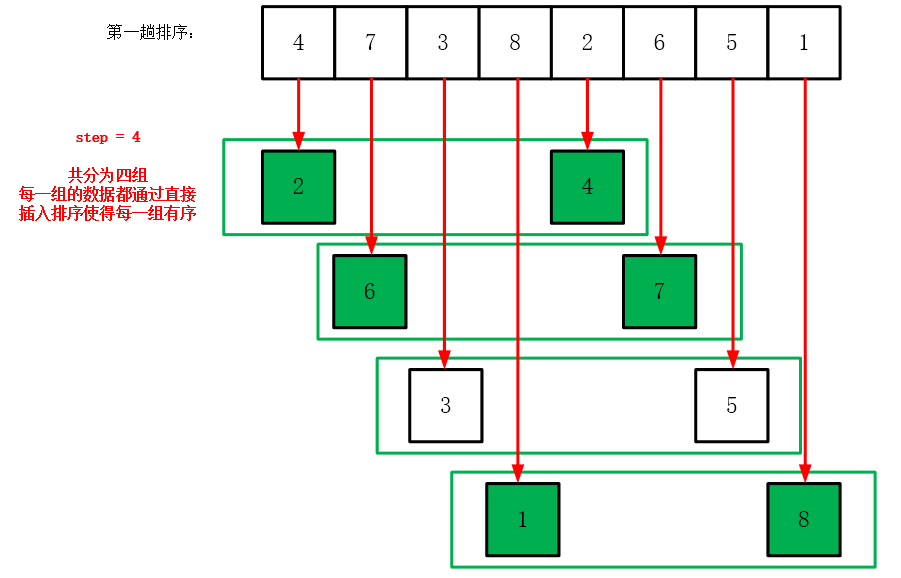
希尔排序是一种插入排序的改进版，它通过引入间隔序列（也称作增量序列）来减少数据移动的次数，从而提高效率。其基本步骤如下：

1. **确定增量序列**：选择一个增量序列`t1, t2, ..., tk`，其中`t1 = 1`。
2. **进行分组**：按照增量序列对数组进行分组，每组内部使用插入排序。
3. **缩小增量**：缩小增量，重复第二步，直到增量为1，此时进行普通插入排序。

希尔排序的优势在于减少了比较和交换的次数，特别是在数据基本有序的情况下，效率尤为显著。

### 2.2.2 希尔排序的优势分析

希尔排序的主要优势在于：

- **效率较高**：相较于普通的插入排序，在中等大小的数据集上表现出色。
- **容易实现**：虽然引入了间隔序列的概念，但算法的核心步骤仍然简单易懂。
- **无需额外空间**：希尔排序是原地排序，不需要额外的存储空间。

然而，希尔排序也有其劣势，比如对间隔序列的选择依赖较大，不恰当的选择可能导致性能下降。

## 2.3 排序算法的稳定性与时间复杂度

### 2.3.1 稳定性在排序中的重要性

排序算法的稳定性是一个重要的属性，特别是在需要排序的数据中包含多个具有相同关键值的记录时。稳定性意味着算法能够保持这些记录的相对顺序不变。

稳定性在以下几个方面具有重要性：

- **排序后的数据处理**：例如，在数据库查询结果中，可能需要根据多个字段进行排序。稳定的排序算法可以保证前一个字段排序的结果在后一个字段排序后仍然有效。
- **数据的有序性维护**：在某些情况下，数据集中的元素已经部分有序，使用稳定的排序算法可以减少排序的工作量。

### 2.3.2 希尔排序的时间复杂度分析

希尔排序的时间复杂度受到间隔序列选择的影响，一般情况下，其最好、平均、最坏情况的时间复杂度分别为`O(n log n)`、`O(n log n)`、`O(n^2)`。但通过合适的间隔序列选择，可以显著提高算法在最坏情况下的表现。

希尔排序的性能主要取决于：

- **间隔序列的选择**：好的间隔序列能够使得算法具有更好的性能。
- **数据的初始状态**：部分有序的数据集可以提高希尔排序的效率。
- **内部插入排序的效率**：由于希尔排序在每一步中都使用插入排序对分组进行排序，因此插入排序的效率也会影响希尔排序的整体性能。

总结而言，虽然希尔排序不是最稳定的排序算法，但通过优化间隔序列的选择，可以在实践中获得较好的性能表现。

# 3. 希尔排序的实现细节

在探讨希尔排序的实现细节之前，首先需要明白一个核心思想：间隔序列的选择和排序步骤是希尔排序中最为关键的部分，它们共同决定了排序的效率。本章节将详细解析间隔序列的选择方法，并通过伪代码和多种编程语言实例展示希尔排序的实现。之后，我们将深入探讨如何优化希尔排序算法以提高其性能。

## 3.1 希尔排序中的间隔序列选择

希尔排序是一种分组排序方法，而间隔序列的选择直接影响着排序算法的性能。我们需要深入分析间隔序列的理论基础，并进行实践测试，以选择最佳的间隔序列。

### 3.1.1 最佳间隔序列的理论和实践

理论上，间隔序列的选择应满足两个条件：首先，序列的起始值要足够大，以使分组后的数组具有较好的分布性；其次，随着排序的进行，间隔值应逐渐减小，直到最后为1，此时整个数组将进行一次类似插入排序的步骤，以保证最终排序的稳定性。

实