电力电子工程师必读：SVPWM工业应用挑战与解决方案


# 摘要
本文全面介绍了SVPWM（Space Vector Pulse Width Modulation，空间矢量脉宽调制）技术，涵盖了其技术概述、理论基础、数学模型、算法实现以及在电力系统中的应用挑战。通过对SVPWM的工作原理、数学模型和算法步骤的详细解析，阐述了其相较于传统PWM技术的优势。同时，文章分析了SVPWM在系统设计和实际运行中遇到的挑战，如死区效应和环境因素的影响，并探讨了工业应用中的优化策略，包括硬件设计、软件控制策略以及预测与故障诊断技术。案例分析部分展示了SVPWM在工业实践中的成功应用与效果评估。最后，本文预测了SVPWM技术未来的发展趋势，包括技术创新、行业标准的制定以及新能源领域的发展潜力。

# 关键字
SVPWM；空间矢量理论；数学模型；算法实现；电力系统；工业应用优化

参考资源链接：[SVPWM技术解析：优化电机控制与谐波减少](https://wenku.csdn.net/doc/6401ad08cce7214c316ee0af?spm=1055.2635.3001.10343)
# 1. SVPWM技术概述

SVPWM（Space Vector Pulse Width Modulation）技术是现代电力电子技术中的一项重要技术，广泛应用于电机驱动、电力转换等领域。作为一种高效的调制策略，SVPWM具有高效率、低损耗、小体积、强适应性等特点，已成为电力系统优化升级的关键技术之一。

本章将从SVPWM技术的基本概念讲起，深入解析其工作原理、数学模型以及在电力系统中的实际应用。通过了解SVPWM的基本知识，我们可以更好地掌握这项技术在电力系统控制中的作用，并探讨如何优化应用以应对未来挑战。

## 1.1 SVPWM技术简介

SVPWM技术的核心在于通过优化PWM（脉冲宽度调制）波形来提高电力转换的效率。利用三相交流电机的相电压空间矢量，SVPWM技术能够在保持电压有效值不变的情况下，降低电机的谐波损耗，提高电流波形的质量。

## 1.2 SVPWM的优越性

相较于传统PWM，SVPWM在实现同等开关频率的同时，能够达到更高的直流电压利用率。这种特性使得SVPWM在高精度、大容量的电机控制应用中表现出色。通过精确控制开关时间，SVPWM技术能够有效减少开关器件的开关次数，降低损耗，提升系统的整体效率。

## 1.3 SVPWM技术的发展与应用

随着电力电子技术的不断进步，SVPWM技术也在不断地完善和发展。从最初的基本算法到现在融入先进的控制策略，SVPWM技术在工业、新能源、轨道交通等多个领域得到了广泛应用，成为提升电力系统性能的重要工具。

在接下来的章节中，我们将详细探讨SVPWM的工作原理、理论基础、算法解析等关键内容，并结合实际应用分析其面临的挑战和优化策略。通过深入理解SVPWM技术，我们可以更好地应对技术的未来发展趋势，并有效推动相关领域的技术革新。

# 2. SVPWM理论基础与算法解析

## 2.1 SVPWM的工作原理

### 2.1.1 空间矢量理论简介
空间矢量脉宽调制（Space Vector Pulse Width Modulation, SVPWM）是一种先进的电机驱动控制技术，其核心思想是将三相逆变器看作一个能够产生旋转磁场的装置。通过合理控制逆变器开关器件的通断，可以合成出任意空间位置和幅值的三相对称电压，用以驱动电机。

将传统的两相静止坐标系电压矢量转换为旋转坐标系下的矢量，可以得到与实际电动机电磁状态更接近的描述，这有利于提高控制精度和系统的动态响应性能。空间矢量理论将三相交流电压源逆变器的开关状态抽象为八种基本空间矢量，再加上零矢量，共九种矢量。这九种矢量能够组合形成一个完整的圆形或椭圆形的旋转矢量，用于精确地控制电机的电压和频率。

### 2.1.2 SVPWM与传统PWM的比较
SVPWM与传统正弦脉宽调制（SPWM）相比，在相同开关频率下，SVPWM能够输出更高的有效值电压，从而提高电机的效率和功率密度。在空间矢量控制下，开关器件的开关次数更少，因此开关损耗和电磁干扰（EMI）也会相应减少。

表 2.1 展示了SVPWM与传统PWM技术的对比情况。

| 特性 | SVPWM | 传统PWM |
|------|-------|----------|
| 电压利用率 | 高 | 较低 |
| 开关频率 | 较低 | 较高 |
| 磁链轨迹 | 接近圆形 | 椭圆形 |
| 控制复杂性 | 较高 | 较低 |
| 开关损耗 | 较低 | 较高 |
| 谐波含量 | 较少 | 较多 |

通过这张表，我们可以看到SVPWM技术在提高电压利用率和减少开关损耗方面的优势。但同时，也必须注意SVPWM的控制算法相对更复杂，需要更精确的控制和计算。

## 2.2 SVPWM的数学模型

### 2.2.1 坐标变换的基本概念
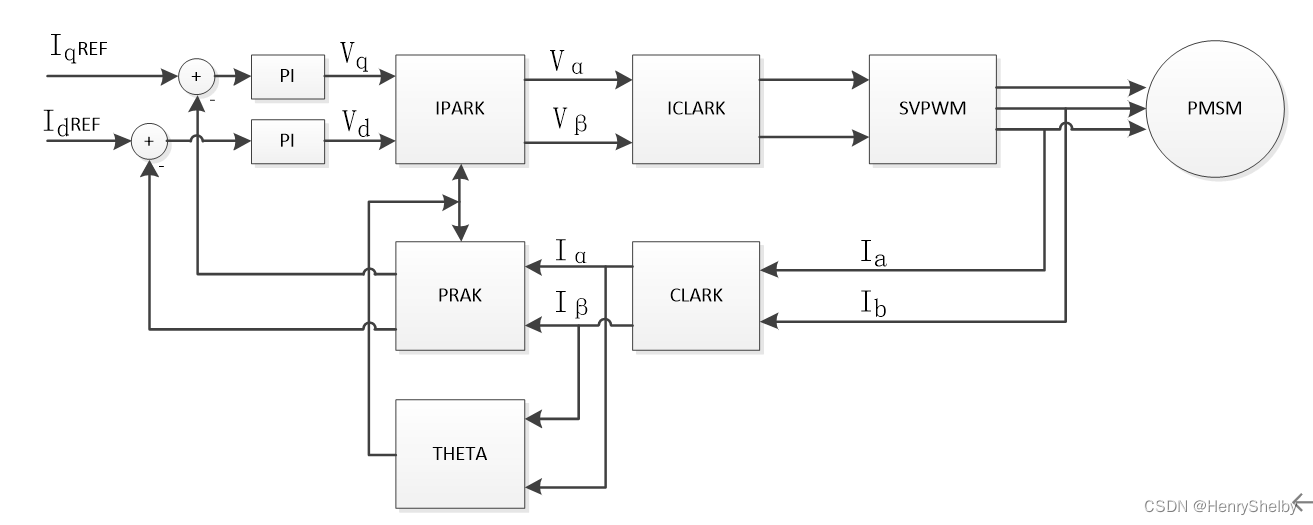
SVPWM技术的实现，需要在不同的坐标系之间进行转换，如将三相静止坐标系转换到两相旋转坐标系。常用的是Clarke变换和Park变换。

Clarke变换将三相静止坐标系下的电压值\(V_a, V_b, V_c\)转换为两相静止坐标系下的\(V_\alpha, V_\beta\)。其变换矩阵如下：

\[ \begin{bmatrix} V_\alpha \\ V_\beta \end{bmatrix} = \begin{bmatrix} 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} V_a \\ V_b \\ V_c \end{bmatrix} \]

Park变换则进一步将\(V_\alpha, V_\beta\)变换到两相旋转坐标系中的\(V_d, V_q\)，其中\(V_d\)为直轴分量，\(V_q\)为交轴分量。这一步需要用到电机旋转速度参数，变换矩阵如下：

\[ \begin{bmatrix} V_d \\ V_q \end{bmatrix} = \begin{bmatrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} V_\alpha \\ V_\beta \end{bmatrix} \]

### 2.2.2 SVPWM的数学表示
SVPWM可以看作是基于矢量控制理论的一种PWM技术。基本的数学表示为：

\[ V_{s} = T_1 \cdot V_{1} + T_2 \cdot V_{2} + T_0 \cdot V_{0} \]

其中，\(V_{s}\)为合成矢量，\(V_{1}\)和\(V_{2}\)为相邻的非零矢量，\(V_{0}\)为零矢量。\(T_1\)、\(T_2\)和\(T_0\)分别为对应矢量的时间占空比，它们的和为一个PWM周期。

## 2.3 SVPWM算法的实现步骤

### 2.3.1 参考矢量的确定
首先，需要确定参考矢量\(V_{ref}\)，这通常是通过电机控制算法（如矢量控制或直接转矩控制）