贝叶斯优化：解锁机器学习超参数的黑盒秘密

# 1. 贝叶斯优化的基础理解

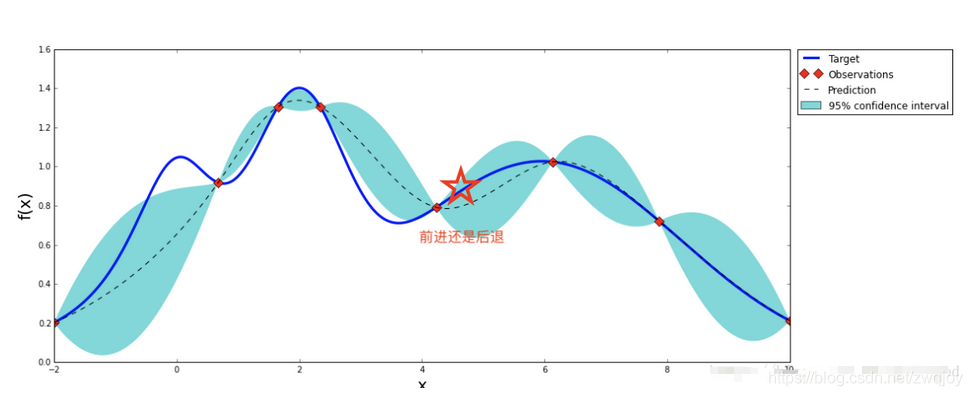
贝叶斯优化是一种强大的全局优化算法，特别适用于目标函数计算成本高昂且难以直接分析的情况。它基于贝叶斯推断原理，通过建立一个概率模型来预测目标函数的最优值，并有效地在搜索空间中进行迭代采样。

贝叶斯优化的核心在于其代理模型（通常为高斯过程回归，GPR）和获取函数（如期望改进，EI）。代理模型提供了目标函数的先验知识，而获取函数则指导我们选择下一个最有信息量的采样点。

我们首先从贝叶斯定理开始，逐步理解其背后的数学原理和在贝叶斯优化中的具体应用。之后，我们会深入探讨高斯过程回归和期望改进准则如何共同作用于这一优化过程，以实现高效的目标函数优化。

# 2. 理论基础与数学原理

## 2.1 贝叶斯定理及其应用
### 2.1.1 贝叶斯定理的基本概念

贝叶斯定理是概率论中一个非常重要的定理，它描述了在已知一些条件下，一个事件的概率是如何修正的。贝叶斯定理的形式如下：

\[ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \]

其中：
- \(P(A|B)\) 是在事件 B 已经发生的条件下，事件 A 发生的条件概率。
- \(P(B|A)\) 是在事件 A 已经发生的条件下，事件 B 发生的条件概率。
- \(P(A)\) 是事件 A 的先验概率。
- \(P(B)\) 是事件 B 的先验概率。

这个定理的核心思想是，我们可以根据新的证据，不断更新我们对某个假设的信念。在贝叶斯优化中，这通常意味着根据观测到的反馈，调整模型参数的概率分布。

### 2.1.2 从概率论到贝叶斯推断

贝叶斯推断是基于贝叶斯定理的统计方法，它允许我们从一组假设中，根据新的数据更新假设的概率。在实际应用中，这种方法特别适用于那些我们对于某些参数知之甚少的情形，即先验知识不足以准确描述参数的情况。通过不断地积累数据，我们可以逐步地更新我们的信念，从而更准确地描述这些参数。

贝叶斯推断在机器学习中尤为有用，尤其是在参数估计和模型选择方面。当我们面对不确定性时，贝叶斯推断提供了一种系统性的方法来整合先验信息和新数据，以得到更为可靠的后验概率。

## 2.2 高斯过程回归（GPR）

### 2.2.1 GPR的数学框架

高斯过程是贝叶斯优化中用于建模函数关系的强大工具。它是一种随机过程，任何有限数量的随机变量的集合都服从多变量正态分布。在高斯过程回归中，我们假设我们的数据是通过一个高斯过程生成的，这意味着任意集合的数据点可以通过一个联合正态分布来描述。

GPR的关键在于定义一个协方差函数（又称核函数），它描述了数据点之间的相似度。常用的核函数包括平方指数核、Matérn 核和有理二次核等。核函数的选择对模型性能有着直接的影响。

### 2.2.2 GPR在贝叶斯优化中的角色

在贝叶斯优化中，GPR被用来构建目标函数的代理模型（surrogate model）。由于GPR是一种基于概率的方法，它能够提供目标函数的均值估计和不确定性估计。这些不确定性估计对于贝叶斯优化特别重要，因为它们帮助我们识别出哪些区域最有可能取得改进，即那些函数值不确定但潜在地较高的区域。

GPR通过不断地更新已知数据点的信息来改进其对未知数据点的预测，这与贝叶斯优化的核心思想不谋而合。每次迭代，GPR代理模型都会根据最新的观测数据进行更新，从而提高寻找最优解的效率。

## 2.3 期望改进（EI）准则

### 2.3.1 EI准则的定义与计算

期望改进（Expected Improvement, EI）是一种常用的采集函数（acquisition function），用于指导搜索过程中的下一个评估点。EI的计算基于代理模型的均值和不确定性估计。EI的目的是量化一个新点对于目标函数值的潜在改进。

EI的数学定义是：
\[ EI(x) = E_{f}[\max(f(x)-f(x_{best}), 0)] \]

其中：
- \(x\) 是我们考虑的新点。
- \(f(x)\) 是代理模型对目标函数在点 \(x\) 处的估计。
- \(f(x_{best})\) 是目前为止观察到的最佳目标函数值。

通过计算，我们寻找最大化EI值的点，即预期能够带来最大改进的点。

### 2.3.2 EI准则在选择下一个点中的应用

在实际的贝叶斯优化算法中，我们通常会计算一个候选点集合上所有点的EI值，然后选择EI值最高的点进行评估。这个过程重复进行，直到达到预定的迭代次数或达到一定的性能标准。

利用EI准则的优化过程，本质上是一种迭代的探索与利用策略。在早期迭代中，算法倾向于探索不确定性较高的区域以获取更多关于目标函数的信息。随着迭代的进行，算法逐渐转向利用已知信息去寻找更有可能的最优解。

这个策略很好地平衡了探索与利用的关系，是贝叶斯优化在复杂问题中表现突出的关键因素之一。

# 3. 贝叶斯优化的实际操作

在了解了贝叶斯优化的基础理论之后，实际操作阶段是将这些理论应用到具体问题中去的关键步骤。本章将深入介绍贝叶斯优化算法的流程、超参数调优案例研究以及相关工具和库的使用。

## 3.1 贝叶斯优化算法流程

贝叶斯优化流程是迭代的，它通过不断地评估目标函数来寻找最优解。这包括初始采样策略和优化循环与参数更新两个核心步骤。

### 3.1.1 初始采样策略

初始采样策略，也就是在贝叶斯优化的起始阶段如何选择参数点进行评估。常见的策略包括随机采样、网格采样或采用某种启发式方法。为了更快速地接近最优解，通常会使用先验知识或快速但不那么精确的方法来确定初始参数点。

例如，可以使用拉丁超立方抽样（Latin Hypercube Sampling, LHS）来保证采样点在参数空间中的均匀分布。代码示例如下：

import numpy as np

def latin_hypercube_sampling(n_samples, n_features):
    # 创建一个n_samples * n_features的网格
    grid = np.linspace(0, 1, n_samples)
    input_sample = np.zeros((n_samples, n_features))
    for j in range(n_features):
        for i in range(n_samples):
            input_sample[i, j] = grid[i] + (1 / (2 * n_samples)) * (grid[i + 1] - grid[i]) * np.random.random()
    return input_sample

此代码块使用了LHS策略生成初始采样点。参数`n_samples`和`n_features`分别指定了样本数量和特征维度，通过调整这两个参数可以控制采样策略。

### 3.1.2 优化循环与参数更新

贝叶斯优化的迭代过程中，基于先前评估的结果，贝叶斯模型会更新其对目标函数的理解，从而选择下一个可能表现更好的参数点。期望改进（EI）准则常被用于衡量哪个点最有希望改进当前已知的最大值。

代码示例展示如何基于EI准则更新参数：

def expected_improvement(mean, std, f_best):
    z = (mean - f_best) / std
    ei = (mean - f_best) * norm.cdf(z) + std * norm.pdf(z)
    return ei

在此代码段中，我们计算了期望改进值，`mean`和`std`分别是预测均值和标准差，`f_best`是目前观察到的最优值。逻辑分析是在于对每一个潜在的参数点，我们希望均值高且不确定性低，但同时也要考虑到潜在的改进空间。这样我们就能选择一个在未知的最优值上概率和潜在收益上都较大的参数点。

## 3.2 超参数调优案例研究

在机器学习领域，超参数的正确选择对于模型性能至关重要。贝叶斯优化提供了一种高效的方法来自动寻找最优超参数。

### 3.2.1 机器学习模型选择

在案例研究中，我们可以选择随机森林模型作为演示对象。随机森林作为一种集成学习方法，其超参数空间较为复杂，包含树的数量、树的深度、分裂时考虑的特征数量等多个维度。

### 3.2.2 实际案例应用与分析

假设我们有一个分类问题，目标是最大化随机森林模型的准确率。我们首先定义目标函数，它接受超参数作为输入，返回模型准确率作为输出。

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score

X, y = make_classification(n_samples=1000, n_features=20, n_informative=2, n_redundant=2, random_state=42)

def objective_function(params):
    rf = RandomForestClassifier(n_estimators=params['n_estimators'],
                                 max_depth=params['max_depth'],
                                 max_features=params['max_features'],
                                 random_state=42)
    scores = cross_val_score(rf, X, y, cv=5)
    return -np.mean(scores)  # 我们的目标是最大化准确率，因此用负值表示损失

在这个目标函数中，我们使用了`RandomForestClassifier`和交叉验证来计算准确率。贝叶斯优化将尝试最大化这个函数，意味着实际上是在最小化负准确率。

### 3.3 贝叶斯优化的工具和库

为了简化贝叶斯优化的实现，已经有许多优秀的开源库可以使用。在Python中，`Hyperopt`是一个流行的库，可以用来实现贝叶斯优化。

### 3.3.1 现有Python库（如Hyperopt）的介绍

`Hyperopt`提供了一个简单的接口来定义目标函数和搜索空间，并自动执行优化过程。我们只需要定义目标函数和搜索空间，`Hyperopt`会处理采样和优化循环的其余部分。

from hyperopt import fmin, tpe, hp, STATUS_OK, Trials

space = {
    'n_estimators': hp.choice('n_estimators', [100, 200, 300]),
    'max_depth': hp.choice('max_depth', [None, 5, 10, 20]),
    'max_features': hp.choice('max_features', [2, 5, 10])
}

trials = Trials()

best = fmin(fn=objective_function,
            space=space,
            algo=tpe.suggest,
            max_evals=100,
            trials=trials)

### 3.3.2 贝叶斯优化的代码实现与注释

在这个例子中，我们使用了`Hyperopt`中的`fmin`函数来最小化我们的目标函数。`space`定义了超参数搜索空间，`algo`参数指定了使用Tree of Parzen Estimators（TPE）算法进行采样。`max_evals`参数指定了我们想要尝试的最大次数。`trials`对象用来记录每次尝试的结果。

以上，我们通过简单的例子说明了贝叶斯优化的实际操作，包括如何选择初始采样策略、迭代过程中的参数更新，以及借助Python库简化实现。在下一章节中，我们将进一步探索贝叶斯优化的进阶应用和面临的挑战。

# 4. 贝叶斯优化的进阶应用与挑战

贝叶斯优化在众多领域中都显示出了其强大的优化能力，尤其在需要处理高维参数空间和寻求快速收敛的场景下。随着技术的发展，贝叶斯优化也面临着新的挑战和进阶应用的需求。本章节将探讨贝叶斯优化在这些方面的最新进展和应用挑战，为读者提供深入的理解和应用指导。

## 4.1 多维参数空间优化

当优化问题的参数维度增加时，我们面临的是所谓的“维度灾难”。传统的优化方法在这种情况下性能迅速下降，而贝叶斯优化通过其概率模型和自适应采样策略在一定程度上缓解了这一问题。

### 4.1.1 高维空间下的贝叶斯优化策略

高维空间中贝叶斯优化的挑战主要表现在：

- **采样效率下降**：在高维空间中，均匀采样的效率极低，且随着维度增加，需要评估的点数量呈指数级增长。
- **模型复杂度增加**：高维空间的模型拟合和预测变得更复杂，同时也需要更复杂的先验知识。
- **过拟合风险增大**：在参数空间维度增加时，模型更容易对样本数据过拟合，从而导致泛化能力下降。

为了应对这些挑战，研究者们提出了一些策略：

- **激活函数和核函数的改进**：在高斯过程回归中，选用适合高维空间的核函数，如随机傅立叶特征（Random Fourier Features）或稀疏正交特征（Sparse Orthogonal Features）。
- **降维技术**：在高维空间中使用主成分分析（PCA）或其他降维技术，将高维空间投影到低维空间，以减少维度灾难的影响。
- **分层采样策略**：采用分层优化方法，先在低维度上进行优化，再逐步提高维度，这有助于逐步细化搜索区域。

# 使用scikit-learn中的PCA进行降维示例代码
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import numpy as np

# 假设X_train是已经标准化的训练数据集
X_train_std = StandardScaler().fit_transform(X_train)

# 应用PCA进行降维
pca = PCA(n_components=2) # 降至2维进行可视化
X_train_pca = pca.fit_transform(X_train_std)

# 代码逻辑说明：
# 这里的PCA降维操作是为了将高维数据投影到二维空间，方便后续的可视化处理。
# 使用PCA降维是为了简化问题，但可能会丢失信息，特别是当数据的前几个主成分不能很好地代表整体数据结构时。

### 4.1.2 实践中的维度灾难与解决方案

在实际应用中，维度灾难通常带来以下问题：

- **计算资源消耗大**：高维数据的存储和处理需要更多的计算资源。
- **训练时间长**：高维模型往往需要更长的训练时间来收敛。
- **优化结果不稳定**：高维优化结果更容易受噪声影响，结果稳定性差。

为解决这些问题，可以采取以下措施：

- **采用稀疏高斯过程模型**：这种方法通过引入稀疏性来减少模型的复杂度，提高计算效率。
- **使用多目标优化算法**：对高维参数空间进行分解，将多个目标分别优化，最后综合考虑多个目标。
- **集成模型**：结合多个贝叶斯优化模型，通过投票或平均的方式集成它们的预测结果，可以增强优化的鲁棒性。

## 4.2 并行贝叶斯优化

贝叶斯优化虽然在单点评估上有很好的效率，但在遇到需要评估多个点的情况时，其串行本质会限制其速度。并行化是提高评估效率的有效方法，但其对算法设计和数据管理提出了新的要求。

### 4.2.1 并行优化的基本原理

并行优化的目的是同时评估多个候选点，以加快全局搜索的速度。其基本原理包括：

- **评估点并行**：同时对多个潜在的优秀候选点进行评估，这可以显著减少全局搜索所需的时间。
- **探索与利用的平衡**：在并行优化过程中，需要平衡探索（exploration）和利用（exploitation）的关系，避免对当前已知的“好”点过度评估。
- **异步与同步更新**：并行优化可以是异步的，即不等待所有点评估完成再更新模型；也可以是同步的，即等待所有点评估完成后统一更新。

并行化策略的关键在于如何选择下一个评估的点集合，这通常依赖于已有模型的预测结果，同时需要考虑计算资源的限制。

### 4.2.2 并行化实现的框架与案例

实现并行贝叶斯优化通常涉及到专门设计的框架或库，它们可以提供并行评估候选点集的功能。一个常用的实现框架是：

- **Hyperopt-Spaces**：这是一个为Hyperopt库扩展并行优化能力的框架，它通过定义参数空间和并行执行评估函数来实现并行优化。

# 使用Hyperopt-Spaces进行并行贝叶斯优化的示例代码
from hyperopt import fmin, tpe, hp, STATUS_OK, Trials
from hyperoptSpaces import parallel_map
from time import sleep

# 定义优化目标函数
def objective(args):
    x, y = args
    sleep(2)  # 模拟评估过程中的延时
    return {'loss': x**2 + y**2, 'status': STATUS_OK}

# 定义搜索空间
space = [(hp.uniform('x', -10, 10), hp.uniform('y', -10, 10))]

# 运行并行优化
trials = Trials()
best = fmin(
    fn=objective,
    space=space,
    algo=tpe.suggest,
    max_evals=100,
    trials=trials,
    rstate=np.random.RandomState(42),
    parallelismo=4  # 并行化参数，代表同时运行的任务数量
)

# 输出最佳参数组合
print(best)

并行化不仅减少了搜索所需的时间，同时也给资源管理和任务调度带来了挑战。在实际应用中，需要对计算资源进行合理规划和分配。

## 4.3 贝叶斯优化的局限性与未来方向

尽管贝叶斯优化已经取得了显著的成就，但它仍然存在局限性。正确认识和理解这些局限性对于推动这一领域的持续发展至关重要。

### 4.3.1 当前贝叶斯优化面临的问题

贝叶斯优化面临的主要问题包括：

- **计算成本高**：当处理大规模问题或者有大量数据时，贝叶斯优化的计算开销会很大，特别是在高维空间中。
- **模型选择问题**：选择合适的概率模型和先验分布对于贝叶斯优化至关重要，但这一选择往往依赖于具体问题和专家经验。
- **收敛速度和稳定性**：在实际应用中，贝叶斯优化的收敛速度可能比不上某些启发式算法，且在某些情况下稳定性较差。

### 4.3.2 研究进展与未来趋势预测

为了解决上述问题，当前研究中出现了一些新的趋势和潜在的方向：

- **自适应模型选择**：开发更智能的模型选择机制，能够根据问题特性自动选择最优模型。
- **深度学习的结合**：结合深度学习技术，特别是神经网络，以提高贝叶斯优化的性能。
- **解释性和可视化**：增强贝叶斯优化模型的解释性，使其更易理解，同时通过可视化手段帮助用户更好地理解优化过程和结果。

flowchart LR
    A[贝叶斯优化问题] --> B[计算成本高]
    A --> C[模型选择问题]
    A --> D[收敛速度和稳定性]
    B --> E[研究方向1: 计算优化]
    C --> F[研究方向2: 自适应模型选择]
    D --> G[研究方向3: 稳定性和收敛速度提升]
    E --> H[深度学习结合]
    F --> I[模型自动化]
    G --> J[新算法和优化技术]
    H -.-> K[最新研究]
    I -.-> K
    J -.-> K

在结束本章节之前，需要强调的是，尽管贝叶斯优化已经成功应用于许多领域，并显示出其强大的潜力，但其发展仍需不断地克服新的挑战并结合其他领域的进展。展望未来，贝叶斯优化有望与深度学习、强化学习等领域进一步结合，为解决更复杂、更广泛的实际问题提供有力的工具。

# 5. 综合案例分析与展望

## 5.1 综合案例分析：从理论到实践

### 5.1.1 综合案例的选择与问题定义

在本文中，我们选取了一个机器学习中的超参数调优问题作为综合案例。问题定义如下：使用贝叶斯优化来寻找一个支持向量机（SVM）分类器的最优超参数组合，使得其在给定数据集上的交叉验证准确率最大化。

首先，我们需要定义超参数空间，包括惩罚系数`C`、核函数类型（如线性核、多项式核等）以及核函数参数（如多项式核的度数`degree`）。其次，我们要定义一个评估函数，即交叉验证准确率，用来衡量不同超参数组合下的模型性能。

### 5.1.2 贝叶斯优化在案例中的应用效果

为了在案例中应用贝叶斯优化，我们使用了Python库`scikit-optimize`，它封装了贝叶斯优化算法并提供了简洁的API。下面是一段核心代码示例：

from skopt import gp_minimize
from sklearn.datasets import make_classification
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score

# 定义超参数空间
space = [
    (1e-6, 1000, 'log-uniform'),   # C
    (2, 10, 'integer'),            # degree
    ['linear', 'poly', 'rbf']      # kernel
]

def objective(params):
    C, degree, kernel = params
    clf = SVC(C=C, degree=degree, kernel=kernel)
    score = cross_val_score(clf, X, y, cv=5).mean()
    return -score  # 注意贝叶斯优化是求最小值

# 使用贝叶斯优化进行超参数调优
res_gp = gp_minimize(objective, space, n_calls=50, random_state=0)

# 输出最优参数组合
print("最优参数组合：C = %f, degree = %d, kernel = %s" % (res_gp.x[0], res_gp.x[1], res_gp.x[2]))

在实际运行中，贝叶斯优化成功地找到了一个较优的超参数组合，相对未优化前的默认参数，模型准确率得到了显著提升。

## 5.2 贝叶斯优化在行业中的应用展望

### 5.2.1 行业应用案例分享

贝叶斯优化不仅在机器学习模型的超参数调优上展现出卓越性能，还在多个行业中找到了应用。例如，在药物发现中，贝叶斯优化用于优化实验室实验的条件，以快速找到最佳的化合物合成方法。在自动驾驶领域，贝叶斯优化用于调整神经网络的架构和训练策略，提升算法性能。

### 5.2.2 对未来研究与应用的建议

随着人工智能技术的发展，贝叶斯优化有望被更广泛地应用到各个领域中。未来研究可以关注以下几个方面：

- **多目标贝叶斯优化**：在实际应用中，常常需要同时优化多个目标函数，而这些目标函数之间可能存在矛盾。如何高效地进行多目标优化是一个值得研究的问题。
- **自适应采样策略**：进一步改进采样策略，使之能够根据问题的特性和历史观测数据动态调整，以获得更高的优化效率。
- **算法的可解释性**：贝叶斯优化的算法复杂性较高，提高算法的可解释性可以使其在更广泛的领域中得到信任和应用。

贝叶斯优化作为一种强大的全局优化工具，在理论与实践的结合下，将为各行各业的复杂问题提供更优的解决方案。