Java数据结构精讲：图遍历算法与数据结构的完美结合

# 1. 图数据结构的理论基础

在计算机科学领域，图数据结构是表示对象间复杂关系的强有力工具。它由节点（顶点）和连接节点的边组成，能够直观地表达现实世界中的多种关系，例如社交网络中的朋友关系、网络中的路由路径、以及交通网络中的道路系统等。

## 1.1 图的定义和基本术语

图G由一组顶点V和一组边E组成，通常可以表示为G=(V, E)。顶点表示图中的实体，而边则表示这些实体之间的关联关系。如果图中的边具有方向，则称为有向图；反之，如果边是无方向的，那么该图就称为无向图。此外，边的权重（权重可以表示距离、成本等）也可以被引入到图的定义中，形成加权图。

## 1.2 遍历算法的重要性

图的遍历算法是探索图结构中每个顶点的基本方法。它们是很多复杂算法的基石，例如最短路径算法、网络流分析以及深度优先搜索（DFS）和广度优先搜索（BFS）。掌握了遍历算法，可以更加深入地理解图的结构，为后续的高级图算法学习和应用打下坚实的基础。

# 2. 图的遍历算法深度解析

### 2.1 图的遍历算法概述

在探讨图数据结构时，遍历算法是构建各种图算法的基础。为了全面掌握图遍历的精髓，我们首先需要从图的基本定义和术语开始。

#### 2.1.1 图的定义和基本术语

图是由一组顶点（也称为节点）和一组连接这些顶点的边组成的。顶点间的连线表示它们之间的某种关系。在无向图中，边是没有方向的，而在有向图中，边是有方向的，由一个顶点指向另一个顶点。图可以表示为G = (V, E)，其中V是顶点的集合，E是边的集合。

除了基本概念外，图论中的重要术语还包括：

- **路径**：顶点序列，其中每对相邻顶点间都有边相连。
- **环**：路径的起点和终点是同一个顶点的特殊路径。
- **连通**：在无向图中，如果两个顶点间存在路径，则称这两个顶点是连通的。
- **强连通**：在有向图中，如果两个顶点间可以互相到达，则称这两个顶点是强连通的。
- **邻接**：如果两个顶点之间存在一条边，则称它们是邻接的。

#### 2.1.2 遍历算法的重要性

图的遍历算法可以分为两类：深度优先搜索（DFS）和广度优先搜索（BFS）。遍历算法重要性体现在多个方面：

- **发现图的所有顶点**：遍历算法可以访问图中的每个顶点一次。
- **路径搜索**：在有向无环图（DAG）中，遍历算法可以用来找到从起点到终点的所有可能路径。
- **拓扑排序**：BFS可以用于对有向无环图进行拓扑排序。
- **解决实际问题**：如网络爬虫、社交网络分析等实际问题中，图的遍历算法都扮演着核心角色。

### 2.2 深度优先搜索(DFS)

#### 2.2.1 DFS的基本思想和实现

深度优先搜索是一种用于图遍历的算法，它尽可能深地搜索图的分支。当节点v的所在边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这个过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，深度优先搜索将从另一个源节点开始，重复这一过程，直到所有节点都被探寻。

下面是DFS的伪代码实现：

DFS(v)
  if v 是未访问的
    标记 v 为已访问
    对于 v 的每一个邻接点 w
      DFS(w)

#### 2.2.2 DFS的应用实例分析

假设我们有一个无向图，我们需要用DFS来找出图中所有的连通分量。可以定义一个辅助函数`DFSUtil`来进行深度优先搜索，并使用一个数组来记录每个顶点的访问状态。下面是一个简化的例子，展示了如何使用DFS来解决这个问题：

public class Graph {
    private int V;   // 顶点的数量
    private LinkedList<Integer> adj[]; // 邻接表

    public Graph(int v) {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }

    public void addEdge(int v, int w) {
        adj[v].add(w); // 在顶点v的邻接表中添加顶点w
        adj[w].add(v); // 在顶点w的邻接表中添加顶点v
    }

    // DFS函数，用于找出所有连通分量
    private void DFSUtil(int v, boolean visited[]) {
        visited[v] = true;
        System.out.print(v + " ");

        Iterator<Integer> i = adj[v].listIterator();
        while (i.hasNext()) {
            int n = i.next();
            if (!visited[n])
                DFSUtil(n, visited);
        }
    }

    // 该函数用于找出所有连通分量，并打印它们
    public void fillOrder(int v, boolean visited[], Stack stack) {
        visited[v] = true;
        Iterator<Integer> i = adj[v].listIterator();
        while (i.hasNext()) {
            int n = i.next();
            if (!visited[n])
                fillOrder(n, visited, stack);
        }
        stack.push(v);
    }
}

### 2.3 广度优先搜索(BFS)

#### 2.3.1 BFS的原理和步骤

广度优先搜索是一种用于图的层次遍历算法。从一个顶点开始，先访问它的所有邻接点，然后对每个邻接点执行相同的策略。与DFS不同，BFS使用队列数据结构来跟踪访问过的顶点。

BFS的伪代码如下：

BFS(s)
  创建一个空队列 Q
  Q.enqueue(s) // 将源顶点入队列
  while Q 不为空 do
    v = Q.dequeue() // 出队列
    if v 未被访问 then
      标记 v 为已访问
      for v 的所有邻接点 w do
        Q.enqueue(w) // 将所有未访问的邻接点入队列

#### 2.3.2 BFS的效率分析与优化

BFS的效率主要取决于队列操作的次数。在最坏情况下，每个顶点和每条边都会被访问一次，因此时间复杂度为O(V+E)，其中V是顶点数，E是边数。空间复杂度则由队列的大小决定，最坏情况下也是O(V)。

BFS的优化可以从几个方面考虑：

- **优化存储空间**：在稠密图中使用邻接矩阵，而在稀疏图中使用邻接表。
- **避免冗余操作**：可以在访问顶点时将其标记，避免重复访问。
- **并行处理**：在多核处理器上，可以并行化BFS的某些部分，如并行处理顶点的邻接列表。

以下是一个BFS算法在Java中的实现示例：

public class BFSExample {
    private int vertices;   // 顶点数量
    private LinkedList<Integer> adj[]; // 邻接表

    public BFSExample(int vertices) {
        this.vertices = vertices;
        adj = new LinkedList[vertices];
        for (int i = 0; i < vertices; ++i)
            adj[i] = new LinkedList();
    }

    public void addEdge(int v, int w) {
        adj[v].add(w);
    }

    public void breadthFirstSearch(int s) {
        boolean visited[] = new boolean[vertices];

        LinkedList<Integer> queue = new LinkedList<>();

        visited[s] = true;
        queue.add(s);

        while (queue.size() != 0) {
            s = queue.poll();
            System.out.print(s + " ");

            Iterator<Integer> i = adj[s].listIterator();
            while (i.hasNext()) {
                int n = i.next();
                if (!visited[n]) {
                    visited[n] = true;
                    queue.add(n);
                }
            }
        }
    }
}

在这段代码中，我们创建了一个`BFSExample`类来表示图，并使用邻接表`adj`来存储图中的边。我们定义了`addEdge`方法来添加边，并在`breadthFirstSearch`方法中实现了BFS算法。这个方法首先标记起始顶点为已访问，然后将其加入队列。之后，它将重复执行以下步骤，直到队列为空：从队列中取出一个顶点，打印它，并将其所有未访问的邻接点加入队列并标记为已访问。

通过这些实例，我们可以了解到DFS和BFS算法在解决图遍历问题中的重要性和实现方式。接下来的章节将介绍如何在Java中具体实现这些算法，并分析如何对遍历过程进行优化。

# 3. 图数据结构在Java中的实现

图数据结构的实现方式直接影响了其遍历效率和应用场景。在这一章节中，我们将深入探讨图的表示方法，并专注于Java语言中的实现。我们不仅会展示基础的实现代码，还会分析各种优化策略，从而提供高效且可扩展的图数据结构解决方案。

## 3.1 Java中的图表示方法

### 3.1.1 邻接矩阵与邻接表的对比

在图的实现中，最常见的方式是邻接矩阵和邻接表。每种方法都有其优缺点，适用于不同的使用场景。

- **邻接矩阵**表示图是通过二维数组实现的，其中数组中的每个元素表示节点之间的连接状态。它适合表示稠密图，但空间复杂度较高。

int[][] adjacencyMatrix = new int[n][n]; // n为节点数量

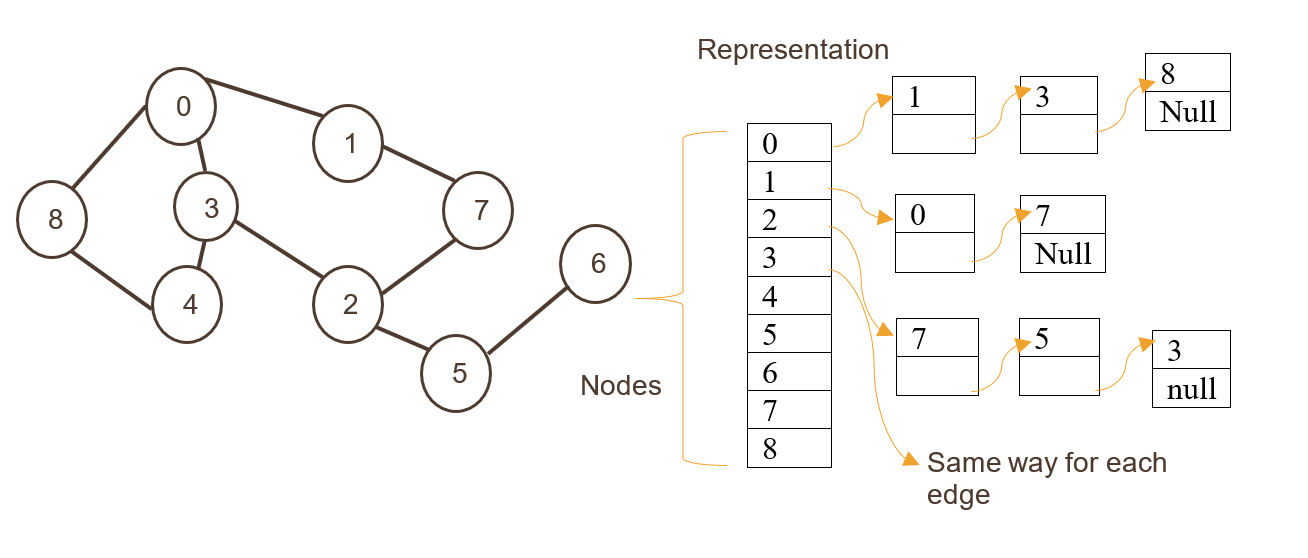
- **邻接表**通过链表或者数组的数组来实现，每个节点都有一个列表，列表中的每个元素指向与之相邻的节点。它更适合稀疏图，空间复杂度较低。

List<Integer>[] adjacencyList = new List[n];
for (int i = 0; i < n; i++) {
    adjacencyList[i] = new ArrayList<>();
}

### 3.1.2 Java中图的数据结构定义

在Java中，我们通常会定义一个类来表示图，其中包含图的数据结构以及相关操作。

public class Graph {
    private int numVertices; // 节点数量
    private LinkedList<Integer>[] adjacencyList; // 邻接表

    public Graph(int numVertices) {
        this.numVertices = numVertices;
        adjacencyList = new LinkedList[numVertices];
        for (int i = 0; i < numVertice