Java数据结构与算法复习：AVL树、红黑树与平衡化技术

# 1. 数据结构与算法基础回顾

## 1.1 什么是数据结构与算法
在计算机科学中，数据结构是组织和存储数据的一种方式，它旨在支持特定的算法效率。算法是一系列定义明确的操作步骤，用于解决特定的问题或执行特定的任务。

## 1.2 算法效率
算法效率通常通过时间复杂度和空间复杂度来衡量。时间复杂度反映了算法执行时间随输入数据规模增长的变化趋势，而空间复杂度则描述了算法执行过程中所占用的存储空间。

## 1.3 常见的数据结构
数据结构包括基本类型（如数组、链表）和复杂类型（如栈、队列、树、图）。基本类型用于存储数据集合，复杂类型则定义了数据元素之间的关系和操作。

## 1.4 算法示例：排序和搜索
排序算法如冒泡排序、快速排序、归并排序等，以及搜索算法如二分搜索，都是数据结构与算法基础中的重要组成部分，它们是理解和应用数据结构的基础。

本章简要回顾了数据结构与算法的基础知识，为后续章节中深入探讨AVL树、红黑树等高级数据结构及其平衡化技术奠定了基础。在接下来的内容中，我们将深入探讨这些高级数据结构如何在不同的应用场景中维持平衡，并优化性能。

# 2. AVL树详解与应用

### 2.1 AVL树的定义和特性
AVL树是一种自平衡的二叉搜索树，它在每个节点上增加了平衡因子来保持树的平衡。AVL树的平衡性通过确保任一节点的左右子树的高度差不超过1来实现，这就保证了AVL树在最坏情况下的时间复杂度接近于O(log n)。

#### 2.1.1 平衡二叉树的概念
在二叉搜索树（BST）中，如果一个节点的左右子树高度差超过1，则被认为是不平衡的。平衡二叉树（Balanced Binary Tree）要求树上任一节点的左子树和右子树的高度差最多为1。由于这种树结构可以避免二叉搜索树在最坏情况下的性能下降，它成为了一种实用且高效的数据结构。

#### 2.1.2 AVL树的平衡因子和平衡条件
AVL树的平衡因子是通过检查节点的左子树高度和右子树高度的差来确定的。一个节点的平衡因子定义为：

平衡因子 = 高度(左子树) - 高度(右子树)

对于AVL树中的每个节点，它的平衡因子只能是-1、0或1。如果某个节点的平衡因子不在这个范围内，就需要进行旋转操作来重新平衡树。

### 2.2 AVL树的旋转操作
旋转是AVL树平衡调整的核心操作，分为单旋转和双旋转。单旋转包括左旋和右旋，而双旋转包括左右双旋和右左双旋。旋转操作的目的是重新分配节点，使树达到平衡状态。

#### 2.2.1 单旋转与双旋转的原理
单旋转操作只涉及一个节点和它的子节点，而双旋转则是结合两个单旋转操作来解决某些更复杂的不平衡情况。

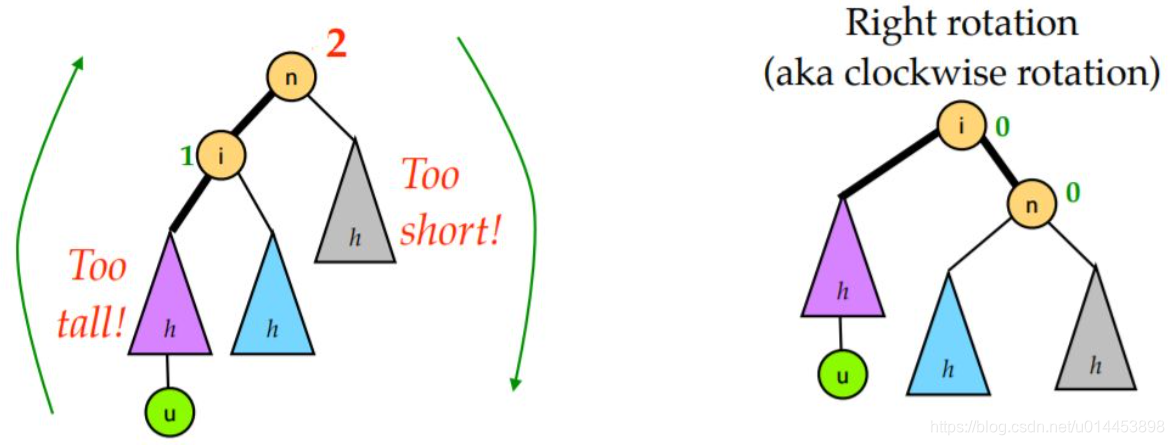
- **左旋操作**：将右子节点上升为父节点，原父节点降级为右子节点。
- **右旋操作**：将左子节点上升为父节点，原父节点降级为左子节点。
- **左-右双旋**：先对左子节点执行左旋，然后对原节点执行右旋。
- **右-左双旋**：先对右子节点执行右旋，然后对原节点执行左旋。

#### 2.2.2 旋转操作的代码实现
下面是一个左旋操作的代码示例，该操作涉及到旋转节点的左右子节点：

struct AVLNode {
    int key;
    int height;
    struct AVLNode *left;
    struct AVLNode *right;
};

struct AVLNode* leftRotate(struct AVLNode* x) {
    struct AVLNode* y = x->right;
    struct AVLNode* T2 = y->left;

    // Perform rotation
    y->left = x;
    x->right = T2;

    // Update heights
    x->height = max(getHeight(x->left), getHeight(x->right)) + 1;
    y->height = max(getHeight(y->left), getHeight(y->right)) + 1;

    // Return new root
    return y;
}

### 2.3 AVL树的插入与删除算法
插入和删除节点时可能会破坏树的平衡性，需要进行相应的旋转操作以保持AVL树的平衡。

#### 2.3.1 插入操作引发的平衡调整
插入节点后，需要沿插入路径向上回溯，检查并修正每个节点的平衡因子，如果发现不平衡，执行相应的旋转操作。

// 插入后的平衡调整函数
struct AVLNode* rebalance(struct AVLNode* root) {
    int balanceFactor = getBalance(root);

    // Left Left Case
    if (balanceFactor > 1 && getBalance(root->left) >= 0)
        return rightRotate(root);

    // Left Right Case
    if (balanceFactor > 1 && getBalance(root->left) < 0) {
        root->left = leftRotate(root->left);
        return rightRotate(root);
    }

    // Right Right Case
    if (balanceFactor < -1 && getBalance(root->right) <= 0)
        return leftRotate(root);

    // Right Left Case
    if (balanceFactor < -1 && getBalance(root->right) > 0) {
        root->right = rightRotate(root->right);
        return leftRotate(root);
    }

    return root;
}

#### 2.3.2 删除操作引发的平衡调整
删除节点可能会导致子树高度变化，需要检查每个节点的平衡因子并可能执行旋转来恢复平衡。

### 2.4 AVL树的编程实践
在实际应用中，我们会定义AVL树的数据结构，并实现插入、删除、查找等操作。以下是一个简化的AVL树数据结构的实现。

#### 2.4.1 实现AVL树的数据结构

// AVL树节点结构体定义
struct AVLNode {
    int key;
    int height;
    struct AVLNode *left;
    struct AVLNode *right;
};

// 创建新节点的辅助函数
struct AVLNode* createNode(int key) {
    struct AVLNode* node = (struct AVLNode*)malloc(sizeof(struct AVLNode));
    node->key = key;
    node->height = 1; // 新节点被添加为叶子节点
    node->left = NULL;
    node->right = NULL;
    return(node);
}

#### 2.4.2 AVL树的应用示例
AVL树广泛应用于数据库索引、语言解析器的词法分析，以及任何需要维持有序且高度平衡的数据集合中。

// AVL树中插入节点的函数实现
struct AVLNode* insert(struct AVLNode* node, int key) {
    /* 1. 正常BST插入 */
    if