量子计算的桥梁：Kronecker积的应用理论与实践


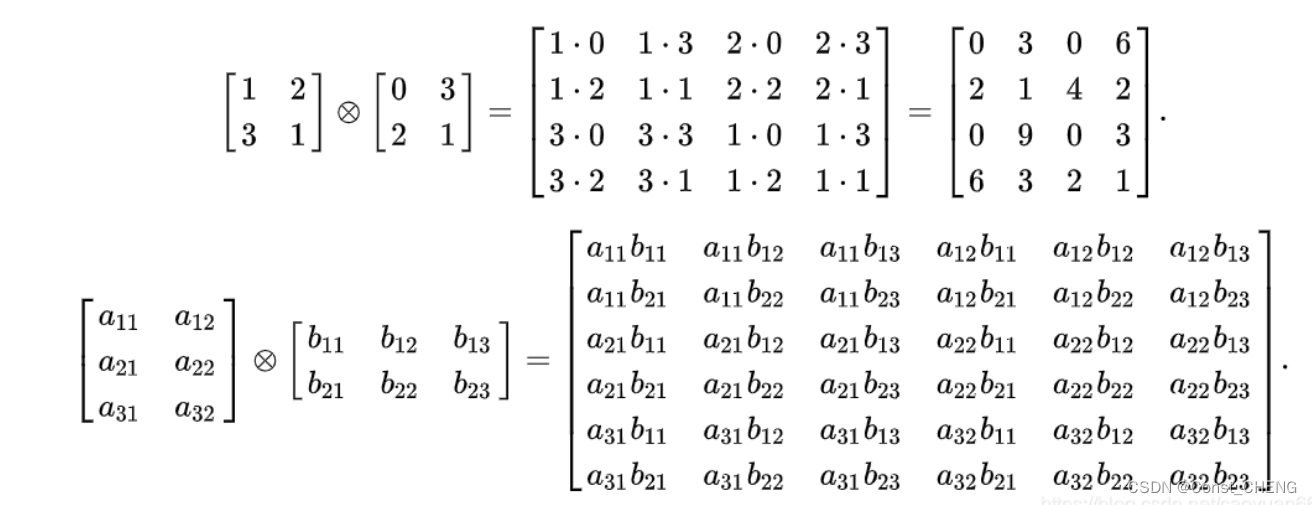
参考资源链接：[矩阵运算：Kronecker积的概念、性质与应用](https://wenku.csdn.net/doc/gja3cts6ed?spm=1055.2635.3001.10343)
# 1. 量子计算的基础概念和原理

量子计算是建立在量子力学基础之上的信息处理方法，它利用量子比特（qubits）来存储和处理信息，与传统计算的二进制位（bits）有着本质区别。量子比特可同时存在于多种状态中，这种现象称为量子叠加。此外，量子比特之间可以存在强关联，即量子纠缠，它赋予量子计算高度并行处理信息的能力。

量子计算的核心原理包括量子叠加、量子纠缠以及量子门操作。量子叠加允许量子比特在计算过程中同时考虑多种可能性，量子纠缠则允许量子比特之间分享信息，无论相隔多远。量子门操作通过精心设计的量子逻辑门来操作量子比特，执行各种计算任务。

本章将从量子力学的基本概念开始，详细阐述量子计算的工作原理和核心优势，为深入理解后续章节的Kronecker积在量子计算中的应用打下坚实基础。

# 2.2 Kronecker积在矩阵理论中的应用

### 2.2.1 线性代数中的作用

线性代数是处理向量空间及其变换的数学分支，在多个科学领域中都扮演着基础性角色。矩阵作为线性代数的一个核心元素，在描述线性变换和解决系统方程等方面具有不可替代的地位。而Kronecker积则是矩阵理论中的一个重要概念，它允许我们在更高维的框架内探讨线性变换的乘积。

当两个矩阵A和B进行Kronecker积运算后，生成一个新的矩阵，它描述了A和B所代表的线性变换同时作用于一个更广义的向量空间的情形。在实际应用中，比如在处理多个向量系统或者多维数据的线性变换时，Kronecker积提供了一种直观的工具。例如，在分析网络结构或者动态系统时，Kronecker积帮助我们将单个节点的特性推广到整个系统的框架中。

### 2.2.2 特殊矩阵的Kronecker积

特殊矩阵在数学中具有特定的性质和应用，如对角矩阵、单位矩阵、正定矩阵等。这些矩阵的Kronecker积通常会保留或产生一些有趣的性质，这些性质在理论和应用中都有重要的意义。

以单位矩阵为例，任何矩阵与单位矩阵的Kronecker积都保持原矩阵不变，这在简化复杂变换的表示中特别有用。在对角矩阵的情况下，两个对角矩阵的Kronecker积仍然是对角矩阵，且对角线上的元素为原来两个对角矩阵对角线上元素的乘积。这在处理具有特定结构的变换时提供了极大的便利。

这种特性也使得Kronecker积在特征值和特征向量问题中有特殊应用。例如，当需要计算两个矩阵乘积的特征值时，可以先计算这两个矩阵的Kronecker积，然后利用得到的更大矩阵的特征值来间接得到原始矩阵乘积的特征值，这在计算上有时会更加高效。

graph TD
    A[特殊矩阵] -->|单位矩阵| B[单位矩阵的Kronecker积]
    A -->|对角矩阵| C[对角矩阵的Kronecker积]
    A -->|正定矩阵| D[正定矩阵的Kronecker积]
    B --> E[保持原矩阵不变]
    C --> F[对角线元素乘积]
    D --> G[保持正定性]

请注意，表格、mermaid格式的流程图和代码块，在文章中应适当使用以提高内容的可读性和吸引力。在对代码块的使用中，每个代码块后面必须有逻辑分析和参数说明等扩展性说明。通过这种结构化和有序的展示方法，可以使读者更易理解复杂概念，并将理论知识应用于实际问题中。

# 3. Kronecker积的编程实现和案例分析

## 3.1 Kronecker积的计算方法
Kronecker积，也称为直积，是一种在数学领域中的二元运算，尤其在矩阵理论和量子计算中有着广泛的应用。本章节将深入探讨Kronecker积的计算方法，并从纯数学角度和量子计算平台两个维度进行分析。

### 3.1.1 纯数学方法的实现

纯数学方法实现Kronecker积涉及到矩阵运算，其核心思想是将两个矩阵A和B的每一个元素相乘后，根据矩阵A的行数和矩阵B的列数进行重新排列，形成一个新的矩阵。以下是一个简单的数学定义和直观理解：

假设有两个矩阵A(m x n)和B(p x q)，它们的Kronecker积，记作A ⊗ B，是一个大小为mp x nq的矩阵，通过以下方式构造：

A ⊗ B = [a11B  a12B  ...  a1nB]
        [a21B  a22B  ...  a2nB]
        [...    ...    ...   ...]
        [am1B  am2B  ...  amnB]

其中，aij是矩阵A中的元素，B是矩阵B。

为了编程实现这一过程，我们可以使用Python语言中的NumPy库，其提供了一个非常方便的方法`numpy.kron()`用于计算Kronecker积。

**代码示例：**

import numpy as np

# 定义矩阵A和B
A = np.array([[1, 2], [3, 4]])
B = np.array([[0, 5], [6, 7]])

# 计算Kronecker积
C = np.kron(A, B)

print("矩阵A:\n", A)
print("矩阵B:\n", B)
print("A ⊗ B:\n", C)

该代码将会输出两个输入矩阵和它们的Kronecker积。通过这个基础的编程实践，我们可以进一步探索Kronecker积在更复杂的数学运算和量子计算中的应用。

### 3.1.2 基于量子计算平台的实现

在量子计算平台中，Kronecker积不仅是一个数学上的概念，它还代表了量子比特和量子态的张量积。在量子计算中，Kronecker积能够用来表示更复杂的量子门操作，例如在构建量子电路时的复合门操作。

我们可以通过使用量子编程框架（如Qiskit、Cirq等）来实现量子计算平台上的Kronecker积。这些框架允许我们以图形化或脚本化的方式模拟量子电路的构建与执行。

**代码示例：**

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute, Aer

# 创建两个量子寄存器和经典寄存器
qreg1 = QuantumRegister(2, 'q1')
qreg2 = QuantumRegister(3, 'q2')
creg = ClassicalRegister(5, 'c')
circuit = QuantumCircuit(qreg1, qreg2, creg)

# 假设我们有两个量子操作U和V，现在我们使用Kronecker积来组合它们
# 这里我们使用简单的Pauli-X门作为示例
U = circuit.x(qreg1[0])
V = circuit.x(qreg2[1])

# 将U和V应用在由qreg1和qreg2组成的更大的量子系统上
circuit.compose([U, V], inplace=True)

# 运行电路
backend = Aer.get_backend('qasm_simulator')
result = execute(circuit, backend, shots=1).result()

# 输出结果
print(result.get_counts())

在这个示例中，我们构建了一个量子电路，包含了两个量子寄存器和一个经典寄存器。我们定义了两个量子操作，并使用`compose`方法将它们组合。这种组合本质上是通过Kron