【数字信号处理快速上手】:第4版第10章习题,权威指南与学习心得
发布时间: 2024-12-16 02:54:25 阅读量: 1 订阅数: 2 


MATLAB在信号处理中的应用:基础与高级技术详解
参考资源链接:[数字信号处理 第四版 第10章习题答案](https://wenku.csdn.net/doc/6qhimfokjs?spm=1055.2635.3001.10343)
# 1. 数字信号处理基础理论
数字信号处理(DSP)是现代通信、控制和信息处理技术的核心部分,它涉及从原始信号中提取信息,以及改善信号质量以实现特定的应用需求。在深入理解复杂的数字信号处理技术之前,有必要掌握一些基础理论。
## 1.1 信号的定义与分类
信号可以定义为携带信息的物理量,它们可以是时间的函数,也可以是空间的函数。根据信号的形式和性质,我们可以将其分为连续时间信号和离散时间信号。
**连续时间信号**在时间和幅度上都是连续的,常见的例子包括模拟音频信号。而**离散时间信号**在时间和幅度上是离散的,常用于数字信号处理,如计算机中处理的音频文件。
## 1.2 信号的基本属性
信号具有多个基本属性,这些属性对于理解信号处理是至关重要的:
- **幅度**:信号的强度或大小。
- **频率**:单位时间内周期性变化的次数。
- **相位**:信号周期变化的起始位置。
掌握这些基本属性,是进行有效信号处理分析的前提条件。接下来的章节,我们将探讨信号的时域和频域表示方法,以及如何在实际应用中实现和优化这些技术。
# 2. 信号的时域分析与实现
### 2.1 时域信号的表示方法
#### 2.1.1 连续时间信号与离散时间信号
在数字信号处理(DSP)的背景下,时域分析的第一步是对信号的表示进行区分。连续时间信号是连续变化的,其值可以在任意时间点被定义。这种信号通常是模拟信号,可以通过电子设备(如麦克风、传感器)直接捕捉到。然而,为了在数字系统中处理信号,我们必须将连续时间信号转换为离散时间信号。离散时间信号由一系列离散的样本点组成,这些样本点是在特定的时间间隔内对连续时间信号进行采样的结果。
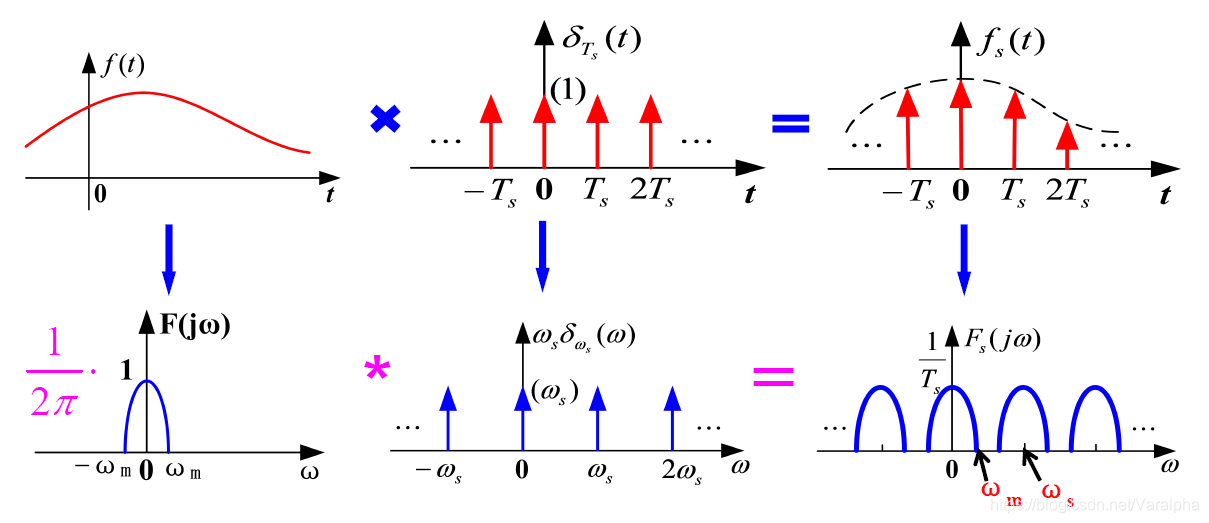
这种从连续到离散的转换过程被称为采样。根据奈奎斯特采样定理,为了准确重构原始的连续时间信号,采样频率必须至少是信号最高频率成分的两倍。采样过程可以通过一个理想化的模型表示,其中连续信号与一个冲激序列相乘,产生离散信号。
```matlab
% 一个简单的示例代码来演示连续信号到离散信号的转换
% 定义连续时间信号
t = 0:0.001:1; % 时间向量从0到1秒,步长为0.001秒
x_cont = sin(2*pi*10*t); % 一个频率为10Hz的正弦信号
% 采样连续信号得到离散信号
Fs = 1000; % 采样频率为1000Hz
x_disc = sin(2*pi*10*(0:1/Fs:1)); % 以1000Hz的频率采样10Hz的正弦信号
% 绘制连续信号和离散信号
figure;
subplot(2,1,1);
plot(t, x_cont);
title('连续时间信号');
xlabel('时间 (秒)');
ylabel('幅度');
subplot(2,1,2);
stem(0:1/Fs:1, x_disc, 'filled');
title('离散时间信号');
xlabel('时间 (秒)');
ylabel('幅度');
```
在上述MATLAB代码中,我们首先定义了一个10Hz的正弦波形连续信号,并以1000Hz的采样频率对其进行采样,得到离散信号。然后,我们使用`plot`函数绘制连续信号的图形,并使用`stem`函数显示离散信号的样本点。
#### 2.1.2 常用时域分析方法概述
时域分析是数字信号处理中最直观的方法之一,它包括对信号波形的直接观察,以及对信号特性的定量测量。常见的时域分析方法包括:
- **波形观察:** 通过绘制信号的图形来直观地观察其特征,如幅度、周期、趋势等。
- **统计测量:** 计算信号的均值、方差、标准差等统计量,以表征信号的统计特性。
- **信号相关性:** 分析两个信号之间的相似性或因果关系,常用于信号同步和去噪。
- **自相关和互相关:** 自相关用于分析信号的周期性,而互相关用于检测两个信号之间的相似性。
在实际应用中,这些方法往往需要结合使用,以获得更全面的信号特性分析。例如,工程师可能首先通过波形观察获取信号的直观信息,然后使用统计测量来了解信号的总体行为,最后利用信号相关性来研究信号之间的动态关系。
### 2.2 时域信号的处理技术
#### 2.2.1 卷积和相关操作
卷积和相关是信号处理中非常重要的操作,它们在分析线性时不变系统(LTI系统)中起着核心作用。卷积可以被看作是对系统输入信号和系统冲激响应之间的一种“加权叠加”操作,它描述了当输入信号通过LTI系统时的输出信号。
- **卷积的数学定义:** 对于两个信号\(x[n]\)和\(h[n]\),它们的卷积定义为:
\[
y[n] = (x * h)[n] = \sum_{k=-\infty}^{\infty} x[k]h[n-k]
\]
在实际计算过程中,由于计算机处理的是有限长度的离散信号,所以通常使用有限卷积(卷积和)的概念。
- **相关操作:** 相关操作与卷积相似,但它不涉及信号的反转。相关可以用于测量两个信号之间的相似性,其数学表达式为:
\[
y[n] = (x \star h)[n] = \sum_{k=-\infty}^{\infty} x[k]h[n+k]
\]
以下是实现这两个操作的Python代码片段,使用了NumPy库:
```python
import numpy as np
# 示例信号定义
x = np.array([1, 2, 3])
h = np.array([2, 3, 4])
# 卷积操作
conv_result = np.convolve(x, h, mode='full')
# 相关操作
corr_result = np.correlate(x, h, mode='full')
print("卷积结果:", conv_result)
print("相关结果:", corr_result)
```
#### 2.2.2 信号的时移、时域反转和尺度变化
信号的时移、时域反转和尺度变化是调整信号时域表示的基本手段。这些操作在信号预处理和系统分析中非常有用。
- **时移:** 将信号沿时间轴进行移动。时移操作不会改变信号的形状,只是改变了信号出现的时间。
- **时域反转:** 将信号关于时间轴进行翻转。对于离散信号而言,时域反转后,信号的时间索引也将反转。
- **尺度变化:** 改变信号时间轴的单位,可以对信号进行压缩或扩张,而不改变信号的形状。
这些操作可以通过简单的数学变换来实现。以下为Python代码示例:
```python
# 定义信号
x = np.array([1, 2, 3, 4])
# 时移操作
shifted_x = np.roll(x, 2) # 向右移动2个位置
# 时域反转操作
reversed_x = x[::-1] # 反转信号
# 尺度变化操作(扩张)
dilated_x = np.repeat(x, 2) # 将每个元素重复2次
print("时移后的信号:", shifted_x)
print("时域反转后的信号:", reversed_x)
print("尺度变化后的信号(扩张):", dilated_x)
```
### 2.3 习题解析:时域分析技术的应用
#### 2.3.1 典型题目解析
在学习时域分析技术时,解决典型题目是加深理解的重要环节。例如,考虑一个离散时间信号\(x[n]\),并使用卷积操作来模拟一个简单的LTI系统响应。
假设我们有输入信号\(x[n] = \delta[n] + 2\delta[n-1]\),其中\(\delta[n]\)是单位冲激函数,和系统冲激响应\(h[n] = \delta[n] - \delta[n-1]\),求系统输出\(y[n]\)。
根据卷积的定义,我们可以计算得到:
\[
\begin{align*}
y[0] &= (x * h)[0] = 1 \cdot 1 + 0 \cdot (-1) = 1 \\
y[1] &= (x * h)[1] = 1 \cdot (-1) + 2 \cdot 1 = 1 \\
y[n] &= 0 \text{ for } n > 1
\end{align*}
\]
因此,系统输出为\(y[n] = \delta[n] + \delta[n-1]\)。
通过这种方式,我们可以深入理解卷积在信号处理中的作用和意义。
#### 2.3.2 解题思路和技巧分享
在解题时,有几个技巧可以帮助简化问题:
1. **画图法:** 在纸上画出信号的波形图,帮助直观理解信号的时间关系。
2. **对称性分析:** 利用信号的对称性(如实数信号的对称性)来简化计算。
3. **边界处理:** 理解卷积中的边界效应,并知道如何处理它们,特别是在有限序列的情况下。
4. **利用卷积性质:** 使用卷积的性质,如交换律、结合律和分配律,来简化问题。
5. **软件工具:** 使用诸如MATLAB或Python这样的软件工具进行数值计算和图形显示。
通过这些策略,处理时域分析的习题变得更加高效和有条理。
以上为第二章的内容概述。每一部分的展开都需要细致的逻辑分析和示例来阐明,确保内容的丰富性和深度。
# 3. 信号的频域分析与实践
## 3.1 频域分析基础
### 3.1.1 傅里叶变换的基本概念
傅里叶变
0
0






