【ROC曲线全面解析】：从基础到实战，掌握模型评估的黄金标准

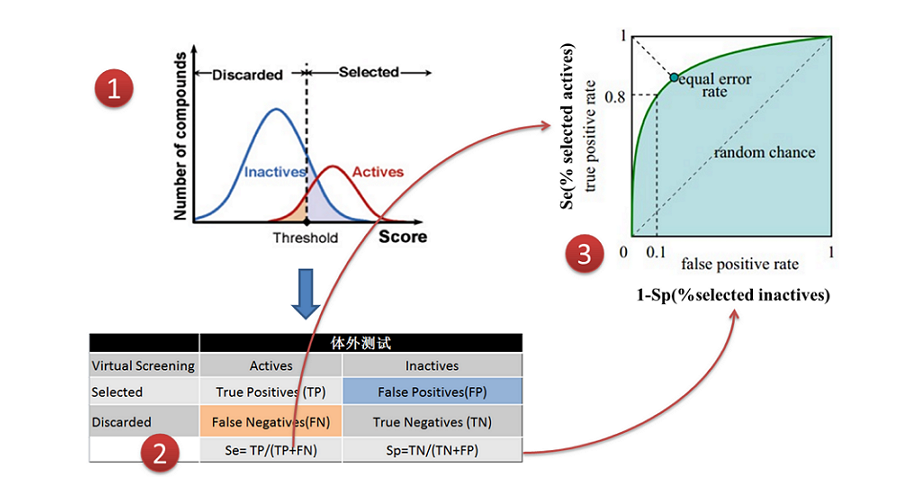
# 1. ROC曲线的基本概念与重要性

ROC曲线是模型性能评估中的一种常用工具，它通过图示的方式呈现了分类器在不同阈值下的真正类率(True Positive Rate, TPR)与假正类率(False Positive Rate, FPR)之间的关系。理解ROC曲线对于评估和比较机器学习模型在二分类问题中的性能至关重要。本章节将介绍ROC曲线的基本概念，并阐释其在模型评估中的重要性。

ROC曲线的优势在于它不受类不平衡的影响，并且能通过曲线下面积(Area Under the Curve, AUC)来提供一个单一的性能指标。这种特性使得ROC曲线成为衡量分类器总体性能的有力工具。在接下来的章节中，我们将深入探讨ROC曲线的理论基础和实际应用，帮助读者全面掌握这一核心概念。

# 2. ROC曲线的理论基础

## 2.1 二分类问题与混淆矩阵

### 2.1.1 理解二分类问题

在机器学习中，二分类问题是将实例数据分配到两个类别中的一个，常见于诸如疾病检测、垃圾邮件识别等多种场景。例如，在疾病检测中，模型需要判断患者是否患病，即输出为“患病”或“未患病”的二元判定。

为了理解二分类问题，需要明确几个关键概念：
- **真正类（True Positive, TP）**：模型正确地将正类判定为正类。
- **假负类（False Negative, FN）**：模型错误地将正类判定为负类。
- **假正类（False Positive, FP）**：模型错误地将负类判定为正类。
- **真负类（True Negative, TN）**：模型正确地将负类判定为负类。

二分类问题的评估涉及到判断模型对这些类别的区分能力，而混淆矩阵是评估这种能力的重要工具。

### 2.1.2 混淆矩阵的构建与解读

混淆矩阵是一种特殊的表格布局，用来可视化算法性能，尤其是分类问题。它由以下四个部分组成：

| 真实\预测 | 预测正类 | 预测负类 |
|-----------|------------|------------|
| 实际正类 | 真正类（TP）| 假负类（FN）|
| 实际负类 | 假正类（FP）| 真负类（TN）|

具体解读如下：
- **真正类率（TPR）**：TP / (TP + FN)，又称“灵敏度”，表示模型识别正类的能力。
- **假正类率（FPR）**：FP / (FP + TN)，表示模型错误识别为正类的负类比例。
- **精确率（Precision）**：TP / (TP + FP)，表示模型输出为正类的结果中，实际为正类的比例。
- **负类精确率（Neg. Prec.）**：TN / (TN + FN)，表示模型输出为负类的结果中，实际为负类的比例。

通过构建混淆矩阵，我们可以更深入地了解模型在各个分类上的表现，为后续的ROC曲线分析奠定基础。

## 2.2 ROC曲线的数学原理

### 2.2.1 真正例率（TPR）与假正例率（FPR）

真正例率（True Positive Rate, TPR）和假正例率（False Positive Rate, FPR）是ROC曲线分析中的两个核心概念，它们的计算方式如下：

- **TPR** = 真正类数 / (真正类数 + 假负类数) = TP / (TP + FN)
- **FPR** = 假正类数 / (假正类数 + 真负类数) = FP / (FP + TN)

它们是针对不同的阈值设定的性能度量指标。在二分类问题中，通过调整阈值（比如概率阈值），我们可以改变TPR和FPR，从而得到一系列的点。这些点构成了ROC曲线。

### 2.2.2 ROC空间与曲线绘制

ROC空间是TPR与FPR的坐标系图，横轴为FPR，纵轴为TPR。在ROC空间中，当模型随机猜测时，TPR和FPR相等，对应的是斜率为1的直线，这被称为“随机线”。

ROC曲线的绘制步骤如下：
1. 对模型的预测结果按概率从高到低排序。
2. 设置一系列的阈值（从1开始到0），每个阈值对应一个TPR和FPR。
3. 在ROC空间中绘制这些点，并连接它们。

理想模型的ROC曲线会向左上角弯曲，远离随机线。而在实际应用中，根据模型的性能，ROC曲线可能在随机线之上或之下。ROC曲线越接近左上角，表明模型的区分能力越强。

## 2.3 ROC曲线与模型性能评估

### 2.3.1 AUC值的含义及其计算

**AUC**（Area Under the Curve）值是指ROC曲线下的面积，用来量化模型性能。AUC值的范围在0到1之间，一个完美的分类器，其AUC值为1，而随机猜测模型的AUC值为0.5。

AUC值可以通过积分或近似方法来计算。在实际应用中，通常使用梯形规则来近似计算AUC值。具体操作是将ROC曲线下的面积分割成若干小梯形，然后计算这些梯形的面积和。

### 2.3.2 ROC曲线下的面积（AUC）的意义

AUC值是一个非常有用的度量，因为它综合考虑了模型对正负类的区分能力。一个高AUC值的模型表明，它不仅能够将正类和负类区分开，而且具有较好的泛化能力。

AUC值对于不平衡的数据集特别有用，因为它不依赖于类别的分布，能够避免由于类别不平衡导致的评估偏差。此外，AUC值是一个单一的数值指标，容易比较不同模型的性能。

此外，AUC值也可以用来评估模型预测概率的排序能力。在许多实际问题中，特别是需要排序的场景，如信用评分和风险评估，AUC值提供了对模型性能的直观评估。

在下一章节中，我们将详细介绍ROC曲线在实际应用中的使用方法，包括如何通过ROC曲线选择最佳阈值以及不同模型间的ROC曲线比较。

# 3. ROC曲线的实战应用

ROC曲线不仅是理论上的概念，在实际的数据分析和模型评估中，它也扮演着至关重要的角色。本章节将深入探讨ROC曲线在实际问题解决中的应用，包括如何使用ROC曲线进行模型比较，ROC曲线在特定领域的应用场景，以及它与其它评价指标如何结合使用。

## 使用ROC曲线进行模型比较

ROC曲线被广泛用于模型比较，因为它提供了一个单一的性能指标（AUC值），能够帮助我们快速识别出最佳的分类模型。

### 选择最佳阈值

在使用ROC曲线进行模型比较之前，首先需要明确如何选择最佳阈值。阈值的选择对于二分类问题的预测结果至关重要，因为它决定了正负类别的判定边界。

**代码逻辑与分析：**

from sklearn.metrics import roc_curve, auc

# 假设fpr, tpr, thresholds为通过模型计算得到的ROC曲线上的点及其对应的阈值
fpr, tpr, thresholds = roc_curve(y_true, y_scores)

# 计算AUC值
roc_auc = auc(fpr, tpr)

# 打印阈值与对应的真正例率（TPR）
for threshold, tpr in zip(thresholds, tpr):
    print(f"阈值: {threshold:.4f}, TPR: {tpr:.4f}")

在这段代码中，我们首先计算了ROC曲线上的点及其对应的阈值，并使用`auc`函数计算了曲线下的面积（AUC值）。然后，我们遍历所有阈值与对应的TPR值，以找到最适合业务需求的阈值。

### 不同模型的ROC曲线比较

通过比较不同模型的ROC曲线，我们可以直观地了解哪个模型在分类任务中表现最佳。

**图表展示：**

这里可以使用一个图表来直观展示不同模型的ROC曲线对比。

graph LR
A[模型A的ROC曲线] -->|比较| B[模型B的ROC曲线]
B -->|对比| C[模型C的ROC曲线]
C -->|综合评估| D[最佳模型选择]

在实际操作中，我们会生成多个模型的ROC曲线，然后对比它们在ROC空间中的表现。模型的AUC值越大，表明其曲线越接近左上角，因此性能越好。

## ROC曲线在不同场景的应用

ROC曲线不仅适用于一般性的模型比较，它还被应用到了多个特定的业务场景中，为不同领域的问题解决提供了独特的视角。

### 金融风控领域的应用实例

在金融风控领域，ROC曲线被用来评估信用评分模型的分类性能。

**逻辑分析：**

# 金融风控模型的ROC曲线计算
fpr_financial, tpr_financial, _ = roc_curve(y_true_financial, y_scores_financial)

# 绘制金融风控模型的ROC曲线
plt.plot(fpr_financial, tpr_financial, label='Financial ROC Curve (AUC = %0.2f)' % roc_auc_financial)
plt.plot([0, 1], [0, 1], 'k--')  # 随机猜测的参考线
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.title('ROC Curve for Financial Credit Scoring')
plt.legend(loc="lower right")
plt.show()

在此代码块中，我们绘制了金融风控模型的ROC曲线，并添加了一条随机猜测的参考线，以便更直观地评价模型性能。

### 医疗诊断领域的应用实例

在医疗诊断中，ROC曲线同样重要。它能够帮助医生和医疗研究人员选择出最适合的诊断模型。

**表格展示：**

| 模型名称 | 真阳性率 (TPR) | 假阳性率 (FPR) | AUC值 | 特定条件下的表现 |
| --------- | -------------- | -------------- | ----- | ---------------- |
| 模型X | 0.90 | 0.10 | 0.93 | 在高危人群中表现良好 |
| 模型Y | 0.85 | 0.08 | 0.89 | 对老年人群准确率高 |
| 模型Z | 0.95 | 0.15 | 0.90 | 在早期诊断方面出色 |

该表格展示了三种医疗诊断模型在特定条件下的性能评估。

## ROC曲线与其它评价指标的结合

单一的评价指标很难全面地描述一个模型的性能。因此，将ROC曲线与其他评价指标结合使用，可以从不同角度全面评价模型的优劣。

### ROC与精确率-召回率曲线（PR曲线）

ROC曲线和精确率-召回率（Precision-Recall, PR）曲线常常一起使用，它们在不同的数据集上提供了不同的洞见。

**代码实现：**

from sklearn.metrics import precision_recall_curve

# 假设precision, recall, thresholds为计算得到的PR曲线上的点及其对应的阈值
precision, recall, _ = precision_recall_curve(y_true, y_scores)

# 绘制PR曲线
plt.plot(recall, precision, label='Precision-Recall Curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.legend(loc="lower left")
plt.show()

在这个例子中，我们绘制了PR曲线，并可以与ROC曲线进行对比，以评价模型在不同方面的性能。

### 结合成本敏感度的评价指标

在实际应用中，不同类型的错误往往带有不同的成本。结合成本敏感度的评价指标可以帮助我们更深入地了解模型在实际应用中的效果。

**参数说明：**
- `cost_matrix`：成本矩阵，用于定义不同错误类型的成本。
- `thresholds`：模型输出的阈值。

**代码逻辑：**

# 假设的错误成本
cost_matrix = np.array([[0, 1], [5, 0]])

# 根据不同的阈值计算成本
for threshold in thresholds:
    # 模型预测结果
    y_pred = np.where(y_scores > threshold, 1, 0)
    # 计算每个样本的错误成本
    errors_cost = np.sum(cost_matrix[y_pred != y_true])
    print(f"阈值: {threshold:.4f}, 错误成本: {errors_cost:.2f}")

通过上面的代码，我们能够计算出在不同阈值下模型的错误成本，进而选择一个具有最小成本的阈值，以优化实际应用中的模型性能。

# 4. ROC曲线的高级应用

## 4.1 ROC曲线在多分类问题中的应用
### 4.1.1 多分类问题的ROC曲线

在多分类问题中，ROC曲线的使用并不像二分类问题那样直接。每个类别都需要一个ROC曲线，因此我们可能面临多个ROC曲线，这些曲线可以提供关于模型在不同类别的表现信息。多分类问题中的ROC曲线通常会采用一个称为“一对多”（One-vs-All）或“一对一”（One-vs-One）的策略。

在“一对一”策略中，对于K个类别的问题，我们需要构造K(K-1)/2个分类器，每个分类器将一个类别与其他所有类别分开。这会产生K(K-1)/2个ROC曲线，对于每个类别分别表示其在与所有其他类别区分时的性能。

在“一对多”策略中，对于每个类别，我们构建一个将该类别与所有其他类别分开的分类器。这会产生K个ROC曲线，每个曲线对应一个类别在与所有其他类别区分时的性能。

### 4.1.2 一对一与一对多的ROC分析方法

选择“一对一”还是“一对多”策略取决于具体问题的需求。在类别不平衡的数据集中，“一对一”方法可能会导致对少数类的过拟合，因为分类器需要在一个类别与一个非常大的“其他”类别之间进行区分。相反，“一对多”方法可能在类别较多的情况下计算成本较高，但它通常更适合处理类别不平衡问题，因为它比较的是一个类别与一个明确的集合。

在实际应用中，我们可以利用绘制多ROC曲线的方法来评估模型的泛化能力。通过观察曲线的形状和分布，我们可以获得有关模型在不同类别间区分能力的信息。例如，如果一个类别对应的ROC曲线明显比其他类别的曲线更差，这可能表明该类别较难被模型准确预测。

## 4.2 ROC曲线的定制化与优化
### 4.2.1 特定需求下的ROC曲线调整

在某些特定的应用中，标准的ROC曲线可能无法完全满足需求。例如，对于某些实时决策系统，可能需要一个优化的阈值，使得模型在特定条件下的性能最优化，比如减少假阴性或假阳性。在这种情况下，ROC曲线可以用来帮助定制化调整以满足特定的业务需求。

为了调整ROC曲线，我们可以通过改变分类阈值来查看不同点对应的TPR和FPR。在图表中，这些点将沿着ROC曲线移动。选择一个合适的阈值，我们可以在保持较高TPR的同时最小化FPR，或者根据实际需要在其他方面进行权衡。

### 4.2.2 ROC曲线的统计显著性测试

在统计学中，我们通常会进行显著性测试以确定结果是否具有统计学意义。在使用ROC曲线时，我们也可以对模型的性能进行显著性测试，以判断不同模型间的性能差异是否具有统计学意义，或者不同分类阈值的选择是否显著地影响了模型性能。

一种方法是对不同模型的AUC值进行比较。如果两个模型的AUC值差异显著，这可能表明一个模型在整体上比另一个模型表现更好。然而，AUC值只能告诉我们模型的总体性能，并不能给出性能差异在何处发生。因此，我们还需要进行更细致的分析，比如对特定的FPR区间进行比较，或者通过具体点的TPR和FPR差异来分析。

## 4.3 ROC曲线与机器学习的结合
### 4.3.1 ROC曲线在集成学习中的应用

集成学习是机器学习中一种重要的方法，它通过结合多个模型的预测来提高整体性能。ROC曲线在评估集成学习模型时同样适用，并且能够提供关于集成模型在不同分类阈值下的性能表现。

在集成学习中，如随机森林或梯度提升树等模型，通常会有一个超参数用来控制模型的复杂度或正则化。通过改变这些超参数，我们可以生成一系列不同的模型，进而绘制出一条包含所有模型性能的ROC曲线。这种方法可以帮助我们找到最优的超参数设置。

### 4.3.2 ROC优化的机器学习算法案例研究

为了深入探讨ROC曲线在机器学习中的应用，我们可以通过一个实际的案例研究。例如，考虑一个信用卡欺诈检测的问题，在这个问题中，我们希望建立一个高精度的模型来检测欺诈交易。我们可以使用不同的机器学习算法，比如逻辑回归、支持向量机（SVM）或神经网络，并对每个模型绘制ROC曲线。

在每个模型的ROC曲线基础上，我们可以优化模型的分类阈值。这通常涉及到对模型的预测输出进行重新校准，以提高其在某些重要性能指标上的表现。例如，考虑到银行可能更关心降低误报率以减少调查成本，我们可以选择一个在FPR较低区域表现出色的模型，即使这可能会导致TPR略有下降。

让我们以逻辑回归模型为例，探索如何优化和解读ROC曲线。首先，我们拟合一个逻辑回归模型，并得到概率预测。然后，我们可以设置不同的阈值，比如从0.1到0.9，每间隔0.05，并计算每个阈值对应的TPR和FPR，绘制出ROC曲线。

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt

# 假设X_train是训练特征，y_train是训练标签
model = LogisticRegression()
model.fit(X_train, y_train)

# 预测概率
y_scores = model.predict_proba(X_test)[:, 1]

# 计算ROC曲线
fpr, tpr, thresholds = roc_curve(y_test, y_scores)

# 计算AUC值
roc_auc = auc(fpr, tpr)

# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()

通过上述Python代码，我们拟合了逻辑回归模型，并绘制了ROC曲线。我们可以通过调整`predict_proba`中的阈值参数来观察不同阈值下的性能。此案例展示了ROC曲线在机器学习模型性能评估中的实际应用，以及如何通过ROC曲线进行模型优化。通过不断调整和重新评估，我们可以找到最适合我们问题的模型配置。

# 5. ROC曲线工具与资源

在机器学习和数据科学领域，评估模型性能是一个至关重要的步骤。ROC曲线作为识别模型分类性能的强大工具，已经广泛应用于各种分析中。但如何有效地使用ROC曲线，以及如何选择合适的工具来实现这一目的，是每个数据科学家和机器学习工程师都需要掌握的技能。本章节将深入探讨ROC曲线相关的工具和资源，并介绍如何通过编程语言实现ROC分析，以及如何自定义一个ROC分析工具。

## 5.1 常用的ROC分析工具介绍

ROC曲线的分析和绘制可以通过多种方式实现，既可以使用现成的软件工具和库，也可以利用在线平台。接下来将详细介绍这些工具，并比较它们的优缺点。

### 5.1.1 软件工具和库的比较

在数据科学中，有一些专门用于绘制ROC曲线的软件工具和编程库，它们各有特色，适用于不同的需求。

#### **MATLAB**

MATLAB是一个高性能的数值计算环境和第四代编程语言，它提供了强大的ROC分析功能。通过内置的`perfcurve`函数，用户可以方便地生成ROC曲线。此外，MATLAB的GUI工具箱（如Bioinformatics Toolbox）为绘制ROC曲线提供了可视化界面。

- **优点**: 用户界面友好，功能强大，适合于研究和教学环境。
- **缺点**: 商业软件，对于个人用户可能较为昂贵。

#### **Python - scikit-learn**

Python是一个开源的编程语言，广泛应用于科学计算和数据分析，而scikit-learn库是Python中用于机器学习的一个最重要的库之一。它提供了`roc_curve`函数和`roc_auc_score`来绘制ROC曲线并计算AUC值。

- **优点**: 开源，免费，拥有庞大的社区支持，提供了丰富的方法和函数。
- **缺点**: 初学者可能需要一定的时间来熟悉其API和函数。

#### **R语言 - pROC包**

R语言是一种专门用于统计分析的语言，而pROC包是R中最流行的ROC分析工具之一。它允许用户绘制ROC曲线，并执行各种统计测试来比较不同的ROC曲线。

- **优点**: 针对统计分析优化，拥有许多专门的统计功能。
- **缺点**: 对于非统计专业的用户来说，可能需要更多的学习成本。

### 5.1.2 在线ROC分析平台

除了传统的软件和编程库之外，还有一些在线平台可以提供ROC曲线的分析和绘制服务。这些工具通常具有易用性高，无需安装的特点。

#### **Plotly**

Plotly是一个用于创建交互式图表的在线平台。用户可以将数据上传至Plotly，使用它的ROC曲线模板轻松创建图表。Plotly支持将图表嵌入到网页中，也可以导出为多种格式。

- **优点**: 无需编码，图形美观，易于分享和展示。
- **缺点**: 交互式图表可能导致加载速度慢，且对数据隐私有一定风险。

## 5.2 开发者如何实现ROC曲线分析

为了深入理解ROC曲线分析的实现细节，开发者需要亲自编写代码来完成这一过程。以下将通过编程语言中的ROC分析实现，以及自定义ROC分析工具的实战案例，带领读者了解这个过程。

### 5.2.1 编程语言中的ROC分析实现

#### Python中使用scikit-learn绘制ROC曲线

from sklearn.metrics import roc_curve, auc
from sklearn import datasets
import matplotlib.pyplot as plt

# 加载数据集
data = datasets.load_breast_cancer()
X = data.data
y = data.target

# 假设我们已经有一个训练好的逻辑回归模型：model
# model.predict_proba(X_test) 返回预测的概率值

# 计算ROC曲线和AUC值
fpr, tpr, thresholds = roc_curve(y, model.predict_proba(X)[:, 1])
roc_auc = auc(fpr, tpr)

# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()

- **参数解释**: `roc_curve`函数接收真实标签和预测概率，输出假正例率(FPR)、真正例率(TPR)和阈值。`auc`函数计算ROC曲线下的面积。
- **代码逻辑分析**: 代码首先导入必要的库和函数，然后加载数据集。通过模型的`predict_proba`方法获得预测概率，并与实际标签结合调用`roc_curve`函数。最后绘制ROC曲线并展示。

### 5.2.2 实战：自定义ROC分析工具

现在，让我们通过一个实际案例来学习如何从零开始构建一个简单的ROC分析工具。

#### 实现步骤

1. **初始化参数**: 设置阈值的起始和终止范围。
2. **生成ROC数据**: 对于每个阈值，计算出对应的TPR和FPR。
3. **绘制ROC曲线**: 使用生成的TPR和FPR数据来绘制曲线。
4. **计算AUC值**: 通过梯形法则计算曲线下面积。

#### 示例代码

import numpy as np
import matplotlib.pyplot as plt

# 示例数据
y_true = np.array([1, 1, 1, 0, 0, 1])
y_scores = np.array([0.9, 0.8, 0.35, 0.6, 0.2, 0.7])

# 初始化TPR和FPR列表
fpr, tpr, thresholds = [], [], []

# 计算TPR和FPR
for t in np.unique(y_scores):
    tp = np.sum((y_scores >= t) & (y_true == 1))
    fp = np.sum((y_scores >= t) & (y_true == 0))
    fn = np.sum((y_scores < t) & (y_true == 1))
    tn = np.sum((y_scores < t) & (y_true == 0))
    tpr.append(tp / (tp + fn))
    fpr.append(fp / (fp + tn))
    thresholds.append(t)

# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr)
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.show()

# 计算AUC值
auc_score = sum([((fpr[i] - fpr[i-1]) * (tpr[i-1] + tpr[i])) / 2 for i in range(1, len(fpr))])
print(f"Calculated AUC score: {auc_score}")

- **代码逻辑分析**: 示例代码首先初始化真实标签和预测分数，然后通过迭代不同的阈值来计算TPR和FPR，绘制ROC曲线，并计算AUC值。这里使用了简化的梯形法则来进行AUC的近似计算。
- **逻辑扩展**: 在真实应用场景中，数据集可能更为复杂，可能包含多个类别，因此代码需要根据实际情况进行相应的调整和优化。

本章节内容涵盖了ROC曲线分析工具和资源，不仅提供了现成工具的比较和选择指南，还详细说明了如何通过编程语言实现ROC曲线分析，最后通过实战案例进一步加深了对ROC曲线分析的理解。这些知识和技能对于数据科学家和机器学习工程师来说是必不可少的，它们将帮助他们更好地评估和优化机器学习模型。

# 6. 总结与未来展望

## 6.1 ROC曲线的局限性与挑战

ROC曲线虽然在模型评估领域被广泛应用，但它也存在一定的局限性。了解这些局限性对于正确解读ROC曲线以及未来的发展研究非常重要。

### 6.1.1 现有局限性的讨论

首先，ROC曲线在处理不平衡数据集时可能会产生误导性的结果。在某些情况下，正负样本比例严重不均，即使模型表现不佳，ROC曲线也可能显示较好的性能。为解决这一问题，研究者提出了一种调整方法，即使用加权ROC曲线，其中不同的TPR和FPR具有不同的权重，从而更公正地反映模型性能。

其次，ROC曲线不考虑类别预测的绝对概率值，仅关注排名。这意味着即使两个模型在ROC曲线上表现相似，它们的预测概率也可能大相径庭。PR曲线在这方面提供了更多信息，它考虑了正类的精确度，因此在某些情况下，特别是正例十分罕见时，PR曲线可能更加适合。

### 6.1.2 面临的新问题与挑战

随着机器学习模型变得越来越复杂，评估模型的难度也相应增加。例如，深度学习模型通常有数以百万计的参数，评估这些模型在不同分布下的表现变得异常困难。因此，开发能够处理大规模数据和复杂模型的ROC曲线变体，将是未来的一个研究方向。

此外，多标签分类问题为ROC曲线的使用带来了新的挑战。在多标签分类中，一个实例可能属于多个类别，传统的ROC曲线可能不足以全面评估模型性能。研究者需要开发新的评价方法，以更全面地衡量多标签分类模型的性能。

## 6.2 未来发展趋势与研究方向

### 6.2.1 ROC曲线的发展趋势

随着数据分析技术的进步，ROC曲线分析工具将变得更加高效和用户友好。我们可以预见，未来将有更多的自动化和智能化工具出现，这些工具不仅能够帮助用户绘制ROC曲线，还能提供模型性能的深入分析，并给出优化建议。

此外，随着解释性AI的发展，ROC曲线也将变得更加可解释。研究者正在寻找方法，使得机器学习模型的结果不仅准确，而且易于理解。解释性ROC曲线将有助于用户了解模型为何给出特定的评估结果，从而促进模型的透明性和信任度。

### 6.2.2 模型评估领域的新兴方法探索

未来，我们可能会看到更多基于ROC曲线的评价指标和优化方法。例如，集成学习方法可能会与ROC曲线结合，以提高模型的泛化能力。研究人员也可能寻找将ROC曲线与其他评估指标结合的新方式，比如与F1分数、Brier得分或其他度量标准的结合使用。

随着人工智能在各个行业的深入应用，评估方法将需要适应更加具体和动态变化的需求。例如，医疗健康领域需要高度敏感且特异性的模型，这可能会推动评估指标向更细致的方向发展，以便更精确地量化模型性能。

在这个章节中，我们探讨了ROC曲线在实际应用中可能面临的局限性，并对未来的趋势进行了展望。尽管ROC曲线不是完美的工具，但它仍然是模型性能评估中不可或缺的一部分。随着新问题的出现和新技术的发展，ROC曲线可能会被进一步改进，以更好地适应不断变化的需求。