【组合数据结构的艺术】：揭秘组合数据结构的优势与应用场景

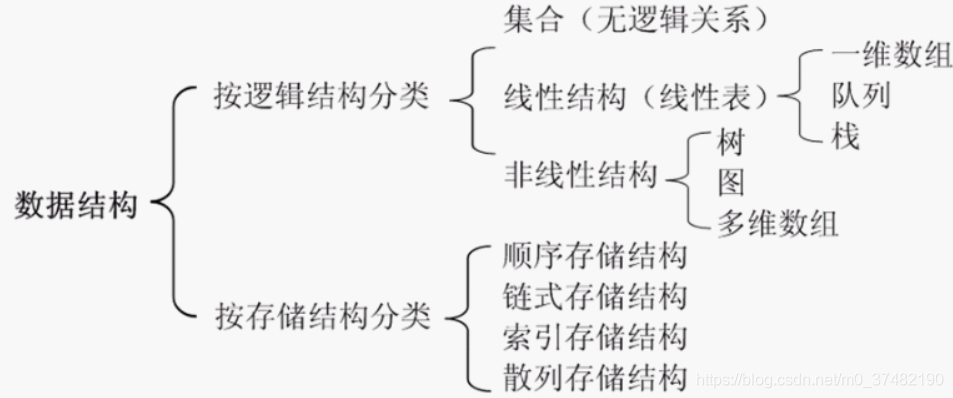
# 1. 组合数据结构概述

组合数据结构是一种将多种基本数据结构结合在一起的复杂数据结构，旨在利用不同数据结构的优势，提升数据组织、表达和算法性能。它通过将不同数据结构的特性有机结合，创建出更强大、更灵活的数据结构，满足更复杂的应用场景需求。

组合数据结构的优点包括：

- 提高数据组织效率：通过将不同数据结构组合在一起，可以根据数据的特点进行分类和组织，提高数据访问和检索效率。
- 增强数据表达能力：组合数据结构可以表示更复杂的数据关系和层次结构，增强数据表达能力，满足不同应用场景对数据表示的需求。
- 提升算法性能：通过合理组合数据结构，可以优化算法的执行效率，减少算法的时间复杂度和空间复杂度。

# 2. 组合数据结构的优势

组合数据结构通过将不同的数据结构组合在一起，可以充分发挥每种数据结构的优势，从而获得更强大的数据组织和处理能力。其主要优势体现在以下三个方面：

### 2.1 提高数据组织效率

组合数据结构可以有效地组织和管理复杂的数据，提高数据组织效率。例如，在处理具有层次结构的数据时，可以使用树形结构来组织数据，并通过链表将同级节点连接起来。这种组合方式可以同时利用树形结构的层次关系和链表的快速查找特性，高效地组织和访问数据。

### 2.2 增强数据表达能力

组合数据结构可以增强数据表达能力，使数据能够以更灵活和直观的方式表示。例如，在处理具有多重关系的数据时，可以使用图形结构来表示数据之间的关联关系。这种组合方式可以清晰地展示数据之间的相互作用，便于对数据进行分析和处理。

### 2.3 提升算法性能

组合数据结构可以提升算法性能，提高算法的效率。例如，在需要快速查找和插入数据的场景中，可以使用哈希表和链表的组合。哈希表可以快速查找数据，而链表可以高效地插入和删除数据。这种组合方式可以同时利用哈希表的快速查找和链表的动态插入特性，提升算法的性能。

#### 代码示例

# 使用树形结构和链表组合组织具有层次结构的数据

class Node:
    def __init__(self, data):
        self.data = data
        self.children = []

class Tree:
    def __init__(self):
        self.root = None

# 创建一个树形结构
tree = Tree()
root = Node("Root")
tree.root = root
child1 = Node("Child1")
child2 = Node("Child2")
root.children.append(child1)
root.children.append(child2)

# 使用链表将同级节点连接起来
child1.next = child2

# 遍历树形结构并打印数据
def print_tree(node):
    print(node.data)
    for child in node.children:
        print_tree(child)

print_tree(tree.root)

#### 代码逻辑分析

上述代码示例中，使用树形结构和链表的组合来组织具有层次结构的数据。`Node`类表示树中的节点，包含数据和子节点列表。`Tree`类表示树的根节点。

首先，创建了一个树形结构，其中根节点为"Root"，并有两个子节点"Child1"和"Child2"。然后，使用链表将同级节点"Child1"和"Child2"连接起来。

最后，使用递归函数`print_tree`遍历树形结构并打印数据。该函数首先打印当前节点的数据，然后遍历其子节点并递归调用`print_tree`函数。

# 3. 常见的组合数据结构

### 3.1 数组和链表

数组和链表是两种最基本的线性数据结构。数组是一种连续内存块，其中每个元素都具有相同的类型和大小。链表是一种由节点组成的集合，其中每个节点包含一个数据项和指向下一个节点的指针。

**数组**

# 创建一个数组
array = [1, 2, 3, 4, 5]

# 访问数组中的元素
print(array[0])  # 输出：1

# 修改数组中的元素
array[0] = 10

# 遍历数组
for element in array:
    print(element)

**逻辑分析：**

* 创建数组时，指定了数组的元素类型和大小。
* 访问数组元素时，使用下标索引。
* 修改数组元素时，使用下标索引。
* 遍历数组时，使用 for 循环。

**链表**

# 创建一个链表节点
class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

# 创建一个链表
head = Node(1)
head.next = Node(2)
head.next.next = Node(3)

# 访问链表中的元素
current = head
while current is not None:
    print(current.data)
    current = current.next

**逻辑分析：**

* 创建链表节点时，指定了节点的数据和指向下一个节点的指针。
* 创建链表时，指定了链表的头节点。
* 访问链表元素时，使用 while 循环遍历链表。
* 修改链表元素时，使用 next 指针。

### 3.2 栈和队列

栈和队列是两种重要的非线性数据结构。栈遵循后进先出 (LIFO) 原则，而队列遵循先进先出 (FIFO) 原则。

**栈**

# 创建一个栈
stack = []

# 入栈操作
stack.append(1)
stack.append(2)
stack.append(3)

# 出栈操作
print(stack.pop())  # 输出：3
print(stack.pop())  # 输出：2
print(stack.pop())  # 输出：1

**逻辑分析：**

* 创建栈时，使用空列表。
* 入栈操作时，使用 append() 方法。
* 出栈操作时，使用 pop() 方法。

**队列**

# 创建一个队列
queue = []

# 入队操作
queue.append(1)
queue.append(2)
queue.append(3)

# 出队操作
print(queue.pop(0))  # 输出：1
print(queue.pop(0))  # 输出：2
print(queue.pop(0))  # 输出：3

**逻辑分析：**

* 创建队列时，使用空列表。
* 入队操作时，使用 append() 方法。
* 出队操作时，使用 pop(0) 方法。

### 3.3 树和图

树和图是两种重要的非线性数据结构，用于表示层次结构和关系。

**树**

# 创建一个树节点
class Node:
    def __init__(self, data):
        self.data = data
        self.children = []

# 创建一棵树
root = Node(1)
root.children.append(Node(2))
root.children.append(Node(3))
root.children[0].children.append(Node(4))
root.children[0].children.append(Node(5))

# 遍历树
def traverse(node):
    print(node.data)
    for child in node.children:
        traverse(child)

traverse(root)

**逻辑分析：**

* 创建树节点时，指定了节点的数据和子节点列表。
* 创建树时，指定了树的根节点。
* 遍历树时，使用递归函数。

**图**

# 创建一个图
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': [],
    'F': []
}

# 遍历图
def traverse(graph, start):
    visited = set()
    queue = [start]

    while queue:
        current = queue.pop(0)
        if current not in visited:
            visited.add(current)
            print(current)
            for neighbor in graph[current]:
                queue.append(neighbor)

traverse(graph, 'A')

**逻辑分析：**

* 创建图时，使用字典表示节点及其相邻节点。
* 遍历图时，使用广度优先搜索 (BFS) 算法。

# 4. 组合数据结构的应用场景

组合数据结构的应用场景广泛，涵盖数据存储和管理、算法实现和优化、系统设计和开发等多个领域。

### 4.1 数据存储和管理

组合数据结构在数据存储和管理中发挥着至关重要的作用。例如：

- **关系数据库管理系统（RDBMS）**：RDBMS使用组合数据结构（如表、索引、B树）来存储和组织数据，以实现高效的数据查询和管理。
- **键值存储（Key-Value Store）**：键值存储使用哈希表或其他组合数据结构来存储键值对，提供快速的数据检索和更新。
- **文档数据库**：文档数据库使用JSON或XML等数据格式来存储文档，并使用组合数据结构（如B树、哈希表）来索引和查询文档。

### 4.2 算法实现和优化

组合数据结构在算法实现和优化中也扮演着重要的角色。例如：

- **排序算法**：归并排序、快速排序等算法使用数组或链表等组合数据结构来存储和操作数据，以实现高效的排序。
- **搜索算法**：二分查找、哈希查找等算法使用二叉树或哈希表等组合数据结构来快速查找数据。
- **图算法**：深度优先搜索、广度优先搜索等算法使用图数据结构来表示和遍历图，以解决各种图论问题。

### 4.3 系统设计和开发

组合数据结构在系统设计和开发中也有着广泛的应用。例如：

- **操作系统**：操作系统使用队列、栈等组合数据结构来管理进程和线程，实现任务调度和内存管理。
- **网络协议**：网络协议使用树、图等组合数据结构来表示网络拓扑和路由信息，实现数据传输和网络通信。
- **分布式系统**：分布式系统使用哈希表、一致性哈希等组合数据结构来实现数据分片和分布式协调，确保数据的一致性和可用性。

**示例代码：**

# 使用哈希表实现键值存储

import hashlib

class KeyValueStore:
    def __init__(self):
        self.store = {}

    def put(self, key, value):
        key_hash = hashlib.sha256(key.encode()).hexdigest()
        self.store[key_hash] = value

    def get(self, key):
        key_hash = hashlib.sha256(key.encode()).hexdigest()
        return self.store.get(key_hash)

**逻辑分析：**

该代码使用哈希表实现了一个简单的键值存储。它将键哈希化为一个唯一的字符串，并使用哈希表将哈希值映射到相应的值。`put()`方法用于存储键值对，`get()`方法用于检索值。

**参数说明：**

- `key`: 要存储或检索的键。
- `value`: 要存储的值（仅适用于`put()`方法）。

# 5. 组合数据结构的实践指南

### 5.1 选择合适的数据结构

在实际应用中，选择合适的数据结构是至关重要的。不同的数据结构具有不同的特性和优势，因此需要根据具体需求进行选择。以下是一些选择准则：

- **数据类型：**考虑要存储的数据类型。例如，数组适合存储同类型的数据元素，而链表可以存储不同类型的数据元素。
- **数据访问模式：**分析数据访问模式。如果需要频繁访问数据元素，则数组或链表是不错的选择。如果需要快速插入或删除数据元素，则栈或队列更合适。
- **数据组织方式：**考虑数据组织方式。如果数据需要按顺序组织，则数组或链表是合适的。如果数据需要按层次结构组织，则树或图更合适。

### 5.2 优化数据结构的性能

优化数据结构的性能至关重要，可以提高应用程序的整体效率。以下是一些优化技巧：

- **选择合适的算法：**选择高效的算法来操作数据结构。例如，使用二分查找算法来搜索数组中的元素比线性查找算法更有效。
- **减少不必要的操作：**避免不必要的操作，例如频繁的插入或删除操作。通过预分配内存或使用缓存技术来减少操作次数。
- **利用数据结构的特性：**利用数据结构的特性来优化性能。例如，利用数组的连续内存布局来提高数据访问速度。

### 5.3 维护数据结构的完整性

维护数据结构的完整性对于确保数据的准确性和可靠性至关重要。以下是一些维护完整性的方法：

- **验证输入数据：**在插入数据之前，验证输入数据是否有效。例如，检查数组索引是否超出范围，或检查链表节点是否为空。
- **使用错误处理机制：**在操作数据结构时，使用错误处理机制来处理异常情况。例如，在删除链表节点时，处理节点不存在的情况。
- **定期检查数据结构：**定期检查数据结构的完整性，以确保数据没有被损坏或丢失。例如，使用哈希表来检查数组中是否存在重复元素。

# 6. 组合数据结构的未来展望

组合数据结构作为一种强大的数据组织和处理技术，在未来将继续发挥重要作用，并不断演进和拓展应用领域。

### 6.1 新型数据结构的探索

随着数据量和数据复杂性的不断增长，传统的数据结构可能无法满足未来的需求。因此，研究人员和开发者正在积极探索新型数据结构，以应对新的挑战。例如：

- **自适应数据结构：**可以根据数据分布和访问模式动态调整其结构，以优化性能。
- **可持久数据结构：**可以在不修改原始数据的情况下进行修改，从而实现历史数据的版本控制和并发操作。
- **并行数据结构：**专门设计用于并行计算环境，以提高数据处理效率。

### 6.2 人工智能和机器学习中的应用

人工智能和机器学习算法高度依赖于数据，组合数据结构在这些领域中扮演着至关重要的角色。通过高效组织和处理数据，组合数据结构可以：

- **提升模型训练速度：**优化数据结构可以减少数据加载和处理时间，从而加快模型训练过程。
- **提高模型准确性：**适当的数据结构可以帮助算法更好地捕获数据中的模式和关系，从而提高模型的预测准确性。
- **支持复杂数据类型：**组合数据结构可以处理各种复杂数据类型，例如图像、文本和时间序列，为人工智能和机器学习算法提供更丰富的输入。

### 6.3 云计算和分布式系统中的应用

云计算和分布式系统需要处理海量数据，并确保数据的可靠性和可用性。组合数据结构在这些环境中具有以下优势：

- **分布式数据存储：**组合数据结构可以将数据分布在多个节点上，以实现可扩展性和容错性。
- **并发数据访问：**通过使用并发数据结构，可以同时从多个节点访问和修改数据，提高系统吞吐量。
- **数据一致性保证：**组合数据结构可以提供数据一致性保证，确保在分布式环境中数据操作的正确性。