：揭秘递归与迭代的较量：优势、劣势与应用场景剖析

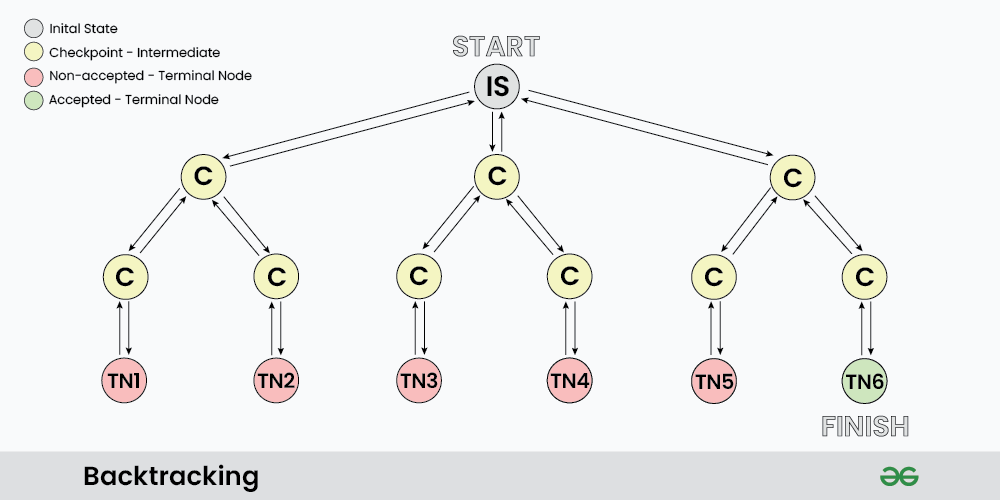
# 1. 递归与迭代概述

递归和迭代是两种常见的编程技术，用于解决各种问题。递归是一种函数调用自身的方法，而迭代使用循环来重复执行一段代码。

### 递归

递归是一种强大的技术，它可以简化代码并使其更易于理解。它通过将问题分解为更小的子问题，然后递归地解决这些子问题来工作。这种方法特别适用于树形结构和分治问题。

### 迭代

迭代是一种更有效率的技术，它使用循环来重复执行一段代码。它通过使用计数器或索引来跟踪循环次数，并根据条件判断是否继续循环。这种方法特别适用于遍历数组和链表等线性数据结构。

# 2. 递归的优势与劣势

递归是一种函数调用自身的方式，它允许函数以一种简洁优雅的方式解决复杂的问题。然而，递归也有一些缺点，例如效率低下和容易产生堆栈溢出。

### 2.1 递归的优势

#### 2.1.1 简洁优雅

递归的一个主要优势是它的简洁性。使用递归，可以将复杂的问题分解成更小的子问题，从而使代码更加清晰易读。例如，以下代码使用递归来计算阶乘：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

这段代码通过不断调用自身来计算阶乘。它首先检查 n 是否为 0，如果是，则返回 1。否则，它将 n 乘以调用自身并传入 n-1 的结果。这种方法使代码非常简洁，因为它只包含几个简单的步骤。

#### 2.1.2 易于理解

递归代码通常比迭代代码更容易理解。这是因为递归代码遵循自然语言的结构，即一个函数调用自身来解决问题。例如，以下代码使用迭代来计算阶乘：

def factorial(n):
    result = 1
    for i in range(1, n+1):
        result *= i
    return result

这段代码使用 for 循环来计算阶乘。它首先将结果初始化为 1，然后遍历从 1 到 n 的所有数字，并将每个数字乘以结果。这种方法虽然也能计算阶乘，但它比递归代码更难理解，因为它需要读者理解 for 循环的机制。

### 2.2 递归的劣势

#### 2.2.1 效率低下

递归的一个主要缺点是它的效率低下。这是因为递归函数在每次调用自身时都会创建一个新的栈帧。当递归深度较大时，这会导致堆栈溢出。例如，以下代码使用递归来计算斐波那契数列：

def fibonacci(n):
    if n == 0 or n == 1:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

这段代码通过不断调用自身来计算斐波那契数列。它首先检查 n 是否为 0 或 1，如果是，则返回 1。否则，它将调用自身两次，一次传入 n-1，一次传入 n-2，并将两个结果相加。这种方法效率很低，因为对于 n 较大的值，它需要进行大量的递归调用。

#### 2.2.2 容易产生堆栈溢出

递归的另一个缺点是它容易产生堆栈溢出。这是因为递归函数在每次调用自身时都会创建一个新的栈帧。当递归深度较大时，这会导致堆栈溢出。例如，以下代码使用递归来遍历一个树形结构：

def traverse_tree(node):
    if node is None:
        return
    else:
        traverse_tree(node.left)
        traverse_tree(node.right)

这段代码通过不断调用自身来遍历一个树形结构。它首先检查节点是否为 None，如果是，则返回。否则，它将调用自身两次，一次传入左子节点，一次传入右子节点。这种方法容易产生堆栈溢出，因为对于一个深度较大的树，它需要进行大量的递归调用。

# 3.1 迭代的优势

**3.1.1 效率高**

迭代的效率通常比递归更高，因为迭代不需要为每个递归调用分配新的栈空间。在递归中，每次调用函数都会创建一个新的栈帧，其中包含函数的参数、局部变量和返回地址。这些栈帧会在函数返回时被释放，但它们在函数执行期间会占用内存空间。

相比之下，迭代使用循环来实现相同的任务，而循环不需要创建新的栈帧。循环只需要一个计数器变量来跟踪当前迭代，并且这个变量在循环结束时会被释放。因此，迭代的内存开销比递归要小，这使得它在处理大型数据集时更有效率。

**3.1.2 不容易产生堆栈溢出**

堆栈溢出是指当函数调用的深度超过了系统允许的最大深度时发生的一种错误。在递归中，如果递归调用太多，就会发生堆栈溢出。这是因为每个递归调用都会创建一个新的栈帧，而栈帧的内存空间是有限的。

迭代不会产生堆栈溢出，因为循环不需要创建新的栈帧。循环只需要一个计数器变量来跟踪当前迭代，并且这个变量在循环结束时会被释放。因此，迭代在处理大型数据集时不容易产生堆栈溢出。

### 3.2 迭代的劣势

**3.2.1 代码复杂度高**

迭代的代码通常比递归的代码复杂度更高。这是因为迭代需要使用循环和条件语句来实现相同的任务，而递归只需要使用函数调用。

例如，以下代码使用递归计算阶乘：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

以下代码使用迭代计算阶乘：

def factorial(n):
    result = 1
    for i in range(1, n+1):
        result *= i
    return result

如你所见，迭代版本的代码比递归版本的代码更复杂。它需要使用一个循环和一个计数器变量来跟踪当前迭代。

**3.2.2 不易于理解**

迭代的代码通常比递归的代码更难理解。这是因为迭代需要使用循环和条件语句来实现相同的任务，而递归只需要使用函数调用。

例如，对于不熟悉递归的人来说，以下代码可能很难理解：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

相比之下，以下代码更容易理解：

def factorial(n):
    result = 1
    for i in range(1, n+1):
        result *= i
    return result

因此，迭代的代码通常比递归的代码更难理解。

# 4. 递归与迭代的应用场景

### 4.1 递归的应用场景

递归是一种将问题分解为更小规模的相同问题的技术，它在某些场景下具有独特的优势：

- **遍历树形结构：**树形结构是一种分层的数据结构，每个节点可以有多个子节点。递归可以轻松地遍历树形结构，因为它可以将遍历子节点的任务分解为更小的遍历任务。例如，遍历二叉树时，递归可以将遍历左子树和右子树的任务分解为更小的遍历任务。

- **求阶乘：**阶乘是一种数学运算，它将一个正整数乘以其所有较小的正整数。递归可以轻松地计算阶乘，因为它可以将计算阶乘的任务分解为计算较小阶乘的任务。例如，计算 5 的阶乘时，递归可以将计算 5 的阶乘的任务分解为计算 4 的阶乘的任务，依此类推。

### 4.2 迭代的应用场景

迭代是一种逐个处理问题的技术，它在某些场景下具有独特的优势：

- **遍历数组：**数组是一种线性数据结构，它包含一系列元素。迭代可以轻松地遍历数组，因为它可以逐个访问数组中的元素。例如，遍历一个包含 10 个元素的数组时，迭代可以逐个访问数组中的每个元素。

- **求斐波那契数列：**斐波那契数列是一种数学数列，其中每个数是前两个数的和。迭代可以轻松地计算斐波那契数列，因为它可以逐个计算数列中的每个数。例如，计算斐波那契数列中的第 10 个数时，迭代可以逐个计算数列中的前 10 个数。

**代码示例：**

# 递归求阶乘
def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

# 迭代求斐波那契数列
def fibonacci(n):
    a, b = 0, 1
    for i in range(n):
        a, b = b, a + b
    return a

**逻辑分析：**

- `factorial` 函数使用递归来计算阶乘。如果 `n` 等于 0，则返回 1。否则，返回 `n` 乘以 `n-1` 的阶乘。
- `fibonacci` 函数使用迭代来计算斐波那契数列。它将 `a` 和 `b` 初始化为 0 和 1。然后，它遍历范围为 `n` 的循环。在每个循环中，它将 `a` 和 `b` 更新为 `b` 和 `a` 加 `b`。最后，它返回 `a`。

**参数说明：**

- `factorial` 函数接受一个参数 `n`，表示要计算阶乘的正整数。
- `fibonacci` 函数接受一个参数 `n`，表示要计算斐波那契数列中第 `n` 个数。

# 5. 递归与迭代的实战案例

### 5.1 递归求解汉诺塔问题

汉诺塔问题是一个经典的递归问题，其规则如下：

* 有三根杆子，A、B、C。
* 杆子上穿有不同大小的圆盘，从上到下按从小到大排列。
* 一次只能移动一个圆盘。
* 大圆盘不能放在小圆盘上。

目标是将所有圆盘从杆子 A 移动到杆子 C。

使用递归算法求解汉诺塔问题，可以将问题分解为以下子问题：

1. 将 n-1 个圆盘从杆子 A 移动到杆子 B。
2. 将最大的圆盘从杆子 A 移动到杆子 C。
3. 将 n-1 个圆盘从杆子 B 移动到杆子 C。

递归算法的实现代码如下：

def hanoi(n, a, b, c):
    """
    递归求解汉诺塔问题

    :param n: 圆盘数量
    :param a: 起始杆子
    :param b: 中间杆子
    :param c: 目标杆子
    """
    if n == 1:
        print(f"将圆盘 {n} 从杆子 {a} 移动到杆子 {c}")
    else:
        # 将 n-1 个圆盘从杆子 A 移动到杆子 B
        hanoi(n-1, a, c, b)
        # 将最大的圆盘从杆子 A 移动到杆子 C
        print(f"将圆盘 {n} 从杆子 {a} 移动到杆子 {c}")
        # 将 n-1 个圆盘从杆子 B 移动到杆子 C
        hanoi(n-1, b, a, c)

**代码逻辑分析：**

* 函数 `hanoi` 接受四个参数：`n`（圆盘数量）、`a`（起始杆子）、`b`（中间杆子）、`c`（目标杆子）。
* 如果 `n` 等于 1，则直接将圆盘 1 从杆子 `a` 移动到杆子 `c`。
* 否则，递归调用 `hanoi` 函数三次：
* 第一次调用：将 `n-1` 个圆盘从杆子 `a` 移动到杆子 `c`，使用 `b` 作为中间杆子。
* 第二次调用：将最大的圆盘从杆子 `a` 移动到杆子 `c`。
* 第三次调用：将 `n-1` 个圆盘从杆子 `b` 移动到杆子 `c`，使用 `a` 作为中间杆子。

### 5.2 迭代求解汉诺塔问题

使用迭代算法求解汉诺塔问题，需要使用栈来存储移动步骤。

迭代算法的实现代码如下：

def hanoi_iterative(n, a, b, c):
    """
    迭代求解汉诺塔问题

    :param n: 圆盘数量
    :param a: 起始杆子
    :param b: 中间杆子
    :param c: 目标杆子
    """
    # 初始化栈
    stack = [(n, a, c, b)]

    while stack:
        # 从栈中弹出当前移动步骤
        n, a, c, b = stack.pop()

        # 如果 n 等于 1，则直接将圆盘 1 从杆子 a 移动到杆子 c
        if n == 1:
            print(f"将圆盘 {n} 从杆子 {a} 移动到杆子 {c}")
        else:
            # 将 n-1 个圆盘从杆子 a 移动到杆子 b
            stack.append((n-1, a, b, c))
            # 将最大的圆盘从杆子 a 移动到杆子 c
            print(f"将圆盘 {n} 从杆子 {a} 移动到杆子 {c}")
            # 将 n-1 个圆盘从杆子 b 移动到杆子 c
            stack.append((n-1, b, c, a))

**代码逻辑分析：**

* 函数 `hanoi_iterative` 接受四个参数：`n`（圆盘数量）、`a`（起始杆子）、`b`（中间杆子）、`c`（目标杆子）。
* 初始化一个栈，并将其压入第一个移动步骤：将 `n` 个圆盘从杆子 `a` 移动到杆子 `c`，使用 `b` 作为中间杆子。
* 进入 while 循环，循环条件为栈不为空。
* 从栈中弹出当前移动步骤，并将其解压为 `n`、`a`、`c` 和 `b`。
* 如果 `n` 等于 1，则直接将圆盘 1 从杆子 `a` 移动到杆子 `c`。
* 否则，将以下两个移动步骤压入栈中：
* 将 `n-1` 个圆盘从杆子 `a` 移动到杆子 `b`。
* 将最大的圆盘从杆子 `a` 移动到杆子 `c`。
* 重复步骤 3 和 4，直到栈为空。

# 6.1 理论比较

### 效率

递归算法的效率通常低于迭代算法。这是因为递归算法需要不断地调用自身，而每次调用都会产生额外的开销，包括函数调用、参数传递和栈帧分配。而迭代算法则不需要这些额外的开销，因此效率更高。

### 内存消耗

递归算法的内存消耗通常高于迭代算法。这是因为递归算法需要为每次调用创建一个新的栈帧，而栈帧中存储着函数的参数、局部变量和返回地址。而迭代算法则不需要创建栈帧，因此内存消耗更低。

### 代码复杂度

递归算法的代码复杂度通常高于迭代算法。这是因为递归算法的代码结构更复杂，需要考虑递归调用的终止条件和递归调用的次数。而迭代算法的代码结构更简单，只需要考虑循环条件和循环次数。

### 易于理解

递归算法的易于理解程度通常低于迭代算法。这是因为递归算法的代码结构更复杂，需要考虑递归调用的终止条件和递归调用的次数。而迭代算法的代码结构更简单，更容易理解。

## 6.2 实践比较

在实际应用中，递归算法和迭代算法各有优劣。

### 递归算法的优势

* **简洁优雅：**递归算法的代码通常更简洁优雅，更容易理解。
* **易于实现：**递归算法的实现通常更简单，不需要考虑循环条件和循环次数。

### 递归算法的劣势

* **效率低下：**递归算法的效率通常低于迭代算法，尤其是当递归深度较大时。
* **容易产生堆栈溢出：**递归算法容易产生堆栈溢出，尤其是当递归深度较大时。

### 迭代算法的优势

* **效率高：**迭代算法的效率通常高于递归算法，尤其是当数据量较大时。
* **不容易产生堆栈溢出：**迭代算法不容易产生堆栈溢出，因为迭代算法不需要创建栈帧。

### 迭代算法的劣势

* **代码复杂度高：**迭代算法的代码复杂度通常高于递归算法，因为需要考虑循环条件和循环次数。
* **不易于理解：**迭代算法的代码结构通常更复杂，不易于理解。

因此，在选择递归算法还是迭代算法时，需要根据具体问题具体分析，权衡算法的效率、内存消耗、代码复杂度和易于理解程度等因素。