：机器学习算法的递归与迭代：决策树与神经网络的奥秘

# 1. 机器学习算法基础**

机器学习算法是计算机程序，它们能够从数据中学习，并对新数据做出预测或决策。机器学习算法可以分为两大类：递归算法和迭代算法。

递归算法通过重复调用自身来解决问题。在决策树中，递归算法用于构建树形结构，其中每个节点代表一个特征，每个分支代表一个特征值。

迭代算法通过重复执行一系列步骤来解决问题。在神经网络中，迭代算法用于训练网络，其中网络权重在每次迭代中都得到更新。

# 2. 递归算法在决策树中的应用

### 2.1 决策树的概念和原理

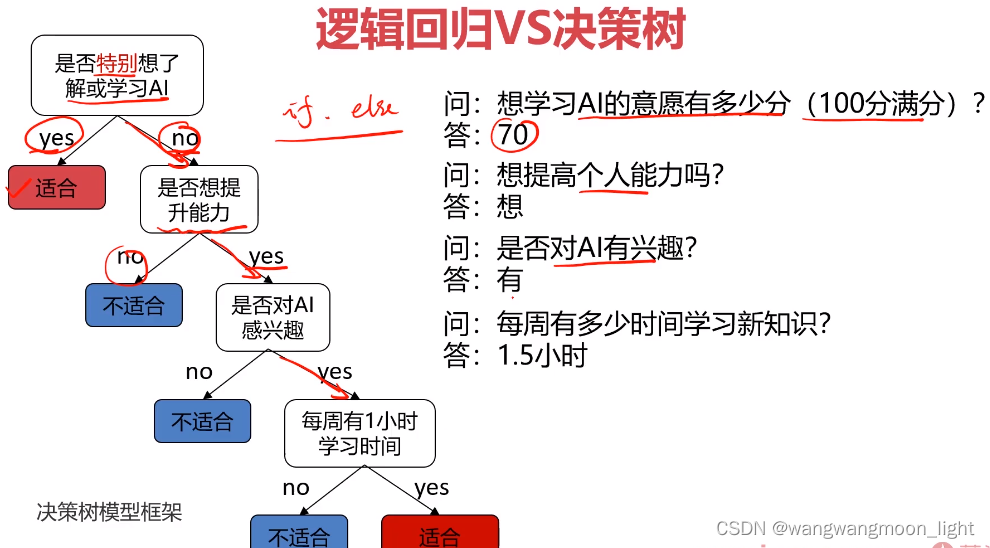
决策树是一种监督式机器学习算法，用于对数据进行分类或回归。它通过一系列规则将数据样本划分为不同的子集，每个子集对应一个类标签或回归值。

决策树的结构类似于一棵树，其中每个内部节点表示一个特征，每个分支表示该特征的可能值，每个叶节点表示一个类标签或回归值。

### 2.2 递归算法在决策树构建中的作用

递归算法在决策树构建中扮演着至关重要的角色。它通过以下步骤迭代地构建决策树：

1. **选择根节点：**从数据集中选择一个特征作为根节点，该特征具有最高的**信息增益**或**信息增益比**。
2. **划分数据集：**根据根节点特征的值将数据集划分为多个子集。
3. **递归构建子树：**对每个子集递归应用步骤 1 和 2，直到所有子集都成为纯净的，即只包含一个类标签或回归值。

### 2.2.1 ID3算法

ID3（Iterative Dichotomiser 3）算法是一种经典的决策树算法，它使用信息增益作为特征选择准则。信息增益衡量了一个特征在区分不同类标签方面的信息量。

**ID3算法步骤：**

1. 计算每个特征的信息增益。
2. 选择具有最高信息增益的特征作为根节点。
3. 根据根节点特征的值划分数据集。
4. 对每个子集递归应用步骤 1-3，直到所有子集都成为纯净的。

### 2.2.2 C4.5算法

C4.5算法是ID3算法的扩展，它使用信息增益比作为特征选择准则。信息增益比考虑了特征值的分布，使其在处理具有大量离散值的特征时更加鲁棒。

**C4.5算法步骤：**

1. 计算每个特征的信息增益比。
2. 选择具有最高信息增益比的特征作为根节点。
3. 根据根节点特征的值划分数据集。
4. 对每个子集递归应用步骤 1-3，直到所有子集都成为纯净的。

### 2.3 决策树的剪枝和优化

为了防止决策树过度拟合训练数据，需要对决策树进行剪枝和优化。

**2.3.1 预剪枝**

预剪枝是在决策树构建过程中进行的。它通过在达到一定深度或满足其他停止条件时停止进一步划分数据集来防止决策树过度增长。

**2.3.2 后剪枝**

后剪枝是在决策树构建完成后进行的。它通过移除不重要的分支来减少决策树的复杂度。

# 3. 迭代算法在神经网络中的应用

### 3.1 神经网络的概念和结构

神经网络是一种受生物神经网络启发的机器学习模型，旨在识别复杂模式并做出预测。它由相互连接的神经元组成，每个神经元接收输入、应用激活函数并产生输出。

神经网络通常由以下层组成：

- **输入层：**接收原始数据。
- **隐藏层：**处理输入数据并提取特征。
- **输出层：**生成预测或分类结果。

### 3.2 迭代算法在神经网络训练中的作用

神经网络的训练是一个迭代过程，涉及调整网络权重以最小化损失函数。迭代算法用于更新权重，使网络能够从数据中学习。

#### 3.2.1 反向传播算法

反向传播算法是一种广泛使用的迭代算法，用于训练神经网络。它通过计算损失函数对权重的梯度来更新权重。

**代码块：**

import numpy as np

def backpropagation(model, X, y, epochs=100, learning_rate=0.01):
    for epoch in range(epochs):