【误差度量方法比较】：均方误差与其他误差度量的全面比较

# 1. 误差度量方法的基本概念

误差度量是评估模型预测准确性的关键手段。在数据科学与机器学习领域中，我们常常需要借助不同的指标来衡量预测值与真实值之间的差异大小，而误差度量方法就是用于量化这种差异的技术。理解误差度量的基本概念对于选择合适的评估模型至关重要。本章将介绍误差度量方法的基础知识，包括误差类型、度量原则和它们在不同场景下的适用性。

## 1.1 误差度量的重要性

在数据分析和模型训练过程中，误差度量方法是用来判断模型性能好坏的主要手段。一个有效的误差度量方法不仅能够帮助我们了解模型对数据的拟合程度，还能够指导我们进行模型优化。选择合适的误差度量可以让我们更准确地反映预测问题的本质。

## 1.2 误差的分类

误差分为系统误差和随机误差两大类。系统误差通常是由于模型假设或数据收集过程中的偏差导致的，而随机误差则是由数据的自然变异所引起的。正确的误差度量方法能够帮助我们区分这两种误差，并采取相应的改进措施。

## 1.3 度量原则

在选择误差度量方法时，需要遵循几个基本原则：首先，度量方法应当能够准确反映模型预测与真实值之间的差异；其次，它需要适用于特定的数据分布；最后，度量方法应当便于计算，能适用于大规模数据集。

通过上述内容，我们对误差度量方法的基本概念有了初步的了解。在后续章节中，我们将深入探讨具体的误差度量方法，如均方误差（MSE）等，并分析它们的计算和应用。

# 2. 均方误差（MSE）的理论基础与计算

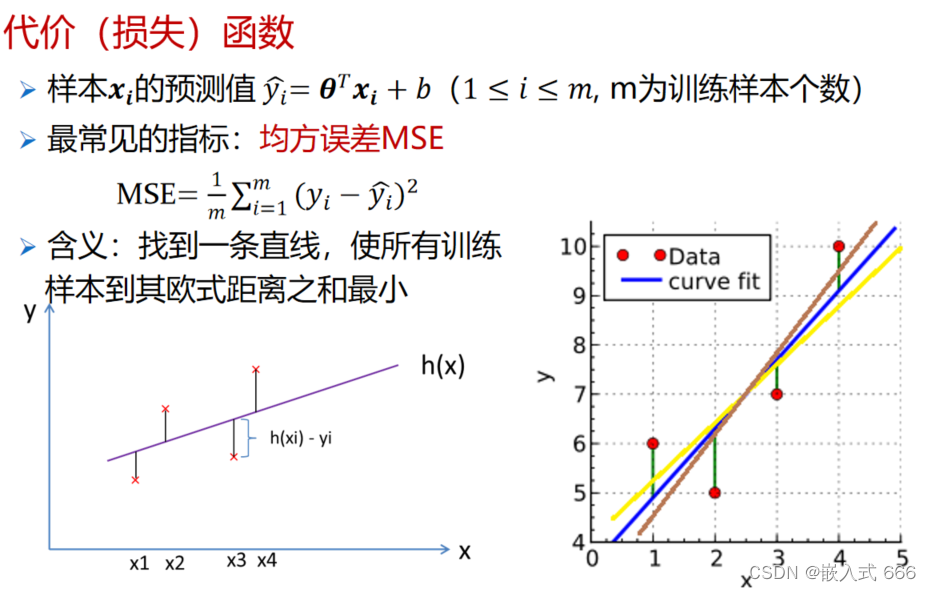
均方误差（MSE，Mean Squared Error）是衡量预测模型性能的一个重要指标。它通过计算真实值与预测值之间差的平方的平均值来评估模型的准确性。MSE 对于大误差给予更大的惩罚，因而在很多统计建模和预测问题中被广泛使用。

## 2.1 均方误差定义和数学表达

### 2.1.1 基本定义

均方误差是从多个误差值中计算出来的统计量，它能够反映模型预测值与实际值之间的偏差程度。其核心思想在于对各个误差项平方后求平均，从而得到一个可以评估误差大小的数值。

### 2.1.2 数学公式解析

均方误差的数学定义是：

\[ MSE = \frac{1}{n}\sum_{i=1}^{n}(Y_i - \hat{Y}_i)^2 \]

这里，\(Y_i\) 表示实际观测值，\(\hat{Y}_i\) 表示预测值，\(n\) 表示观测的样本数量。误差项 \((Y_i - \hat{Y}_i)^2\) 代表第 \(i\) 个观测值的预测误差的平方。

在实际应用中，MSE 可以用于衡量回归模型的性能，也常被用作优化算法的目标函数，如梯度下降法中，目标就是最小化MSE。

## 2.2 均方误差的特性分析

### 2.2.1 统计性质

均方误差具有以下统计性质：

- **无偏性**：如果一个估计是无偏的，则其期望值等于待估计的参数的真实值。
- **一致性**：随着样本数量 \(n\) 增加，估计值会趋向于真实的参数值。
- **可分解性**：在某些条件下，MSE 可以分解为方差和偏差的平方之和，有助于分析模型的偏差-方差权衡。

### 2.2.2 应用场景

MSE 在以下场景中应用广泛：

- **模型评估**：在统计学和机器学习中，评估模型对未知数据的预测能力。
- **参数估计**：估计模型参数时作为损失函数，最小化MSE来寻找最优参数。

### 2.2.3 优缺点总结

MSE 的优点包括：

- 易于理解和计算。
- 对大误差进行惩罚，有助于提高预测精度。

然而，MSE 的缺点也是显而易见的：

- 对异常值非常敏感，因为其对误差的平方会放大大误差的影响。
- 在数据中存在异常值的情况下，MSE 可能不是一个良好的性能指标。

## 2.3 均方误差计算的实践应用

### 2.3.1 具体计算步骤

使用均方误差对模型进行性能评估的具体步骤包括：

1. 收集一组观测值 \(Y_i\) 和对应的模型预测值 \(\hat{Y}_i\)。
2. 对每对实际值和预测值，计算误差 \(e_i = Y_i - \hat{Y}_i\)。
3. 计算每个误差的平方 \(e_i^2\)。
4. 对所有的误差平方值进行求和，然后除以观测值的总数 \(n\)。
5. 得到的结果即为均方误差值。

### 2.3.2 应用实例分析

假设有一个简单的线性回归模型，用来预测某地区未来一年内的平均气温。模型的预测值和实际观测值如下：

| 月份 | 实际气温 \(Y_i\) | 预测气温 \(\hat{Y}_i\) |
|------|------------------|----------------------|
| 1月 | 10°C | 9°C |
| 2月 | 12°C | 11°C |
| ... | ... | ... |
| 12月 | 11°C | 10°C |

我们可以使用上述步骤来计算MSE：

import numpy as np

# 真实值和预测值
actual_temps = np.array([10, 12, ... ,