【从零到MSE英雄】：统计学视角下的均方误差全面解析

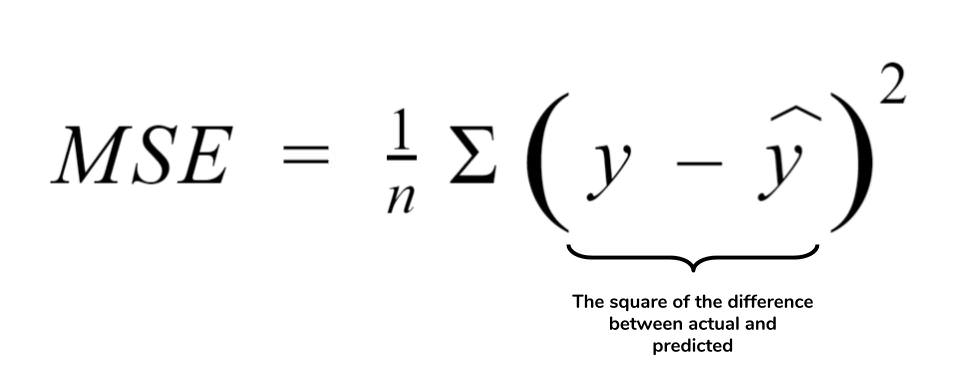
# 1. 均方误差的定义与统计学基础

## 1.1 均方误差的基本概念

均方误差（Mean Squared Error, MSE）是评估预测模型性能的一个重要指标，它衡量的是模型预测值与实际值之间差异的平均度量。数学上，它是所有误差平方的平均值，这使得大误差比小误差在总误差中占有更大的权重。MSE的计算公式为：

MSE = \frac{1}{n} \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2

其中，`Y_i`代表实际值，`\hat{Y}_i`代表预测值，`n`是样本的总数。从公式可以看出，MSE实质上是误差的平方和除以样本数量。

## 1.2 统计学中的应用

在统计学中，MSE不仅仅是一个衡量标准，它还与方差和标准差紧密相关，可以看作方差的一个特例。若将预测模型视为一个随机变量，MSE则可以用来描述这个随机变量的离散程度。它还有助于统计推断，例如，在线性回归分析中，最小化MSE是寻找最佳拟合线的重要步骤。

MSE还与最小二乘法紧密相关。最小二乘法试图找到一组参数，使得拟合模型和数据之间的MSE达到最小。这一方法在参数估计、曲线拟合以及统计模型中应用极为广泛。

## 1.3 为何使用均方误差

使用MSE作为评价标准有其独特的优势。首先，由于MSE考虑了误差的平方，因此它会给予较大的误差更高的惩罚，这有利于对极端误差敏感的应用场景。其次，MSE与方差和标准差的直接关系使得它在统计学中易于理解和应用。最后，从优化的角度来看，MSE作为一个连续可微的函数，方便了梯度下降等优化算法的实现。

不过，需要注意的是，MSE并不适合所有的应用场合，特别是当数据中含有异常值时，MSE可能会受到较大影响，因为较大的误差会被过分放大。因此，在实际应用中，需要根据具体情况来决定是否使用MSE，或者考虑使用其他误差度量方式作为补充。

# 2. 均方误差的理论与计算方法

均方误差（Mean Squared Error, MSE）是一种衡量模型预测误差的统计量，广泛应用于各种统计学和机器学习算法中。MSE是观测值与真实值之间差的平方的平均值，它能够给出预测误差大小的直观概念，并对预测模型的性能进行评估。本章将深入探讨均方误差的理论基础、计算方法以及与相关统计学概念的关联。

### 2.1 均方误差的数学表达与意义

#### 2.1.1 均方误差的推导与公式

MSE定义为预测值与实际值差值的平方和的平均值。在数学表达上，对于一组n个观测数据，其真实值为\( y_i \) (其中 \( i = 1, 2, ..., n \))，模型预测值为 \( \hat{y}_i \)，均方误差的计算公式为：

\[ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]

其中，差值 \( (y_i - \hat{y}_i) \) 代表单个预测误差，通过平方，我们消除了误差的正负符号，使得所有的误差项都是非负的。MSE的计算过程实质上是测量模型预测值与真实值之间的偏差程度，并对这些偏差进行放大，以此来强调较大的预测误差。

#### 2.1.2 均方误差在预测中的应用

在预测任务中，尤其是回归分析中，均方误差是一个非常重要的评价指标。它能够反映模型对数据的拟合程度。一个低的MSE表明模型的预测值接近于真实值，反之则表明模型的预测能力较弱。

当我们拥有多组模型进行比较时，选择具有最小均方误差的模型，通常意味着该模型在预测上具有更高的准确度。通过计算不同模型的MSE值，可以直观地比较模型之间的预测性能，帮助我们进行模型选择和调优。

### 2.2 均方误差与其他误差度量的比较

#### 2.2.1 均方误差与绝对误差

在选择适当的误差度量指标时，均方误差并不是唯一的标准。绝对误差（Mean Absolute Error, MAE）是另一种常用的误差度量方法，它计算的是预测误差的绝对值的平均值，公式如下：

\[ MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| \]

与均方误差相比，绝对误差对异常值的敏感度较低，因为平方和开方的过程会放大较大的误差值。MSE对预测误差中的异常值更加敏感，因此在包含异常值的数据集上，MSE可能会受到较大影响。

#### 2.2.2 均方误差与平均绝对误差

在实际应用中，MSE和MAE各有优劣，选择哪一种作为评价指标需根据具体问题和数据的特性来决定。MAE的计算和解读较为简单直观，而MSE对模型的预测准确性要求更高，因此在评估模型性能时可能更为严格。下面是一个简单的Python代码块，用于计算均方误差和平均绝对误差：

import numpy as np

# 真实值和预测值
y_true = np.array([3, -0.5, 2, 7])
y_pred = np.array([2.5, 0.0, 2, 8])

# 计算均方误差
mse = np.mean((y_true - y_pred) ** 2)
# 计算平均绝对误差
mae = np.mean(np.abs(y_true - y_pred))

print(f"MSE: {mse}")
print(f"MAE: {mae}")

### 2.3 均方误差的统计解释

#### 2.3.1 方差、标准差与均方误差的关系

均方误差与方差、标准差有着密切的联系。方差是衡量一组数值分散程度的统计量，定义为各数据与均值差的平方的平均值，公式为：

\[ Var(Y) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \bar{y})^2 \]

其中，\( \bar{y} \) 是观测值的均值。均方误差可以看作是对预测值 \( \hat{Y} \) 的方差，并且在预测中包含了 \( Y \) 和 \( \hat{Y} \) 之间差异的信息。

标准差则是方差的平方根，提供了一种衡量数据离散程度的尺度。在MSE和标准差之间，存在直接的数学转换关系：若 \( \sigma \) 是标准差，则 \( \sigma^2 \) 就是方差，也与MSE成正比。

#### 2.3.2 均方误差在统计推断中的作用

MSE在统计推断中扮演着重要角色。例如，在参数估计中，通过最小化MSE可以得到期望损失最小的估计量，这被称为均方误差估计（Mean Squared Error Estimator）。它不仅反映了估计量与真实值的偏差，还包括了估计的不确定性或离散程度。

在模型选择和验证时，MSE可以用来评估模型对未知数据的预测能力。通过交叉验证等方法，可以在数据集的不同子集上计算MSE，以此来评估模型在不同条件下的泛化性能。

> **注：** 在实际使用均方误差时，还需注意其对异常值的敏感性。因此，在数据中含有极端值或异常点时，可能需要对MSE的计算和解释进行调整或采用更为稳健的误差度量。

在本章节中，我们详细探讨了均方误差在理论和计算方法上的细节，以及它与其他统计度量的对比。本章不仅提供了均方误差的数学定义和统计解释，而且从实际应用的角度分析了它的优缺点。在下一章中，我们将深入均方误差在机器学习中的应用实践，并展示如何在实践中操作和优化这一重要的性能指标。

# 3. 均方误差在机器学习中的应用实践

## 3.1 均方误差在回归分析中的应用
### 3.1.1 回归模型的均方误差计算
在回归分析中，均方误差（MSE）是衡量模型预测准确性的一个关键指标。具体来说，MSE是实际观测值与模型预测值之差的平方的平均值。其数学表达式可以表示为：

\[ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]

其中，\( y_i \) 表示第 \( i \) 个观测值，\( \hat{y}_i \) 表示模型对第 \( i \) 个观测值的预测值，而 \( n \) 是数据集中的观测值总数。

在编程实现上，以Python的NumPy库为例，可以编写如下代码计算MSE：

import numpy as np

# 实际观测值
actual = np.array([1, 2