【深度学习损失选择】：均方误差与交叉熵的权衡

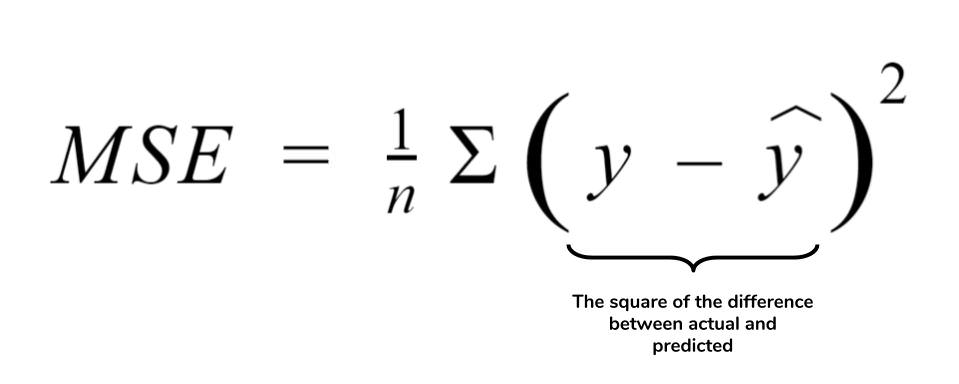
# 1. 深度学习损失函数概述

在深度学习领域中，损失函数是指导模型训练的核心组件之一。它衡量了模型预测值与真实值之间的差异，为模型提供学习信号。理解损失函数的工作机制对于构建、优化及改进深度学习模型至关重要。随着技术的发展，不同类型的损失函数被提出来满足各种任务的需求，从简单的均方误差到复杂的结构化预测损失函数。本章将为读者提供损失函数的全面概述，为进一步深入研究各个具体损失函数打下坚实基础。

# 2. 均方误差（MSE）损失的理解与应用

均方误差（Mean Squared Error, MSE）损失是机器学习中最常用的损失函数之一，特别是在回归问题的建模中。它衡量的是模型预测值与实际值之间的平均平方差。本章首先介绍均方误差损失的基本概念，接着探讨其优化算法，最后通过实际案例来展示均方误差在不同问题中的应用。

## 2.1 均方误差损失的基本概念

### 2.1.1 定义与数学表达

均方误差损失函数被定义为所有数据点上预测值与真实值差的平方的平均值。数学上，对于有N个样本的数据集，每个样本的真实值为y_i，模型预测值为\(\hat{y}_i\)，均方误差损失可以表达为：

\[ MSE = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2 \]

当N=1时，即针对单个数据点，MSE简化为：

\[ MSE = (y_i - \hat{y}_i)^2 \]

### 2.1.2 适用场景与优缺点

均方误差损失在以下场景中特别适用：

- 回归问题：MSE广泛用于回归模型的损失函数，因为其能够给出预测值与实际值之间差异的连续性度量。
- 线性模型：当使用线性回归时，MSE自然成为优化的目标函数。
- 需要避免过大误差：MSE对于较大的误差赋予了更大的权重，这有助于模型避免出现大的预测误差。

然而，MSE也有其缺点：

- 对异常值敏感：由于MSE对误差的平方操作，较大的误差会对总损失有较大的影响，从而可能使模型过于关注那些异常值。
- 梯度在误差接近0时变得很小：这可能导致在使用基于梯度的优化算法时，学习过程变得缓慢。

## 2.2 均方误差损失的优化算法

### 2.2.1 梯度下降法与MSE的关系

梯度下降法是最常用的优化算法之一，它通过计算损失函数相对于模型参数的梯度来更新参数，以实现损失函数值的最小化。在MSE的情况下，对于一个线性模型：

\[ \hat{y}_i = \theta_0 + \theta_1 x_1 + ... + \theta_n x_n \]

损失函数相对于参数\(\theta_j\)的梯度为：

\[ \frac{\partial MSE}{\partial \theta_j} = \frac{2}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)(-x_{ij}) \]

其中\(x_{ij}\)表示第i个样本的第j个特征。

### 2.2.2 正则化与MSE

为了防止模型过拟合，通常会将正则化项加入到损失函数中。对于L2正则化（也称作岭回归），损失函数将变为：

\[ MSE_{reg} = MSE + \lambda \sum_{j=1}^{n} \theta_j^2 \]

这里\(\lambda\)是正则化参数，它控制正则化项的相对重要性。正则化鼓励模型参数取较小的值，有助于改善泛化性能。

## 2.3 均方误差在实际问题中的应用案例

### 2.3.1 回归问题中的应用

在实际的回归问题中，假设我们有一组房价数据，目标是预测给定房屋的市场价值。我们首先需要收集数据，包括房屋的大小、卧室数量、地理位置等信息，并用这些特征来训练一个线性回归模型。损失函数使用MSE：

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np

# 假设X是特征矩阵，y是目标向量
model = LinearRegression()
model.fit(X, y)

# 假设X_test是测试集特征矩阵
y_pred = model.predict(X_test)

# 计算MSE
mse_loss = mean_squared_error(y_test, y_pred)
print(f'MSE Loss: {mse_loss}')

### 2.3.2 深度学习模型的性能评估

在深度学习模型中，MSE可以用作评估模型预测性能的一种方式。假设使用神经网络来预测某个连续值，MSE可以帮助衡量模型输出与真实值之间的差异：

import torch
import torch.nn as nn

# 假设是一个深度学习模型实例
class RegressionModel(nn.Module):
    def __init__(self):
        super(RegressionModel, self).__init__()
        # 定义模型结构
        self.linear = nn.Linear(in_features, out_features)

    def forward(self, x):
        return self.linear(x)

# 创建模型实例
model = RegressionModel()

# 假设 criterion 是MSE损失函数
criterion = nn.MSELoss()

# 假设预测输出和真实目标
outputs = model(inputs)
loss = criterion(outputs, targets)

print(f'MSE Loss: {loss.item()}')

### 表格：MSE与其他回归损失函数的对比

| 损失函数 | 适用场景 | 对异常值的敏感度 | 优化方法 |
|-------------|-------------------------------|-----------------