【超参数调优秘籍】：通过MSE选择最佳模型参数

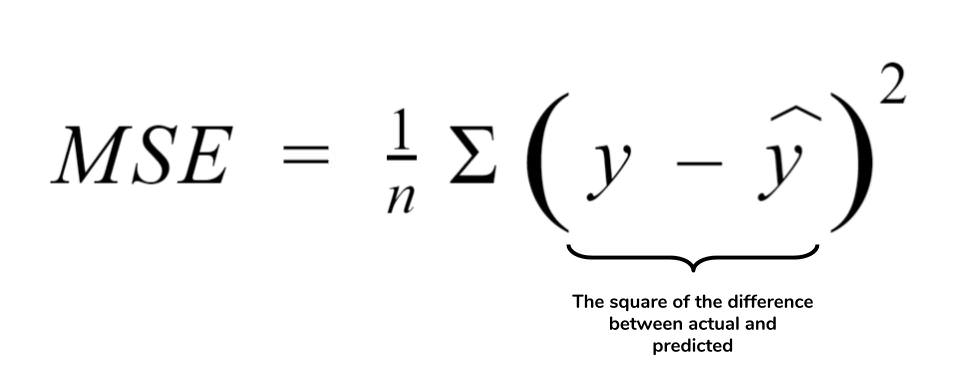
# 1. 超参数调优的基本概念

在机器学习的实践中，调优超参数是提升模型性能的关键步骤。超参数不同于模型参数，它们不能通过学习算法直接从数据中获得，而是需要根据经验和验证集的表现预先设定。超参数的调整可以在一定程度上决定模型的性能上限。

超参数调优通常涉及以下几个步骤：

1. **确定要调整的超参数**：从学习率、批处理大小、网络层数等众多可选超参数中，根据模型和任务的特定需求，选择对模型性能影响较大的超参数进行调整。
2. **选择调优策略**：如网格搜索、随机搜索或贝叶斯优化等方法，通过这些策略来减少搜索空间，快速找到较好的超参数组合。

3. **性能评估**：使用交叉验证等方法在验证集上评估超参数组合带来的模型性能，确保模型不会过拟合训练数据。

超参数调优是深度学习和机器学习领域中一个活跃的研究课题，而后续的章节将深入探讨均方误差（MSE）与超参数调优的关系，揭示如何有效利用MSE来指导和优化模型的超参数。

# 2. 均方误差（MSE）的理论与计算

### 2.1 均方误差（MSE）的数学基础

#### 2.1.1 损失函数的定义

在机器学习中，损失函数是用来衡量模型预测值与真实值之间差异的一种方法。我们希望损失函数越小越好，因为这意味着模型的预测值越接近真实值。均方误差（MSE）是最常见的损失函数之一，主要用于回归问题。

MSE的基本定义是对单个样本的误差平方，然后对所有样本取平均值。数学上，对于给定的数据集，我们假设每个样本的真实值为\(y_i\)，预测值为\(\hat{y_i}\)，则MSE定义如下：

\[
MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2
\]

其中\(n\)代表样本数量。

#### 2.1.2 均方误差（MSE）的计算公式

具体而言，MSE是一种衡量预测值\(\hat{y_i}\)与真实值\(y_i\)差异的方法。为了计算MSE，我们首先计算每个预测值与实际值之间的差值，然后将这些差值平方，最后对所有样本的平方误差求平均。

1. 计算预测值与真实值之间的差值：
\[
d_i = y_i - \hat{y_i}
\]

2. 计算每个差值的平方：
\[
e_i = d_i^2 = (y_i - \hat{y_i})^2
\]

3. 对所有平方误差求和，并计算平均值：
\[
MSE = \frac{1}{n}\sum_{i=1}^{n}e_i = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2
\]

MSE是衡量回归模型性能的一个非常重要的指标，它将模型预测的误差以二次方的形式放大，因此对大误差的惩罚更重。

### 2.2 均方误差（MSE）在模型评估中的应用

#### 2.2.1 评价回归模型的准确性

在实际的模型评估中，MSE被广泛用于判断回归模型预测的准确性。MSE的值越低，表明模型的预测结果与实际数据越接近。通常情况下，MSE越小，模型的性能被认为越好。

在模型的训练过程中，我们通常使用MSE作为优化目标，通过梯度下降等优化算法不断地调整模型参数，以期达到最小化MSE的目的。因此，MSE在模型训练和验证阶段都是一个重要的指标。

#### 2.2.2 与其他误差度量的比较

MSE并非误差度量的唯一方法。它与其他误差度量如平均绝对误差（MAE）或均方根误差（RMSE）等有着各自的优势和局限性。例如，MAE对异常值不太敏感，但MSE却可能因为较大的误差值而受到严重影响。而RMSE则是MSE的平方根形式，对误差进行了标准化，便于和原始数据进行比较。

不同的误差度量方法适用于不同的场合，MSE特别适合于需要对大误差进行较强惩罚的场景。在选择适当的误差度量方法时，需要考虑模型的特性以及问题的具体需求。

在选择损失函数时，我们还需要考虑到模型优化算法的特性。例如，一些优化算法对损失函数的形状更为敏感。因此，选择适合模型和问题的损失函数，是实现良好模型性能的关键步骤。接下来，我们将探讨如何基于MSE来选择合适的模型参数，以进一步提升模型的预测准确性。

# 3. 基于MSE的模型参数选择实践

### 3.1 模型参数对MSE的影响

#### 3.1.1 参数调整的直观理解

均方误差（MSE）作为衡量模型预测值与实际值差异的重要指标，其数值的大小直接受模型参数的影响。在使用如线性回归、神经网络等模型时，模型参数的细微改变都可以导致MSE的显著变化。直观上讲，模型参数如果设置得不恰当，可能会导致模型在训练集上过拟合或欠拟合，从而影响模型的泛化能力。

理解参数调整对MSE的影响需要从模型学习过程的内部机制着手。以线性回归为例，模型的参数实际上是学习数据特征与目标变量之间关系的权重。若权重过大，可能会导致模型对噪声过于敏感，表现为过拟合，此时MSE在训练集上可能很低，但在未见过的数据上MSE却很高。相反，若权重太小，模型则可能无法捕捉到数据中的有用信息，表现为欠拟合，导致MSE在训练集和测试集上都偏高。

#### 3.1.2 实例分析：不同参数对MSE的作用

为了具体说明参数调整对MSE的影响，我们来看一个简单的线性回归示例。假设我们有一个简单的数据集，目标是学习一个一元线性模型 `y = wx + b`，其中 `w` 是权重，`b` 是偏置。

假设初始参数为 `w=1` 和 `b=0`。此时MSE可能相对较高。为了减小MSE，我们可以尝试增加 `w` 的值，使得模型能够更好地拟合数据的趋势。但如果增加太多，可能会引起过拟合，MSE在训练集上会继续下降，但在新的测试数据上MSE可能会上升。

通过这种方式，我们可以得到一个直观的结论：MSE作为优化目标，对于参数调整是有指导意义的。但要达到最佳的泛化性能，需要在训练集上的拟合和模型复杂度之间找到一个平衡点。这种平衡点的寻找，常常是通过一种称为超参数调优的过程来实现的。

### 3.2 实用的超参数搜索策略

#### 3.2.1 网格搜索和随机搜索

在模型训练中，超参数的搜索策略至关重要。最简单直观的方法之一是网格搜索（Grid Search）。该方法通过遍历给定范围内的所有可能的参数组合，以找到最佳的超参数配置。每个参数设定都会尝试，在MSE的基础上评分并最终选出最优组合。

尽管网格搜索在概念上简单明了，但它在高维参数空间中会变得非常耗时。例如，如果有10个参数，每个参数有10个可能的值，网格搜索就需要尝试10^10次模型训练，这在实际操作中是不可行的。

随机搜索是网格搜索的一个变种，它不遍历整个参数空间，而是随机选择一定数量的点进行尝试。这可以减少计算开销，仍然有可能找到较好的超参数配置。随机搜索的理论依据在于，不是所有的参数组合都同等重要，因此随机选取参数组合的效率可能更高。

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC

# 示例代码：使用网格搜索进行超参数优化
param_grid = {
    'C': [0.1, 1, 10],
    'gamma': [0.01, 0.1, 1],
    'kernel': ['rbf']
}

grid_search = GridSearchCV(SVC(), param_grid, cv=5)
grid_search.fit(X_train, y_train)

# 输出最佳参数组合
print("Best parameters: {}".format(grid_search.best_params_))

在上述代码中，我们使用`GridSearchCV`进行了SVM模型参数的网格搜索。`param_grid`字典定义了搜索的参数范围，而`GridSearchCV`会自动进行交叉验证来找到最佳参数组合。

##