【MSE解读指南】：预测模型评估中的均方误差剖析

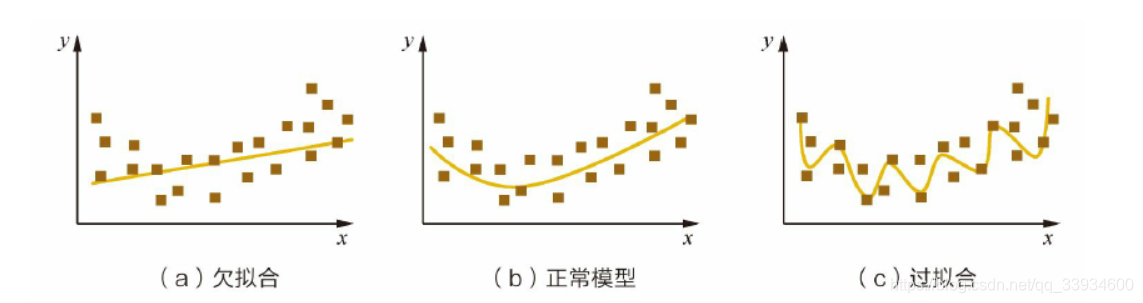
# 1. 预测模型评估的基本概念

在进行机器学习预测时，我们如何判断模型的好坏呢？答案是通过评估指标来量化模型的性能。预测模型评估是机器学习中不可或缺的一个环节，它涉及到模型的准确度、泛化能力、误差分布等多个方面。**预测模型评估的基本概念**为我们提供了一系列的标准和工具，帮助我们理解模型的表现，以及它在未知数据上的预测能力。

评估指标的选择直接影响模型的优化方向和最终效果。比如，在回归问题中，均方误差（MSE）是常用的评估指标之一，它衡量的是预测值与实际值之差的平方的平均值，能够反映出预测误差的大小。准确度高的模型应当有较小的均方误差，意味着模型预测的结果更接近真实的观测值。

为了深入理解预测模型评估，接下来的章节将详细探讨均方误差的数学原理和应用，以及如何在实践中计算和优化MSE，并且与其他性能指标进行比较。通过这些内容的学习，我们能够更好地评估和提升预测模型的性能。

# 2. 均方误差（MSE）的数学原理

均方误差（Mean Squared Error, MSE）是衡量模型预测值与实际值差异的一种常用指标，其核心思想是通过计算预测值与真实值的差的平方的平均数来度量预测性能。在本章节中，我们将从数学原理的角度深入探讨均方误差，以便读者能够更准确地理解和应用这一重要的评估工具。

## 2.1 均方误差的定义与公式

### 2.1.1 均方误差的推导过程

均方误差的计算方式非常直观，即首先计算出所有单个预测误差的平方值，然后求取这些平方误差的平均数。具体计算公式如下：

\[ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]

其中，\( n \) 表示样本的数量，\( y_i \) 是第 \( i \) 个样本的实际值，而 \( \hat{y}_i \) 是对应的预测值。通过这个公式，我们可以得到一个表示平均误差大小的数值。

推导过程中，MSE将误差的大小量化为平方项，这使得较大误差会被赋予更大的权重。因此，MSE对于那些影响较大的误差非常敏感。这种特性使得MSE在模型性能评估时能够突出较大的预测误差。

### 2.1.2 均方误差与其它误差度量的关系

MSE只是众多误差度量指标中的一种，它与绝对误差（Mean Absolute Error, MAE）、均方根误差（Root Mean Squared Error, RMSE）等指标有着密切的联系。

绝对误差是计算预测值与实际值之间差的绝对值，相比于MSE，它对误差的正负号不敏感，但同样能反映误差的大小。MAE的计算公式为：

\[ MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| \]

而RMSE是MSE的平方根，它将误差的单位调整到与原数据一致，便于理解误差的绝对大小：

\[ RMSE = \sqrt{MSE} \]

在实际应用中，选择不同的误差度量会依赖于问题的具体需求。例如，MSE适合于那些对较大误差较为敏感的情况，而MAE则更适用于对误差大小不敏感的场景。

## 2.2 均方误差的统计解释

### 2.2.1 预测误差的期望与方差

从统计学的角度来看，MSE可以分解为两个主要组成部分：误差的方差和误差的平方偏差。

\[ MSE = Var(\hat{y}) + Bias(\hat{y}, y)^2 \]

其中，\( Var(\hat{y}) \) 是预测值的方差，反映了模型预测值的不确定性；\( Bias(\hat{y}, y)^2 \) 是预测值与真实值之间差异的平方偏差，代表了模型预测的一致性。当模型的预测是一致的（即偏差小），并且具有较低的不确定性（即方差小），MSE值会较低。

### 2.2.2 均方误差的偏差-方差权衡

在预测模型中，我们经常会遇到偏差-方差权衡的问题。偏差指的是模型预测值与真实值之间的平均差异，而方差指的是预测结果的变动范围。理想情况下，我们希望模型具有低偏差和低方差。

然而，在实际中往往存在一种权衡：为了减少偏差，模型可能变得更加复杂，导致方差增加；而为了降低方差，模型可能过于简化，增加了偏差。MSE的计算可以揭示这种权衡关系，为模型选择提供了理论支持。

在接下来的章节中，我们将探讨均方误差在不同模型中的应用，以及如何在实践中实现和优化MSE。这将为读者提供一个全面的视角，了解均方误差在模型评估中的作用和如何在各种情况下合理地使用它。

# 3. 均方误差在不同模型中的应用

均方误差（MSE）是评估预测模型性能的常用指标，它衡量的是模型预测值与实际值之间差异的平方的平均值。通过MSE，我们可以量化模型误差并优化模型参数，以期达到更好的预测效果。在不同的模型中，MSE的应用及优化策略各有侧重。本章将详细介绍MSE在各个模型中的具体应用，包括线性回归、决策树与集成学习以及神经网络。

## 3.1 线性回归模型中的MSE应用

### 3.1.1 线性回归的误差分析

线性回归是最基础的回归模型，它通过构建自变量和因变量之间线性关系的模型来进行预测。在评估线性回归模型时，MSE是主要的性能度量指标之一。MSE可以通过以下公式计算：

\[ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \]

其中，\( n \) 是样本数量，\( y_i \) 是实际值，而 \( \hat{y}_i \) 是预测值。这个公式直观地表明了MSE是实际值与预测值差异平方的平均数。

### 3.1.2 MSE在模型优化中的角色

在优化线性回归模型时，MSE不仅用作性能评估，也是梯度下降算法中损失函数的直接表达。通过最小化MSE，可以找到使预测误差最小化的参数值。模型训练的目标就是找到一组参数 \( \theta \) 使得MSE最小化：

\[ \theta = \arg\min_{\theta} \sum_{i=1}^{n} (y_i - \theta^Tx_i)^2 \]

上述过程需要对每个参数 \( \theta_j \) 进行求导并更新，直至收敛到最小MSE对应的参数配置。

## 3.2 决策树与集成学习中的MSE应用

### 3.2.1 决策树模型的误差计算

决策树是另一种常用的预测模型，它通过从根到叶的决策路径来做出预测。在决策树中，MSE同样可以作为评估节点划分质量的指标。每个节点的划分目标是尽量减小子节点的MSE。具体来说，一个节点 \( t \) 的MSE定义如下：

\[ MSE_t = \sum_{i=1}^{m} \sum_{j=1}^{J} (n_{ij} \cdot (y_