【数学推导：MSE背后】：概率论视角下的均方误差

# 1. 均方误差（MSE）简介

在机器学习和统计学中，均方误差（Mean Squared Error, MSE）是衡量模型预测值与真实值之间差异的常用指标。它通过计算预测值与真实值差值的平方，再求平均值得到。这个指标对于优化回归问题有着重要应用，因为它反映了模型的精度，并且可以很容易地利用数学方法进行最小化处理。尽管MSE具有直观和易于实现的优点，但在处理异常值时需要特别注意，因为它的平方项会放大大的预测误差，这可能会导致模型对异常值过于敏感。在后续章节中，我们将深入探讨MSE与概率论的关系，以及如何在实践中有效地应用和优化MSE。

# 2. ```
# 第二章：概率论基础与MSE的联系

概率论是数学的一个分支，它研究随机事件及其发生的概率。在机器学习中，概率论被广泛应用于建模不确定性和进行预测。均方误差（MSE）作为一种常用的损失函数，在其计算过程中也涉及到概率论的多个概念。本章将探讨概率论与MSE之间的联系，从随机变量、概率分布，到条件概率，我们将逐步深入理解这些概念是如何与MSE紧密相连的。

## 2.1 随机变量和概率分布

### 2.1.1 随机变量的定义和分类
随机变量是指其取值具有不确定性的变量，通常用大写字母如 X、Y 表示。根据取值的性质，随机变量分为离散型和连续型两大类。

- **离散型随机变量**是指只能取有限个或可数无限多个值的随机变量，比如抛硬币的次数、掷骰子的点数等。例如，令 X 表示掷一次六面骰子的结果，则 X 是一个离散型随机变量，其可能的取值为 {1, 2, 3, 4, 5, 6}。

- **连续型随机变量**则可以取任意实数值，在一定的区间内取值是连续的，例如测量的温度、降雨量等。连续型随机变量通常通过概率密度函数（Probability Density Function, PDF）来描述。对于连续型随机变量，概率计算公式为 P(X=a) = 0，因为连续型随机变量取特定值的概率为零，但其取值落在某个区间内的概率不为零。

### 2.1.2 概率分布的基本概念
概率分布描述了一个随机变量所有可能取值的概率。对于离散型随机变量，我们使用概率质量函数（Probability Mass Function, PMF）来描述其概率分布；对于连续型随机变量，我们使用概率密度函数（PDF）来描述。此外，累积分布函数（Cumulative Distribution Function, CDF）是描述随机变量取值小于或等于某值的概率，是 PMF 或 PDF 的积分（连续型）或求和（离散型）。

概率分布的性质和形式对MSE有着直接的影响，MSE在计算期望损失时，依赖于随机变量的概率分布。在机器学习模型中，我们通过数据来估计这些分布，进而估计MSE。

## 2.2 常见的概率分布与MSE

### 2.2.1 高斯分布与MSE的数学推导
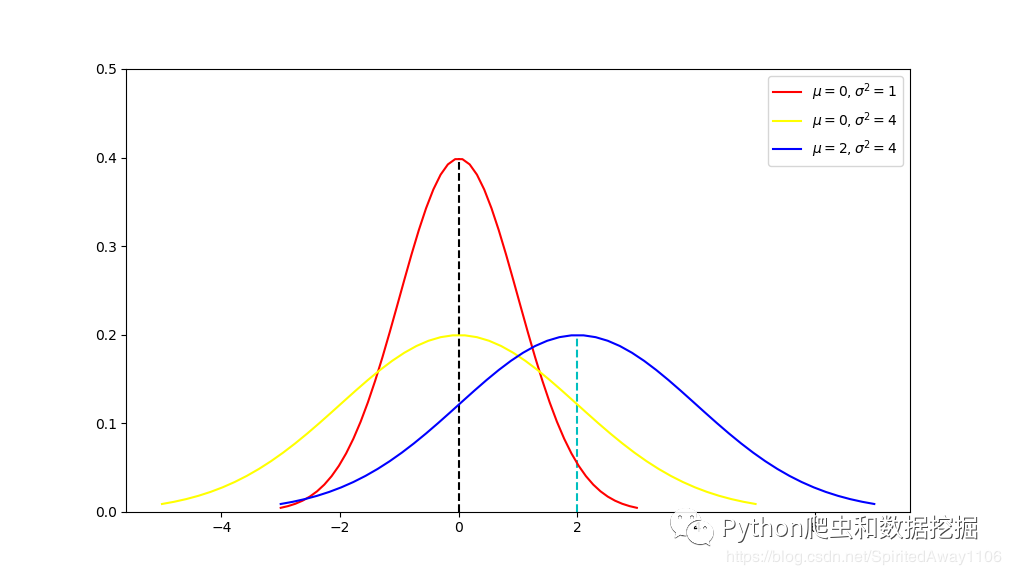
高斯分布，也称正态分布，是最常见的连续型概率分布之一。其概率密度函数为：

f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}

其中，μ 是均值，σ^2 是方差，分别决定分布的位置和宽度。在机器学习中，特别是在回归分析中，我们假设误差项呈高斯分布，并且基于最小化MSE来估计模型参数。

在高斯分布的假设下，MSE的数学推导表明，最小化MSE等价于最大似然估计（MLE）：

MSE(\theta) = E[(Y - f(X;\theta))^2] = \sigma^2 + (\mu - f(X;\theta))^2

当 f(X;θ) = μ 时，即模型预测值等于真实均值时，MSE达到最小值 σ^2。因此，最小化MSE与模型的均值拟合程度相关。

### 2.2.2 伯努利分布和二项分布对MSE的影响
**伯努利分布**描述了只有两种可能结果的随机实验，例如抛硬币（正面或反面）。其概率质量函数为：

f(x|p) = p^x(1-p)^{1-x}

其中，p 是成功（正面）的概率。

**二项分布**是伯努利分布的推广，描述了在 n 次独立的伯努利实验中成功的次数。其概率质量函数为：

f(k;n,p) = \binom{n}{k}p^k(1-p)^{n-k}

伯努利分布和二项分布在二元分类问题中非常常见，例如，在逻辑回归模型中，模型输出被解释为成功（正类）的概率，然后与一个阈值比较来分类。MSE 在这种情况下衡量的是模型预测概率与真实概率之间的差异。由于二项分布可以看作是多个独立的伯努利分布的和，因此其对MSE的影响更加显著。

## 2.3 条件概率与MSE的进一步探讨

### 2.3.1 条件概率的定义及其性质
条件概率是指在某一个事件已经发生的条件下，另一事件发生的概率。如果 A 和 B 是两个事件，那么条件概率 P(A|B) 定义为：

P(A|B) = \frac{P(A \cap B)}{P(B)}

只有当 P(B) > 0 时，条件概率才有定义。条件概率满足以下性质：

P(A_1 \cup A_2 | B) = P(A_1 | B) + P(A_2 | B) - P(A_1 \cap A_2 | B)

在机器学习中，条件概率是很多算法的基础，比如朴素贝叶斯分类器，以及在贝叶斯优化中MSE的更新也依赖于条件概率。

### 2.3.2 条件概率在MSE中的应用实例
条件概率在MSE计算中的一个应用实例是在线性回归模型中，当我们知道输入 X 的条件下，输出 Y 的分布是高斯分布时，最小化MSE可以得到模型参数的最佳线性无偏估计（BLUE）。这与高斯分布的条件概率密度函数紧密相关。

举一个简单例子，在一个二元回归模型中，我们的目标是最小化均方误差：

MSE = E[(Y - (β_0 + β_1X))^2 | X=x]

我们假设 Y | X = x 是均值为 β_0 + β_1x，方差为 σ^2 的正态随机变量。此时，我们可以利用条件概率分布来求解参数 β_0 和 β_1 的估计值。通过求解最小化条件期望的参数值，我们得到参数的BLUE。

在机器学习模型中，尽管我们