探索MATLAB智能算法在异常检测中的应用：揭秘异常检测算法的奥秘

# 1. 异常检测概述**

异常检测是一种识别数据集中偏离正常模式的异常值或异常事件的技术。它在各个领域至关重要，例如欺诈检测、网络安全和医疗诊断。异常检测算法通常基于机器学习模型，利用数据中的模式和关系来识别异常值。

异常检测算法可分为监督学习、无监督学习和半监督学习三种主要类型。监督学习算法需要标记的数据，而无监督学习算法则不需要。半监督学习算法使用少量标记数据和大量未标记数据进行训练。

# 2. MATLAB智能算法在异常检测中的理论基础

### 2.1 机器学习与异常检测

#### 2.1.1 异常检测的定义和类型

异常检测是一种识别与正常数据模式显著不同的数据点的过程。异常值可以是异常事件、异常行为或异常对象。异常检测在许多领域都有着广泛的应用，包括欺诈检测、网络安全和医疗诊断。

异常检测算法可以分为两大类：

- **监督学习算法：**需要标记的数据集进行训练。
- **无监督学习算法：**不需要标记的数据集，直接从数据中学习正常模式。

#### 2.1.2 机器学习在异常检测中的作用

机器学习算法在异常检测中扮演着至关重要的角色，原因如下：

- **自动化：**机器学习算法可以自动化异常检测过程，减少人工干预。
- **准确性：**机器学习算法可以学习复杂的模式，从而提高异常检测的准确性。
- **可扩展性：**机器学习算法可以处理大规模数据集，这对于异常检测至关重要。

### 2.2 智能算法在异常检测中的应用

#### 2.2.1 监督学习算法

监督学习算法通过学习标记的数据集来识别异常值。常用的监督学习算法包括：

- **支持向量机（SVM）：**将数据点映射到高维空间，并使用超平面将正常数据点与异常值分隔开来。
- **决策树：**根据数据点的特征构建一棵树状结构，并使用决策规则将正常数据点与异常值分隔开来。
- **随机森林：**由多个决策树组成，通过投票的方式对异常值进行分类。

#### 2.2.2 无监督学习算法

无监督学习算法不需要标记的数据集，直接从数据中学习正常模式。常用的无监督学习算法包括：

- **K-均值聚类：**将数据点聚类成多个组，异常值通常属于较小的簇。
- **局部异常因子（LOF）：**计算每个数据点的局部密度，异常值通常具有较低的局部密度。
- **孤立森林：**随机选择数据点的子集并构建隔离树，异常值通常位于隔离树的根部。

#### 2.2.3 半监督学习算法

半监督学习算法介于监督学习和无监督学习之间，使用少量标记的数据和大量未标记的数据进行训练。常用的半监督学习算法包括：

- **图半监督学习：**将数据点表示为图中的节点，并使用图论技术来识别异常值。
- **协同训练：**使用多个学习器，每个学习器使用不同的数据视图，并通过协作提高异常检测的准确性。
- **自训练：**使用无监督学习算法生成伪标签，并使用这些伪标签来训练监督学习算法。

# 3. MATLAB智能算法在异常检测中的实践应用

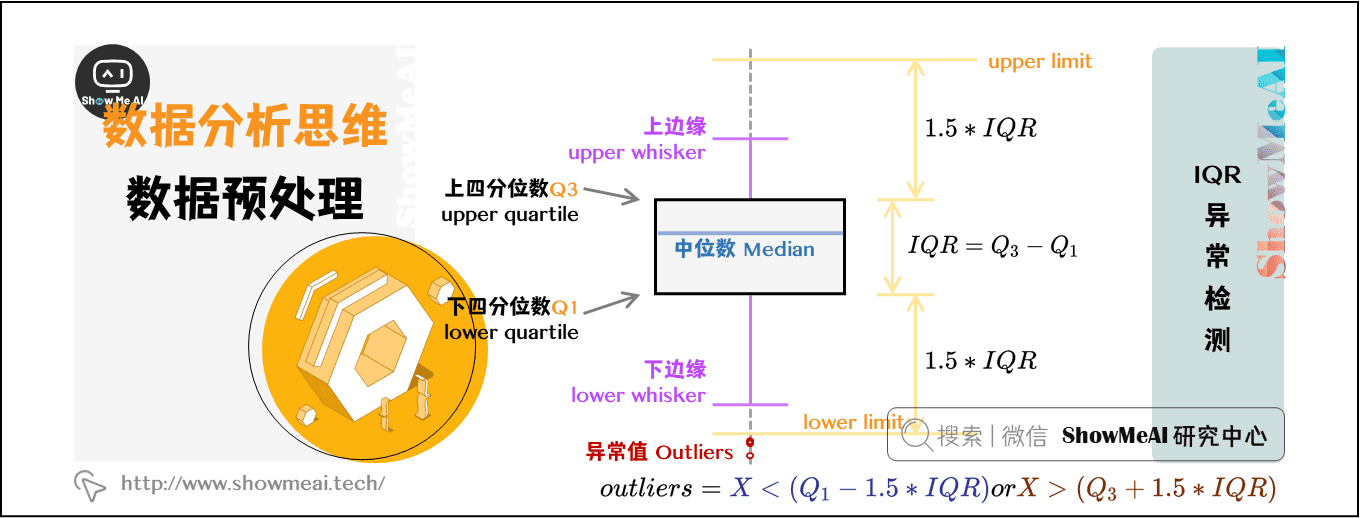
### 3.1 数据预处理与特征提取

#### 3.1.1 数据清理与缺失值处理

在异常检测中，数据预处理是至关重要的。数据预处理包括数据清理和缺失值处理。

数据清理涉及删除异常值、重复数据和噪声。异常值可以通过统计方法（如 z-score）或机器学习算法（如孤立森林）识别。重复数据可以通过哈希表或排序算法去除。噪声可以通过平滑技术（如移动平均）或降噪算法（如小波变换）去除。

缺失值处理涉及估计缺失值或删除包含缺失值的样本。缺失值估计可以通过插值（如线性插值或 k 最近邻）或机器学习算法（如回归模型）实现。删除包含缺失值的样本是一种简单的方法，但可能会导致信息丢失。

% 数据清理：删除异常值
data = data(abs(data - mean(data)) < 3 * std(data), :);

% 缺失值处理：线性插值
data(isnan(data)) = interp1(find(~isnan(data)), data(~isnan(data)), find(isnan(data)));

#### 3.1.2 特征工程与降维

特征工程是将原始数据转换为更适合异常检测的特征的过程。特征工程包括特征选择、特征提取和降维。

特征选择涉及选择与异常检测最相关的特征。特征选择可以通过过滤方法（如方差过滤或相关性分析）或包装方法（如递归特征消除或贪婪搜索）实现。

特征提取涉及创建新的特征，这些特征比原始特征更能表示异常。特征提取可以通过主成分分析（PCA）、奇异值分