精通MATLAB网络分析：进阶教程揭秘复杂网络模拟

# 1. MATLAB网络分析基础

## 1.1 网络分析的重要性
网络分析是研究复杂系统中元素间相互作用的基本工具。在MATLAB环境中，我们可以对各种网络系统进行深入分析，如社交网络、交通网络、生物网络等。借助MATLAB强大的数学计算和图形可视化能力，网络分析变得直观且高效。

## 1.2 MATLAB环境设置
开始网络分析前，确保你的MATLAB版本支持最新的网络分析工具箱。可以通过在MATLAB命令窗口输入`ver`命令来检查当前安装的工具箱。如果缺少网络分析工具箱，可以通过Matlab Add-On Explorer安装。

## 1.3 基本网络对象与操作
MATLAB中网络分析的基本单元是图（Graph）对象。创建一个简单的无向图可以通过`g = graph()`命令，然后使用`addedge()`函数增加边。例如：

g = graph();
g = addedge(g, 1, 2);  % 添加一条连接节点1和节点2的边

以上简单步骤为在MATLAB中进行网络分析打下了基础。第二章我们将深入探讨如何构建和操作复杂的网络模型。

# 2. MATLAB网络模型构建

## 2.1 网络图的基本概念与属性

### 2.1.1 图论在MATLAB中的实现

在MATLAB中实现图论，首先需要了解其基础概念。图是由节点（顶点）和边组成的抽象结构，用以描述元素间的关系。MATLAB提供了图论基础的函数和方法，用于构建和分析网络图。

% 创建一个简单的无向图
G = graph([1 1 1 2 2 3], [2 3 4 3 4 4]);

% 绘制图形
plot(G, 'EdgeLabel', G.Edges.Weight);

上面的代码创建了一个包含四个节点和六条边的无向图，其中`graph`函数用于构建图形，`plot`函数则用于绘制图形并显示边的权重。在MATLAB中，节点默认用整数编号，也可以通过`addnode`函数添加新的节点，通过`addedge`函数添加新的边。

图论的实现不仅限于构建和显示图形，还包含路径查找、图的遍历、连通性分析等复杂操作。MATLAB内置了多种算法来处理这些高级问题，例如`shortestpath`函数用于计算图中的最短路径。

### 2.1.2 网络的权重、方向性和连通性

在实际应用中，网络中的边可能带有关联的权重，表示连接的强度或成本；边也可能是有向的，表明关系的方向性；而连通性是指网络中所有节点是否相互可达。

% 定义边的权重
weights = [10 20 30 40 50 60];

% 创建带有权重的有向图
DG = digraph([1 1 1 2 2 3], [2 3 4 3 4 4], weights);

% 检查图的连通性
cond = condensation(DG);

在上述代码中，通过`digraph`函数创建了一个有向加权图，并通过`weights`数组为边赋予权重。`condensation`函数用于找出图的强连通分量，是分析连通性的常用方法。

这些属性对于描述现实世界中的各种网络至关重要。例如，在社交网络中，节点可以代表人，边可以代表人与人之间的联系，权重可以代表联系的亲密度，方向则表示交流的方向。

## 2.2 网络拓扑的MATLAB实现

### 2.2.1 创建不同类型网络拓扑

在网络建模中，不同类型的网络拓扑结构适用于不同的场景。MATLAB支持多种标准网络拓扑的生成，如规则网络、随机网络、小世界网络和无标度网络。

% 创建规则网络
RN = graph(bucky);

% 创建随机网络
RN = erdos_renyi_graph(20, 0.5);

% 创建小世界网络
SWN = watts_strogatz_graph(20, 4, 0.1);

% 创建无标度网络
BA = barabasi_albert_graph(20, 3);

上面的代码展示了如何在MATLAB中生成几种基本网络拓扑。`bucky`函数用于生成规则的网格网络，`erdos_renyi_graph`创建一个随机图，`watts_strogatz_graph`用于创建小世界网络模型，`barabasi_albert_graph`生成一个无标度网络模型。每种网络模型都有其特定的应用场景和特性。

### 2.2.2 随机网络、小世界网络与无标度网络的模拟

模拟网络拓扑是研究网络行为的重要手段。MATLAB提供丰富的函数库，用于模拟和分析这些网络结构的动态特性。

% 随机网络的连通组件分析
[components, num] = conncomp(RN);

% 小世界网络的聚类系数和平均路径长度计算
clustering_coefficient = clustering(RWN);
avg_path_length = mean_distance(SWN);

% 无标度网络的增长和优先连接模拟
BA = grow_network(20, 3);

在上述示例代码中，使用`conncomp`函数分析随机网络的连通组件，`clustering`和`mean_distance`函数分别计算小世界网络的聚类系数和平均路径长度，而`grow_network`函数模拟无标度网络的形成过程。通过这些模拟，研究人员能够了解不同网络拓扑的形成机制和演化规律。

## 2.3 网络数据的导入与分析

### 2.3.1 实际网络数据的导入方法

在研究和分析网络时，往往需要处理实际数据。MATLAB提供了多种工具来导入外部网络数据，如文本文件、表格或者专门的网络数据格式（如GraphML）。

% 从文本文件导入网络数据
fileID = fopen('network.txt', 'r');
data = textscan(fileID, '%d %d %f');
fclose(fileID);
G = graph(data{1}, data{2}, data{3});

% 从GraphML文件导入
G = readgraph('network.graphml');

上述代码展示了如何从文本文件和GraphML文件中导入网络数据。`textscan`函数可以解析文本文件中的网络数据，而`readgraph`函数直接读取GraphML格式的网络文件。通过这些方法，可以将外部数据整合到MATLAB环境中进行分析。

### 2.3.2 数据预处理与特征分析

网络数据往往需要预处理才能进行有效分析。预处理包括数据清洗、去噪和标准化等步骤。之后，可以通过多种方法进行特征分析，以提取网络的有用信息。

% 数据预处理示例
% 假设data已经加载到MATLAB中
data净 = remove_loops(data);
data净 = remove_self_loops(data净);
data净 = simplify(data净); % 合并多重边

% 特征分析示例
% 计算度分布
degrees = degrees(G);
figure; hist(degrees);
title('Degree Distribution');
xlabel('Degree');
ylabel('Number of Nodes');

在上述代码中，首先使用`remove_loops`和`remove_self_loops`函数去除图中的自环和重边，使用`simplify`函数合并多重边。接着，通过`degrees`函数计算网络中每个节点的度，并绘制度分布直方图。这些操作帮助理解网络结构的全局特性，并为进一步分析提供依据。

下一章将介绍如何应用MATLAB进行网络分析的算法应用。

# 3. MATLAB网络分析的算法应用

在深入探讨MATLAB网络分析的算法应用之前，需要了解算法基础、动态特性分析，以及如何将这些算法应用于网络问题的解决。本章将通过实际案例和深入解析，为读者提供一个全面的网络算法应用框架。

## 3.1 网络算法基础

### 3.1.1 最短路径算法

在网络中，找到两点之间最短路径是一个经典问题。MATLAB提供了多种图论算法，其中Dijkstra算法是解决加权无向图中单源最短路径问题的常用算法。

#### 实现Dijkstra算法的MATLAB代码示例：

function [dist, path] = dijkstra(graph, startNode)
    % graph: 邻接矩阵表示的图
    % startNode: 起始节点索引
    % dist: 路径长度
    % path: 最短路径节点序列

    numNodes = size(graph, 1);
    dist = inf(1, numNodes);
    prev = zeros(1, numNodes);
    dist(startNode) = 0;
    unvisited = 1:numNodes;

    while ~isempty(unvisited)
        [~, u] = min(dist(unvisited));
        u = unvisited(u);
        unvisited(u) = [];
        for v = unvisited
            if graph(u, v) > 0 && dist(u) + graph(u, v) < dist(v)
                dist(v) = dist(u) + graph(u, v);
                prev(v) = u;
            end
        end
    end

    % Reconstruct the shortest path from startNode to each node
    path = num2cell(NaN(1, numNodes));
    for i = 1:numNodes
        if ~isnan(prev(i))
            path{i} = i;
            while ~isnan(prev(path{i}(1)))
                path{i} = [prev(path{i}(1)), path{i}];
            end
        end
    end
end

#### 参数说明和逻辑分析：

- `graph`: 输入图的邻接矩阵，其中非零元素表示节点间的连接。
- `startNode`: 指定的起始节点。
- `dist`: 输出的从起始节点到各个节点的最短路径长度。
- `path`: 输出的从起始节点到各个节点的最短路径。

代码首先初始化距离数组`dist`和前驱节点数组`prev`。然后，进入一个循环，每次选择未访问节点中距离最小的节点进行处理，更新其它节点到起始节点的距离，并记录路径信息。

### 3.1.2 社区检测算法

社区检测是网络分析中的另一项重要任务，旨在发现网络中的密集连接区域。模块度优化算法是其中一种广泛应用的方法。

#### 社区检测算法的MATLAB伪代码示例：

function communities = communityDetection(graph)
    % graph: 邻接矩阵表示的图
    % communities: 节点所属的社区索引数组

    % 初始化社区分配，可以随机分配或使用启发式方法
    communities = randi(numNodes, 1, numNodes);
    % 迭代优化模块度
    improved = true;
    while improved
        improved = false;
        % 对于每对节点，尝试交换它们的社区分配
        for i = 1:numNodes, j = i+1:numNodes
            % 如果交换能提高模块度，执行交换
            if improveModularity(graph, i, j, communities)
                communities([i, j]) = communities([j, i]);
                improved = true;
            end
        end
    end
end

function improvement = improveModularity(graph, nodeI, nodeJ, communities)
    % 计算交换前后模块度的变化
    % ...
end

社区检测是一个迭代优化过程，其中模块度是评价社区划分好坏的重要指标。该伪代码展示了社区检测的基本思想，但是省略了模块度计算等细节，需要根据具体算法进行填充。

## 3.2 网络动态特性的MATLAB分析

### 3.2.1 网络演化模型

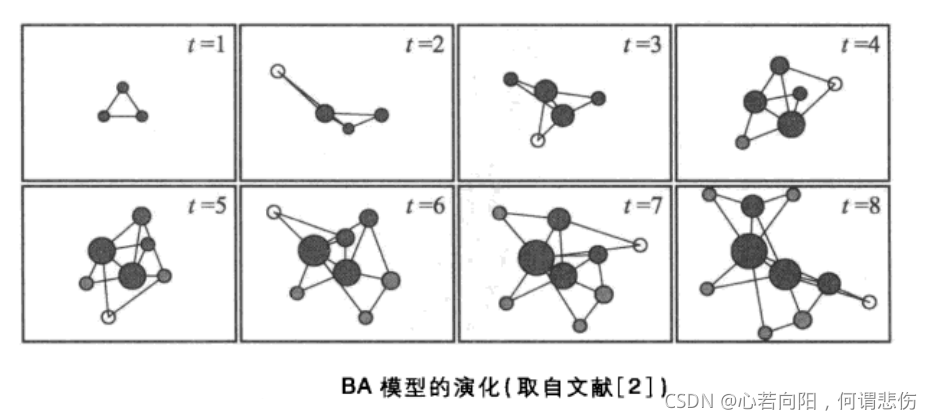
网络演化模型关注的是网络是如何随时间发展和变化的。这里以BA无标度网络演化模型为例进行说明。

#### BA模型的MATLAB伪代码示例：

function network = baModel(numNodes, numEdges)
    % numNodes: 网络最终节点数
    % numEdges: 初始边数
    % network: 生成的无标度网络

    % 初始化网络
    network = sparse(numNodes, numNodes);
    preferentialAttachment = randperm(numNodes, numEdges);
    % 生成初始网络
    for i = 1:numEdges
        network(preferentialAttachment(i), preferentialAttachment(i)) = 1;
    end
    for step = numEdges+1:numNodes
        % 随机选择一个新节点
        newNode = randi(step-1);
        % 计算新节点的连接概率
        degreeSum = sum(network(:, newNode));
        connectionProb = network(:, newNode) / degreeSum;
        % 按照概率选择连接节点
        connectedNode = rouletteWheelSelection(connectionProb);
        % 添加边
        network(newNode, connectedNode) = 1;
        network(connectedNode, newNode) = 1;
    end
end

function selectedNode = rouletteWheelSelection(probabilities)
    % 使用轮盘赌选择方法从概率分布中选择节点
    % ...
end

这段伪代码展示了BA模型的基本步骤，即通过优先连接机制逐渐增加新节点，形成具有无标度特性的网络。

## 3.3 高级网络算法实践

### 3.3.1 多层网络分析

多层网络是现代网络分析中的一个重要方向，它能够表示更加复杂的网络结构。

#### MATLAB实现多层网络分析的代码框架：

function multilayerNetworkAnalysis(layers, interLinks)
    % layers: 各层网络的邻接矩阵列表
    % interLinks: 层间连接的邻接矩阵
    % 执行多层网络分析

    % 分析多层网络的连通性
    % ...

    % 分析多层网络的鲁棒性
    % ...
end

该函数框架用于分析多层网络的基本结构和特性。实际应用中，应根据具体分析目标填充相应逻辑。

在第三章的内容中，我们了解了网络算法的基础和动态特性分析。从最短路径算法的MATLAB实现，到社区检测算法的策略框架，再到多层网络分析的初步探讨，本章逐步深化了网络分析的技术与方法，为读者提供了可以应用于实际问题的工具。在后续章节中，我们将进一步探索网络模拟与优化方法，以及在网络科学中如何利用MATLAB实现高级技巧和集成其他工具。

# 4. MATLAB网络模拟与优化

## 4.1 网络模拟的实现

### 4.1.1 建立网络模拟框架

网络模拟是理解复杂网络行为和特性的重要手段。MATLAB提供了一套强大的工具，可以用来构建和模拟网络的动态行为。建立网络模拟框架涉及多个步骤，从网络结构的初始化到模拟过程的实施，再到模拟结果的分析。

**初始化网络结构**：首先，必须定义网络的节点和边，以及相应的属性。在MATLAB中，可以使用`graph`或`digraph`函数创建无权或有权的图。以下是一个创建无权无向图的示例代码：

% 创建一个含有5个节点的无向图
nodes = {'A', 'B', 'C', 'D', 'E'};
G = graph(nodes);

% 添加边
G = addedge(G, [1 2], [2 3]);  % 节点A连接到节点B，节点B连接到节点C

**定义动态规则**：网络的模拟往往需要定义节点和边的动态行为，例如，节点的状态如何随时间改变，边的权重如何变化等。在MATLAB中，可以使用`setEdgeWeights`函数动态改变边的权重。

% 设置初始边权重
weights = [1, 1];  % 假设有两条边的初始权重为1
G.Edges.Weight = weights;

% 模拟边权重随时间的变化
for t = 1:10
    weights = weights + randn(size(weights));  % 模拟随机权重变化
    setEdgeWeights(G, weights);
    pause(1);  % 暂停1秒模拟权重变化过程
end

**执行模拟过程**：在定义了网络结构和动态规则之后，可以通过循环来模拟网络随时间的行为。

### 4.1.2 模拟结果的可视化

模拟结果的可视化是评估模拟效果的重要环节。MATLAB通过内置的绘图函数提供了多种可视化选项，可以直观地展示网络结构和动态变化过程。

**静态图形展示**：使用`plot`函数可以生成静态的图形展示。

% 绘制图G的静态展示
figure;
plot(G, 'Layout', 'force');
title('静态网络图形展示');

**动态变化过程展示**：使用`drawnow`函数可以实时绘制网络的变化过程。

% 动态展示边权重的变化过程
figure;
for t = 1:10
    weights = weights + randn(size(weights));
    setEdgeWeights(G, weights);
    drawnow;  % 立即更新图形窗口
    pause(0.1);  % 暂停一小段时间以便观察变化
end

## 4.2 网络优化问题的MATLAB求解

### 4.2.1 网络优化理论基础

网络优化是网络分析中的一个关键领域，它旨在找到最优的网络配置，以满足特定的设计和性能标准。MATLAB提供了求解优化问题的工具箱，如`optimtool`和`linprog`函数，这些工具可以帮助我们解决网络设计中的线性规划、整数规划等问题。

**线性规划问题**：线性规划是一种用于在一组线性不等式约束条件下，优化（最大化或最小化）线性目标函数的数学方法。MATLAB中的`linprog`函数能够求解线性规划问题。

% 定义目标函数、不等式约束和边界条件
f = [-1; -1];  % 目标函数系数
A = [1, 2; 3, 1];  % 不等式约束系数矩阵
b = [2; 3];  % 不等式约束边界值

% 设置变量的边界
lb = zeros(2, 1);  % 变量的下界
ub = [1.5; 2];  % 变量的上界

% 求解线性规划问题
[x, fval] = linprog(f, A, b, [], [], lb, ub);

% 输出最优解和最优值
disp('最优解：');
disp(x);
disp('最优目标函数值：');
disp(fval);

### 4.2.2 网络设计与资源优化实例

为了具体说明如何在MATLAB中进行网络设计和资源优化，下面以一个简单的网络流量优化问题为例。

**问题描述**：假设有四个节点组成的网络，需要为每条连接分配流量，目标是在满足所有节点需求的同时，最小化总流量成本。

**步骤一：建立目标函数和约束**：目标函数和约束条件的建立是解决优化问题的基础。

% 目标函数系数
f = [1; 2; 3; 4];  % 假设每条边的流量成本系数

% 不等式约束条件（网络流量需求）
A = [1, 0, 0, 0;
     1, 1, 0, 0;
     0, 1, 1, 0;
     0, 0, 1, 1;
     0, 0, 0, 1];
b = [100; 150; 120; 130; 100];  % 假设节点需求流量

% 边界条件
lb = zeros(4, 1);  % 流量的下限为0
ub = [Inf; Inf; Inf; Inf];  % 流量的上限为无穷大

% 求解
[x, fval] = linprog(f, A, b, [], [], lb, ub);

**步骤二：结果解读与应用**：求解得到的x向量即为每条边的最优流量分配，fval为目标函数的最优值，即最小化总成本。

## 4.3 案例研究：复杂网络模拟实战

### 4.3.1 选取行业案例进行网络分析

在这一部分，我们通过一个行业案例来展示如何使用MATLAB进行网络分析。假定我们要分析一个社交网络中信息传播的动态特性。我们会利用网络模拟技术，通过构建社交网络模型，来模拟信息如何在网络中传播。

**构建社交网络模型**：社交网络的构建首先需要收集数据，例如用户之间的交互关系。接下来，我们使用这些数据来创建网络模型。

% 假设我们有以下用户交互数据
% 用户对和交互次数
userInteractions = [
    'Alice' 'Bob'   10;
    'Alice' 'Charlie' 5;
    'Bob' 'Charlie' 8;
    'Bob' 'Diana' 6;
    'Charlie' 'Diana' 3;
    % ... 更多的交互数据
];

% 创建无向图
nodes = unique([userInteractions(:, 1) userInteractions(:, 2)]);
G = graph(userInteractions(:, 1), userInteractions(:, 2), userInteractions(:, 3), nodes);

**模拟信息传播**：在模拟信息传播时，我们通常需要定义信息的传播规则，例如，用户接收信息的概率等。

% 模拟信息传播
infectionRates = 0.8;  % 假定用户接收信息的概率为80%
nSteps = 50;  % 模拟50个时间步

for t = 1:nSteps
    for v = 1:nv(G)
        if rand < infectionRates
            % 这里定义接收到信息的节点的行为
            % 例如，可以将信息传播给相邻的节点
            neighbors = neighbors(G, v);
            % 随机选择一个邻居传播信息
            if ~isempty(neighbors)
                target = randi(length(neighbors));
                G = addedge(G, v, neighbors(target));
            end
        end
    end
    drawnow;  % 更新图形展示
end

### 4.3.2 分析结果的解读与应用

在执行了模拟后，我们可以得到信息传播的动态过程。分析这些结果可以帮助我们理解信息在网络中的传播模式，识别关键节点，预测可能的传播路径等。

**关键节点分析**：在网络传播中，有些节点可能扮演着更为重要的角色，比如中心节点或桥接节点。MATLAB的网络分析工具可以帮助我们识别这些节点。

% 计算度中心性
centrality = centrality(G, 'degree');

% 找到度中心性最高的节点，即为关键节点
[~, criticalNode] = max(centrality);
disp(['关键节点是: ', nodes{criticalNode}]);

**结果的应用**：利用这些分析结果，网络管理员可以制定更有效的信息传播策略，比如针对关键节点进行优先营销，或者优化网络结构以提高信息传播效率。

# 5. MATLAB在网络科学中的进阶技巧

## 5.1 高级图形用户界面(GUI)的设计

在进行复杂的网络分析时，一个直观且功能齐全的图形用户界面(GUI)可以大幅提升工作效率和用户体验。MATLAB提供了强大的工具箱来设计GUI，包括GUIDE和App Designer。我们可以按照以下步骤设计一个定制化的网络分析GUI。

### 5.1.1 设计定制化网络分析GUI

1. **启动GUIDE或App Designer**：通过MATLAB命令窗口输入`guide`或`appdesigner`启动设计界面。
2. **布局控件**：在GUIDE中，拖放按钮、文本框、图形显示等控件到工作区；在App Designer中，使用拖放编辑器添加所需的组件。
3. **设置控件属性**：为控件设置诸如名称、标签、大小、颜色等属性，以满足个性化需求。
4. **编写回调函数**：为每个控件的交互行为编写回调函数，实现图形绘制、分析功能等。
5. **测试GUI**：运行GUI应用，测试各项功能是否正常工作。

示例代码块展示一个简单的回调函数，该函数根据用户选择的网络分析类型，在GUI中显示相应的图形。

function button_nodeClicked(app, event)
    % 假设用户点击了显示节点信息的按钮
    nodeInfo = get(app.NodeInfoText, 'String'); % 获取节点信息字符串
    app.GraphDisplay.String = nodeInfo; % 在图形显示组件中显示节点信息
end

### 5.1.2 交互式网络模拟演示

设计GUI的关键之一是实现用户与网络模型之间的交互。例如，用户可以通过选择不同的参数来观察网络的动态变化。

1. **参数选择**：提供下拉菜单、滑动条等控件让用户选择或修改网络参数。
2. **模拟运行**：用户通过点击按钮触发网络模拟函数，该函数根据用户设定的参数进行计算，并在GUI中实时更新结果。
3. **结果展示**：模拟结果可以通过图形或表格的形式展示给用户。

以下是交互式网络模拟的代码片段：

function simulateButtonPushed(app, event)
    % 用户点击了模拟按钮后执行的回调函数
    parameters = app.Parameters; % 获取用户设置的参数
    [status, result] = simulateNetwork(app, parameters); % 执行模拟
    if status == 0
        app.GraphDisplay.String = displayResult(result); % 展示模拟结果
    else
        errorMessage = fprintf('模拟失败：错误代码 %d\n', result);
        app.ErrorDisplay.String = errorMessage; % 展示错误信息
    end
end

## 5.2 MATLAB与其他网络分析工具的集成

MATLAB除了自身强大的网络分析能力，还可以与Python等其他工具集成，扩大其应用范围。

### 5.2.1 集成Python网络分析工具

MATLAB和Python的集成可以通过MATLAB的Python接口或MEX接口来实现。通过这种方式，可以调用Python中的网络分析库，如NetworkX，以及利用Python进行数据分析的优势。

示例代码块展示如何在MATLAB中调用Python的NetworkX库。

% MATLAB调用Python代码的示例
python py
    import networkx as nx
    G = nx.erdos_renyi_graph(100, 0.05) % 创建一个随机图
    pos = nx.spring_layout(G) % 计算节点位置
    nx.draw(G, pos, with_labels=true)
end

### 5.2.2 利用MATLAB进行大数据网络分析

随着数据量的不断增大，传统的网络分析方法可能无法满足需求。MATLAB提供了分布式计算和内存映射数据等功能，可以对大规模网络数据进行分析。

1. **内存映射文件**：使用`memmapfile`函数处理超过内存大小的数据集。
2. **分布式计算**：使用`spmd`、`distributed`、`parfor`等并行计算命令对大数据集进行并行处理。
3. **矩阵操作优化**：利用稀疏矩阵和分布式数组优化存储和计算。

示例代码块展示如何使用内存映射文件处理大数据。

% 利用内存映射文件处理大规模网络数据
m = memmapfile('large_network_data.bin', 'Format', {'uint32', 'uint32'}, 'Offset', [0 4]);
% 假设数据是边的集合，每条边由两个32位无符号整数组成
source_nodes = m.Data(:,1);
target_nodes = m.Data(:,2);
% 创建稀疏矩阵表示网络
A = sparse(source_nodes, target_nodes, 1, n, n);

在下一章节，我们将深入探讨MATLAB在网络科学中的创新应用，并展望未来网络分析方法的发展趋势。