【C#数据保护高级技巧】：***中的加密与哈希技术深度剖析

# 1. C#数据保护概述

在当今数字化时代，数据安全已成为企业和个人的重中之重。对于IT专业人士来说，掌握数据保护的技术至关重要。C#作为一种功能强大的编程语言，在数据保护方面提供了广泛的支持。在本章中，我们将概述C#在数据保护方面的基础和重要性，并对后续章节中将详细探讨的加密技术、哈希技术以及安全实践给出概览。本章节旨在为读者提供一个框架，以便更好地理解随后章节中展开的复杂主题。

随着本章的结束，读者将获得对C#数据保护全面的理解，并准备好深入探索如何使用C#进行数据加密、数据完整性和身份验证等高级数据保护技术。让我们开始深入数据保护的世界，用知识和技术保护我们最珍贵的信息资产。

# 2. C#中的加密技术

## 2.1 对称加密算法的原理与实现

### 2.1.1 对称加密的原理

对称加密算法是加密和解密过程中使用同一个密钥的技术。这一类算法之所以称为“对称”，是因为数据的加密密钥和解密密钥相同。这种算法设计简单且计算效率高，因此在数据保护领域得到广泛应用。对称加密的典型应用场景包括文件加密、数据库加密和安全通信协议中的数据加密。

对称加密的主要组成部分包括：

- **加密算法**：用于将明文转换为密文的数学函数。
- **密钥**：控制加密算法行为的秘密参数，密钥的保密性决定了加密的安全性。
- **初始化向量(IV)**（可选）：某些算法为了增加加密的复杂度和安全性，使用随机数作为初始值。
- **模式**：加密模式定义了如何在多个数据块上应用加密算法，常见的模式包括ECB、CBC、CFB和OFB等。

### 2.1.2 实践：使用AES进行数据加密

高级加密标准（AES）是目前广泛使用的对称加密算法之一。AES以固定长度的块为单位处理数据，并支持128、192和256位三种密钥长度。

以下是一个使用C#进行AES加密和解密的简单示例：

using System;
using System.IO;
using System.Security.Cryptography;
using System.Text;

public class AesExample
{
    public static void EncryptDecryptAes(string plainText, string passPhrase)
    {
        // 密钥和IV将从密码生成
        byte[] saltStringBytes = Generate256BitsOfRandomEntropy();
        Rfc2898DeriveBytes password = new Rfc2898DeriveBytes(passPhrase, saltStringBytes, 1000);

        // 密钥的字节数组
        byte[] symmetricKey = password.GetBytes(32);
        // IV的字节数组
        byte[] iv = password.GetBytes(16);

        using (Aes encryptor = Aes.Create())
        {
            encryptor.Key = symmetricKey;
            encryptor.IV = iv;

            // 创建加密器和解密器流
            using (ICryptoTransform encryptorCryptoTransform = encryptor.CreateEncryptor())
            using (ICryptoTransform decryptorCryptoTransform = encryptor.CreateDecryptor())
            {
                using (var memoryStream = new MemoryStream())
                {
                    using (var cryptoStream = new CryptoStream(memoryStream, encryptorCryptoTransform, CryptoStreamMode.Write))
                    {
                        using (var streamWriter = new StreamWriter(cryptoStream))
                        {
                            streamWriter.Write(plainText);
                        }
                        // 加密数据的二进制表示
                        byte[] encrypted = memoryStream.ToArray();
                        // 打印加密后的文本
                        Console.WriteLine("encrypted.Text");
                        Console.WriteLine(ASCIIEncoding.ASCII.GetString(encrypted));
                    }

                    // 对加密数据进行解密
                    using (var memoryStream = new MemoryStream(encrypted))
                    {
                        using (var cryptoStream = new CryptoStream(memoryStream, decryptorCryptoTransform, CryptoStreamMode.Read))
                        {
                            using (var streamReader = new StreamReader(cryptoStream))
                            {
                                // 解密后的数据
                                string responseFromServer = streamReader.ReadToEnd();
                                Console.WriteLine("decrypted.Text");
                                Console.WriteLine(responseFromServer);
                            }
                        }
                    }
                }
            }
        }
    }

    private static byte[] Generate256BitsOfRandomEntropy()
    {
        var random = new byte[32]; // 32 bytes will give us 256 bits.
        using (var rngCsp = new RNGCryptoServiceProvider())
        {
            rngCsp.GetBytes(random);
        }
        return random;
    }
}

在此示例中，我们首先创建了一个随机的盐（salt）值和密钥，然后使用此密钥和初始化向量（IV）对文本数据进行加密。加密数据存储在`encrypted`字节数组中。之后，我们用相同的密钥和IV对加密数据进行解密，以验证解密是否能成功恢复原始文本。

## 2.2 非对称加密算法的原理与实现

### 2.2.1 非对称加密的原理

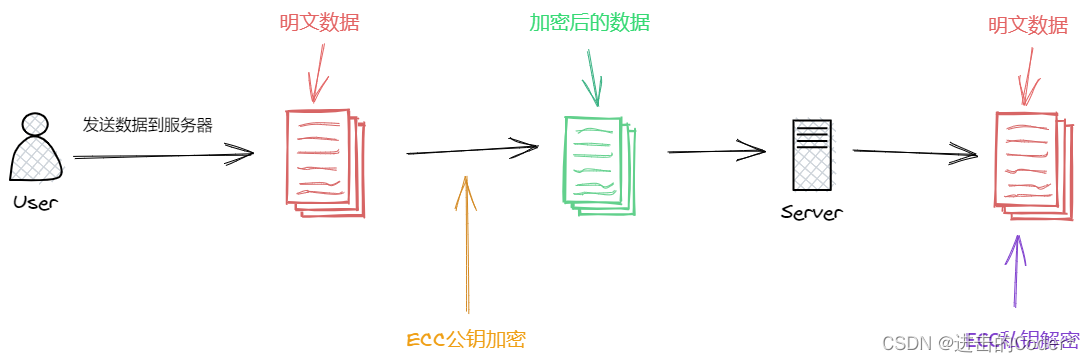
非对称加密是一种使用一对密钥——公钥和私钥的加密技术。公钥可以公开分享，用于加密信息；私钥必须保密，用于解密。这种技术也允许使用私钥对信息进行数字签名，以证明信息的来源和完整性。

非对称加密的两个典型算法是RSA和ECC（椭圆曲线加密）。RSA算法依赖于大数分解的难题，而ECC依赖于椭圆曲线的难题。由于非对称加密的数学基础和计算过程比对称加密复杂得多，因此非对称加密的速度较慢，通常用于密钥交换或数字签名，而不是直接用于大量数据的加密。

### 2.2.2 实践：使用RSA进行密钥交换

RSA算法在密钥交换过程中非常有用，因为它允许两个通信方在未共享私钥的情况下安全地交换对称加密的密钥。以下是一个简单的RSA密钥交换的C#实现示例：

using System;
using System.IO;
using System.Security.Cryptography;

public class RSAKeyExchangeExample
{
    public static void PerformKeyExchange()
    {
        // 创建两个RSA对象分别代表两方
        var rsaA = new RSACryptoServiceProvider();
        var rsaB = new RSACryptoServiceProvider();

        // 获取A方的公钥和私钥
        var parametersA = rsaA.ExportParameters(false);
        var publicA = rsaA.ToXmlString(false);

        // 获取B方的公钥和私钥
        var parametersB = rsaB.ExportParameters(false);
        var publicB = rsaB.ToXmlString(false);

        // A方使用B方的公钥加密信息
        var asymmetricKeyExchangeFormatter = new RSAPKCS1KeyExchangeFormatter(rsaA);
        byte[] message = Encoding.UTF8.GetBytes("The message to be securely transferred.");

        byte[] encryptedKeyData = asymmetricKeyExchangeFormatter.CreateKeyExchange(message, rsaB);

        // B方使用自己的私钥解密信息
        var asymmetricKeyExchangeDeformatter = new RSAPKCS1KeyExchangeDeformatter(rsaB);
        var decryptedMessage = asymmetricKeyExchangeDeformatter.DecryptKeyExchange(encryptedKeyData, rsaB);

        Console.WriteLine("Decrypted message:");
        Console.WriteLine(Encoding.UTF8.GetString(decryptedMessage));
    }
}

在此示例中，我们首先生成了两个RSA密钥对，然后使用一方的公钥加密信息。加密后的密钥数据随后发送给另一方，对方可以使用自己的私钥来解密信息。

请注意，实际应用中，非对称加密用于加密少量数据或用于密钥交换，而对称加密用于加密大量数据。这是因为非对称加密的开销更大，效率更低。

## 2.3 数字签名与身份验证