【编译原理高级话题】：DFA与其他自动机的深入关系探讨


# 摘要
确定性有限自动机（DFA）是一种基础的计算模型，在编译器设计、形式语言理论和算法实现中扮演着核心角色。本文详细探讨了DFA的基础理论与概念，通过与NFA、ε-NFA和PDA等其他自动机的比较分析，揭示了DFA的特有优势和应用限制。进一步，本文分析了DFA在编译器设计中的应用，尤其是在词法分析器的实现和性能优化方面。在现代理论探讨中，我们讨论了DFA的扩展和高级自动机模型，以及在形式语言理论中的地位。最后，本文介绍了DFA算法实现的最新工具支持，并对其在量子计算和工业界的应用前景进行了展望。

# 关键字
DFA；编译器设计；形式语言理论；算法实现；正则表达式；量子计算

参考资源链接：[DFA最小化算法实现及NFA到DFA转换](https://wenku.csdn.net/doc/3kcqsi0xiv?spm=1055.2635.3001.10343)
# 1. DFA的基础理论与概念

## 1.1 DFA的定义与组成
确定有限自动机（DFA）是一种抽象的数学模型，它由一组有限的状态、一个起始状态、一组接受状态以及一组状态转移规则组成。DFA能够对字符串进行识别，判断它们是否符合特定的模式。

## 1.2 DFA的工作原理
DFA的工作原理是基于状态转移。对于输入的每个符号，DFA根据当前状态和转移函数跳转到一个新的状态。如果在处理完所有的输入后，自动机处于接受状态，则输入字符串被认定为符合定义的语言。

## 1.3 DFA与正则表达式的关系
DFA和正则表达式紧密相关，实际上任何正则表达式都可以转换成DFA。正则表达式提供了字符串模式的文本描述，而DFA则以自动机的形式实现相同的模式识别功能。这一转换过程对于理解正则表达式的实际应用至关重要。

# 2. DFA与其他自动机的比较分析

### 2.1 DFA与NFA的对比

#### 2.1.1 构造差异与转换方法

确定性有限自动机（DFA）与非确定性有限自动机（NFA）是形式语言理论中两种重要的自动机模型。它们在识别正则语言方面具有等价的表达能力，但构造上存在显著差异。

DFA的特点是每个状态下对于每个输入符号都有唯一确定的转移，而NFA则允许在同一个状态下对一个输入符号有多个可能的转移，或者无转移。这种非确定性使得NFA的每个状态在接收到一个输入符号后，可以同时沿着多条路径前进，而DFA则需要严格按照确定的转移规则行进。

在转换方法上，将NFA转换成DFA的过程称为子集构造法（Subset Construction）。此方法需要将NFA的所有状态的可能组合视为DFA的候选状态，并计算出相应的转移规则。这通常导致DFA的状态数可能指数级增长于NFA的状态数。

示例代码展示如何使用Python实现NFA到DFA的转换：

# 示例中的伪代码
def nfa_to_dfa(nfa):
    dfa_states = set()
    dfa_transitions = {}
    # 初始化DFA状态集合和转移规则
    # ... 具体转换算法实现 ...
    return dfa_states, dfa_transitions

# 示例转换过程
nfa_states = {...}  # NFA的状态集合
nfa_transitions = {...}  # NFA的转移函数
initial_state = ...  # NFA的初始状态
accept_states = {...}  # NFA的接受状态集合

# 转换过程调用
dfa_states, dfa_transitions = nfa_to_dfa((nfa_states, nfa_transitions, initial_state, accept_states))

# 输出结果
print(dfa_states)
print(dfa_transitions)

#### 2.1.2 功能等价性与性能对比

尽管构造上的不同，DFA和NFA在功能上是等价的。这意味着对于任何NFA所识别的语言，都存在一个等价的DFA可以识别同样的语言。然而，这种等价性并不意味着它们在性能上没有差异。具体表现在：

1. **状态数量**：在转换过程中，DFA可能会产生大量的状态，尤其是在NFA有大量ε（空）转移的情况下。
2. **时间和空间复杂度**：构建DFA可能需要较长的时间，且占用更多的空间资源，因为状态数量可能大幅增长。
3. **实际应用**：DFA因其确定性，在实际的词法分析和模式匹配任务中，往往拥有更好的执行效率。

对于性能的对比，以下表格展示NFA与DFA在不同方面的性能对比：

| 特性 | NFA | DFA |
|------------|--------------|--------------|
| 状态数量 | 较少 | 较多 |
| 转移规则 | 可以存在多重 | 唯一确定 |
| 空间复杂度 | 较低 | 较高 |
| 时间复杂度 | 较快构建 | 执行效率高 |
| 实际应用 | 通常作为中间模型 | 适合实际匹配 |

### 2.2 DFA与ε-NFA的交互关系

#### 2.2.1 ε-NFA的定义与特性

ε-NFA（Epsilon-NFA）是NFA的一种扩展，它在自动机理论中增加了ε（空）转移的概念。ε转移允许自动机在没有读取任何输入符号的情况下从一个状态转移到另一个状态。ε-NFA使得自动机的表达能力更加强大，同时构造也更加灵活。

ε-NFA具有以下特性：

- **多重转移**：对于某些状态和输入符号，可以有多个目标状态。
- **空转移**：存在无需输入即可进行的状态转移。
- **接受状态**：可以有多个接受状态。

这些特性使得ε-NFA在理论上能够更加简洁地表示复杂的自动机结构。

#### 2.2.2 从ε-NFA到DFA的转换算法

ε-NFA到DFA的转换涉及到一个新的概念，即ε闭包（ε-closure）。ε闭包指的是从某个状态出发，通过一系列ε转移能够到达的所有状态的集合。以下是ε-NFA到DFA转换的主要步骤：

1. **计算ε闭包**：为每个状态计算ε闭包，找出所有可以通过ε转移到达的状态集合。
2. **状态转换**：构建新的DFA状态，每个状态对应于原始ε-NFA中的一个ε闭包。
3. **确定转移**：根据ε-NFA的转移规则，为DFA中每个状态定义对输入符号的转移。

示例代码展示如何使用Python实现ε-NFA到DFA的转换：

# 示例中的伪代码
def epsilon_nfa_to_dfa(epsilon_nfa):
    dfa_states = set()
    dfa_transitions = {}
    # 初始化DFA状态集合和转移规则
    # ... 具体转换算法实现 ...
    return dfa_states, dfa_transitions

# 示例转换过程
epsilon_nfa_states = {...}  # ε-NFA的状态集合
epsilon_nfa_transitions = {...}  # ε-NFA的转移函数
initial_state = ...  # ε-NFA的初始状态
accept_states = {...}  # ε-NFA的接受状态集合

# 转换过程调用
dfa_states, dfa_transitions = epsilon_nfa_to_dfa((epsilon_nfa_states, epsilon_nfa_transitions, initial_state, accept_states))

# 输出结果
print(dfa_states)
print(dfa_transitions)

### 2.3 DFA与PDA的互补性

#### 2.3.1 PDA的理论基础

下推自动机（Pushdown Automata，PDA）在自动机家族中占有特殊的位置，因为它可以识别上下文无关语言（Context-Free Language, CFL），而DFA仅能识别正则语言。PDA通过一个附加的栈结构来存储中间计算结果，从而使其具有处理递归结构的能力。

PDA与DFA在形式语言理论中有以下互补性质：

- **计算能力**：PDA能够识别DFA能识别的所有语言（即正则语言），并且能识别更广泛的语言。
- **结构差异**：PDA使用栈来存储信息，DFA使用固定的有限状态集合来存储信息。

#### 2.3.2 DFA与PDA在语言识别中的角色

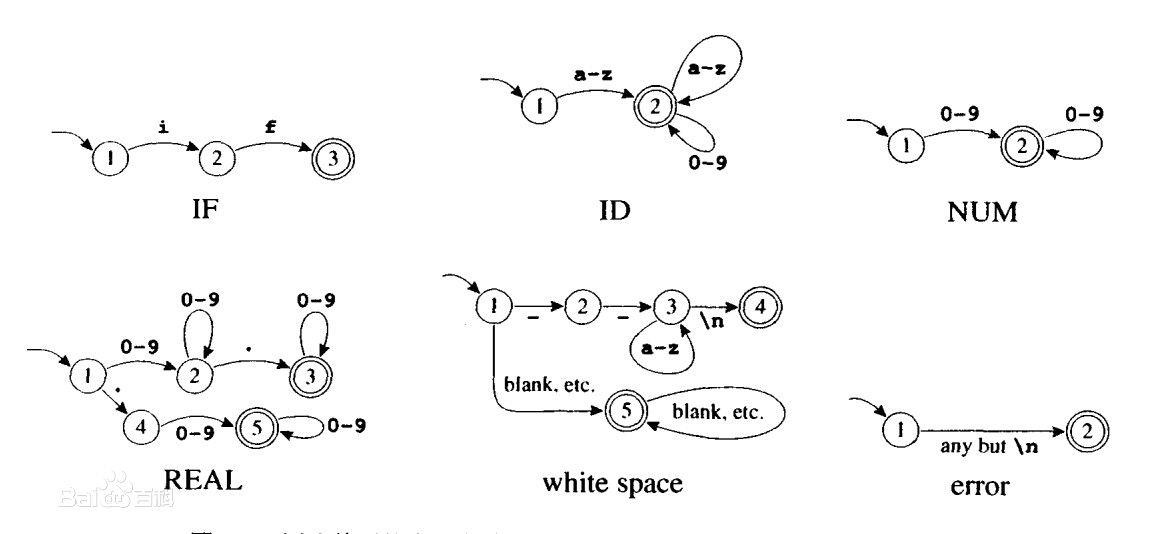
在编译器设计中，DFA和PDA分别扮演着不同的角色。DFA通常用于实现词法分析器，即识别源程序中的基本词法单元，如关键字、标识符、常数等。DFA的高效性使其在处理大量输入时具有优异的性能。

相比之下，PDA则用于语法分析阶段，即分析词法单元的语法结构，构建抽象语法树（AST）。由于词法分析和语法分析处理的语言特性不同，DFA和PDA在编译器设计中各自发挥着不可替代的作用。

接下来，在第三章中，我们将深入探讨DFA在编译器设计中的应用，包括实现词法分析器的具体方法和优化词法分析器性能的策略。

# 3. DFA在编译器设计中的应用

## 3.1 词法分析中的DFA实现
###