矩阵分解推荐系统：提升推荐准确率的秘籍，打造用户喜爱推荐

# 1. 矩阵分解推荐系统概述

矩阵分解推荐系统是一种基于矩阵分解技术构建的推荐系统，它通过将用户-物品交互矩阵分解成低秩矩阵，来捕捉用户偏好和物品特征之间的潜在关系。这种技术能够有效地解决传统推荐系统中存在的稀疏性和冷启动问题。

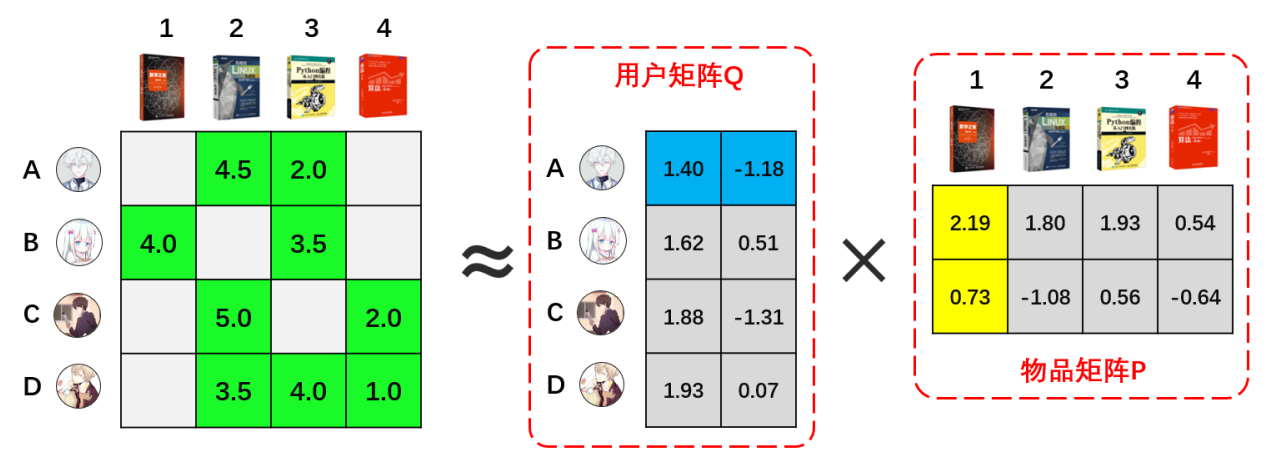
矩阵分解推荐系统的工作原理是：首先，将用户与物品之间的交互数据表示为一个用户-物品矩阵。然后，使用矩阵分解算法将该矩阵分解成两个低秩矩阵，其中一个矩阵表示用户潜在特征，另一个矩阵表示物品潜在特征。通过计算用户和物品潜在特征之间的相似度，即可生成推荐列表。

# 2. 矩阵分解推荐系统的理论基础

### 2.1 协同过滤与矩阵分解

协同过滤是一种推荐系统技术，它利用用户之间的相似性来预测用户对物品的偏好。在协同过滤中，用户-物品交互被表示为一个矩阵，其中行代表用户，列代表物品，单元格中的值表示用户对物品的评分或偏好。

矩阵分解是一种将用户-物品交互矩阵分解为两个较小矩阵的技术。一个矩阵代表用户潜在特征，另一个矩阵代表物品潜在特征。这些潜在特征捕获了用户偏好和物品属性的抽象表示。通过将用户和物品表示为潜在特征的线性组合，矩阵分解可以预测用户对未评分物品的偏好。

### 2.2 矩阵分解算法

有几种不同的矩阵分解算法，每种算法都有其独特的优势和劣势。

#### 2.2.1 奇异值分解（SVD）

奇异值分解（SVD）是一种广泛用于矩阵分解的算法。它将用户-物品交互矩阵分解为三个矩阵：

* **U：**一个行数等于用户数的矩阵，包含用户潜在特征。
* **Σ：**一个对角矩阵，包含奇异值。
* **V：**一个行数等于物品数的矩阵，包含物品潜在特征。

SVD 的优势在于它可以捕获用户和物品之间的线性关系。但是，它对于稀疏矩阵（即大多数单元格为零的矩阵）的性能不佳。

import numpy as np
from numpy.linalg import svd

# 用户-物品交互矩阵
R = np.array([[5, 3, 0, 1],
              [4, 0, 0, 1],
              [1, 1, 0, 5],
              [1, 0, 0, 4]])

# 奇异值分解
U, Σ, V = svd(R, full_matrices=False)

# 用户潜在特征
U_reduced = U[:, :2]

# 物品潜在特征
V_reduced = V[:, :2]

#### 2.2.2 非负矩阵分解（NMF）

非负矩阵分解（NMF）是一种将用户-物品交互矩阵分解为两个非负矩阵的算法：

* **W：**一个行数等于用户数的矩阵，包含用户潜在特征。
* **H：**一个行数等于物品数的矩阵，包含物品潜在特征。

NMF 的优势在于它可以捕获用户和物品之间的非线性关系。但是，它对于噪声数据敏感。

import numpy as np
from sklearn.decomposition import NMF

# 用户-物品交互矩阵
R = np.array([[5, 3, 0, 1],
              [4, 0, 0, 1],
              [1, 1, 0, 5],
              [1, 0, 0, 4]])

# 非负矩阵分解
model = NMF(n_components=2, init='random', random_state=0)
W = model.fit_transform(R)
H = model.components_

#### 2.2.3 张量分解（TD）

张量分解是一种将用户-物品交互张量分解为多个矩阵的算法。张量是一个三维或更高维的数据结构，它可以捕获用户、物品和时间或其他上下文信息之间的关系。

张量分解的优势在于它可以捕获用户和物品之间的高阶关系。但是，它计算成本高，对于大型数据集不切实际。

import numpy as np
import tensorflow as tf

# 用户-