【矩阵分解推荐系统：入门到精通，从零基础到高手进阶】

# 1. 矩阵分解推荐系统概述

矩阵分解推荐系统是一种基于矩阵分解技术构建的推荐系统。它将用户-物品交互数据表示为一个矩阵，并通过对该矩阵进行分解来学习用户和物品之间的潜在特征。这些特征可以用来预测用户对未交互物品的偏好，从而实现个性化推荐。

矩阵分解推荐系统具有以下优点：

- **可解释性强：**矩阵分解可以揭示用户和物品之间的潜在关系，便于理解推荐结果。
- **泛化能力好：**矩阵分解可以有效捕获用户偏好的变化，对稀疏数据和冷启动问题具有较好的鲁棒性。
- **可扩展性高：**矩阵分解算法可以并行化，适合大规模数据集的处理。

# 2. 矩阵分解推荐系统的理论基础

### 2.1 矩阵分解的原理和方法

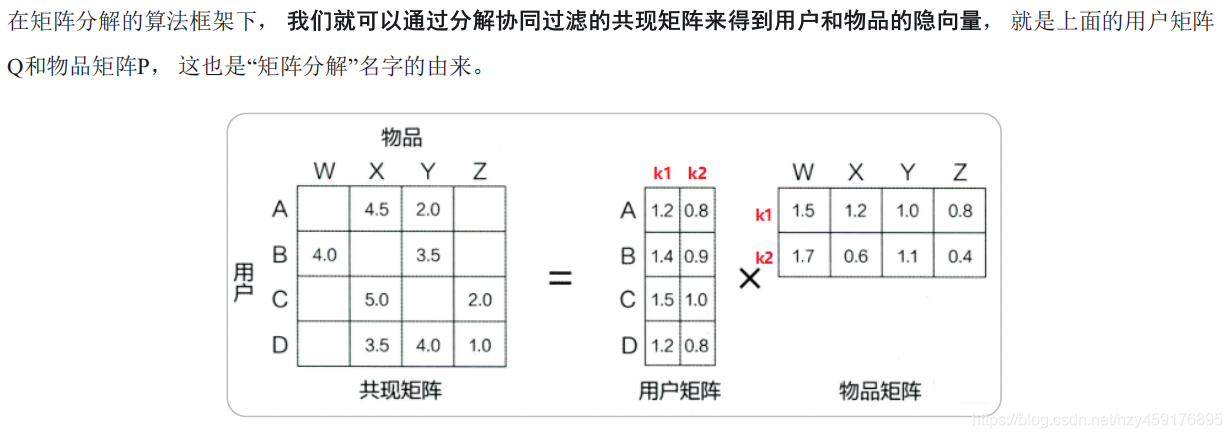
矩阵分解是一种将矩阵分解为多个较小矩阵的数学技术。在推荐系统中，矩阵分解用于将用户-物品交互矩阵分解为两个较小的矩阵：用户特征矩阵和物品特征矩阵。

#### 2.1.1 奇异值分解（SVD）

奇异值分解（SVD）是一种矩阵分解技术，它将矩阵分解为三个矩阵：

- 对角矩阵 U，包含矩阵的奇异值。
- 正交矩阵 V，包含矩阵的右奇异向量。
- 正交矩阵 W，包含矩阵的左奇异向量。

SVD 可以表示为：

A = UΣV^T

其中：

- A 是原始矩阵。
- U 是奇异值矩阵。
- Σ 是对角奇异值矩阵。
- V 是右奇异向量矩阵。
- W 是左奇异向量矩阵。

#### 2.1.2 非负矩阵分解（NMF）

非负矩阵分解（NMF）是一种矩阵分解技术，它将矩阵分解为两个非负矩阵：

- 用户特征矩阵 W。
- 物品特征矩阵 H。

NMF 可以表示为：

A = WH

其中：

- A 是原始矩阵。
- W 是用户特征矩阵。
- H 是物品特征矩阵。

### 2.2 推荐系统中的矩阵分解应用

矩阵分解在推荐系统中有多种应用，包括：

#### 2.2.1 协同过滤的矩阵分解方法

协同过滤是推荐系统中的一种流行方法，它利用用户之间的相似性来预测用户对物品的偏好。矩阵分解可以用于协同过滤，通过将用户-物品交互矩阵分解为用户特征矩阵和物品特征矩阵。

#### 2.2.2 内容推荐的矩阵分解方法

内容推荐是推荐系统中另一种流行的方法，它利用物品的属性来预测用户对物品的偏好。矩阵分解可以用于内容推荐，通过将物品-属性矩阵分解为物品特征矩阵和属性特征矩阵。

# 3. 矩阵分解推荐系统的实践实现

### 3.1 矩阵分解算法的选取和调参

#### 3.1.1 算法性能比较和选择

在实际应用中，根据不同的场景和数据特征，需要选择合适的矩阵分解算法。以下是一些常见的算法及其优缺点比较：

| 算法 | 优点 | 缺点 |
|---|---|---|
| 奇异值分解（SVD） | 精度高，可解释性强 | 计算复杂度高，不适用于稀疏矩阵 |
| 非负矩阵分解（NMF） | 可解释性强，适用于稀疏矩阵 | 精度可能较低 |
| 隐语义分析（LSA） | 可解释性强，适用于文本数据 | 精度可能较低 |
| 概率矩阵分解（PMF） | 适用于隐式反馈数据 | 计算复杂度高 |
| 协同过滤矩阵分解（CFMF） | 适用于协同过滤场景 | 计算复杂度高 |

#### 3.1.2 参数调优策略

矩阵分解算法通常涉及多个参数，需要通过调优来获得最佳性能。常用的调优策略包括：

- **网格搜索：**遍历参数的预定义范围，找到最优参数组合。
- **随机搜索：**在参数范围内随机采样，找到最优参数组合。
- **贝叶斯优化：**利用贝叶斯理论指导参数搜索，找到最优参数组合。

### 3.2 矩阵分解推荐系统的构建和部署

#### 3.2.1 数据预处理和模型训练

在构建矩阵分解推荐系统之前，需要对数据进行预处理，包括：

- **数据清洗：**去除缺失值、异常值和噪声数据。
- **数据标准化：**将数据缩放或归一化到统一的范围。
- **特征工程：**根据业务场景提取特征，丰富数据信息。

模型训练过程如下：

1. 选择合适的矩阵分解算法。
2. 设置算法参数。
3. 将预处理后的数据输入算法进行训练。
4. 根据评估指标评估模型性能。
5. 调整参数或选择不同的算法，优化模型性能。

#### 3.2.2 系统架构设计和部署

矩阵分解推荐系统通常采用以下架构：

graph LR
subgraph 数据层
    A[数据源]
    B[数据预处理]
    C[特征工程]
end
subgraph 模型层
    D[矩阵分解算法]
    E[模型训练]
    F[模型评估]
end
subgraph 服务层
    G[推荐服务]
    H[推荐接口]
end
subgraph 用户层
    I[用户交互]
end
A --> B
B --> C
C --> D
D --> E
E --> F
F --> G
G --> H
I --> G

系统部署过程如下：

1. 将训练好的模型部署到推荐服务。
2. 提供推荐接口供用户交互。
3. 监控系统性能，及时调整参数或优化模型。

# 4. 矩阵分解推荐系统的优化和扩展

### 4.1 矩阵分解推荐系统的性能优化

#### 4.1.1 算法并行化和加速

矩阵分解算法的计算量较大，尤其是在处理大型数据集时。为了提高计算效率，可以采用并行化和加速技术。

- **并行化：**将矩阵分解算法分解成多个独立的任务，并行地在多台机器或多核处理器上执行。常用的并行化技术包括分布式计算和多线程编程。
- **加速：**利用硬件加速器，如GPU或TPU，来执行矩阵分解算法。这些加速器具有大量的并行处理单元，可以显著提高计算速度。

**代码块：**

import numpy as np
from sklearn.decomposition import TruncatedSVD

# 并行化矩阵分解
svd = TruncatedSVD(n_components=100, n_iter=10, random_state=42)
svd.fit(X)

**逻辑分析：**

此代码块使用 scikit-learn 库中的 TruncatedSVD 类执行矩阵分解。`n_components` 参数指定分解后的矩阵秩，`n_iter` 参数指定迭代次数，`random_state` 参数指定随机数种子。通过调用 `fit` 方法，算法并行地执行矩阵分解，并返回分解后的矩阵。

#### 4.1.2 模型压缩和存储优化

矩阵分解模型通常会产生较大的存储空间需求。为了优化存储，可以采用模型压缩技术。

- **模型量化：**将模型参数从浮点数量化为低精度格式，如 int8 或 int16。这可以显著减少模型大小，而对准确性影响较小。
- **模型剪枝：**移除模型中不重要的参数。这可以进一步减少模型大小，同时保持模型的性能。

**代码块：**

import tensorflow as tf

# 模型量化
model = tf.keras.models.load_model('model.h5')
quantized_model = tf.keras.models.quantize_model(model)
quantized_model.save('quantized_model.h5')

**逻辑分析：**

此代码块使用 TensorFlow 库中的 `quantize_model` 函数对 Keras 模型进行量化。量化后的模型 `quantized_model` 具有更小的文件大小，同时保持与原始模型相似的性能。

### 4.2 矩阵分解推荐系统的扩展应用

矩阵分解推荐系统可以扩展到各种应用场景，以满足不同的业务需求。

#### 4.2.1 多模态推荐

多模态推荐系统利用来自不同模态（如文本、图像、音频）的数据来增强推荐效果。矩阵分解可以用于融合不同模态的数据，并生成更准确的推荐。

**流程图：**

graph LR
subgraph 多模态推荐系统
    A[文本数据] --> B[矩阵分解]
    C[图像数据] --> D[矩阵分解]
    E[音频数据] --> F[矩阵分解]
    B --> G[融合]
    D --> G
    F --> G
    G --> H[推荐结果]
end

**表格：**

| 模态 | 矩阵分解方法 |
|---|---|
| 文本 | 奇异值分解（SVD） |
| 图像 | 非负矩阵分解（NMF） |
| 音频 | 潜在狄利克雷分配（LDA） |

#### 4.2.2 时序推荐

时序推荐系统考虑了用户行为的时间序列信息，以生成更个性化的推荐。矩阵分解可以用于捕获用户行为随时间的变化，并生成时序推荐。

**代码块：**

import pandas as pd
from surprise import SVD

# 加载用户行为数据
data = pd.read_csv('user_behavior.csv')

# 构建时序推荐系统
model = SVD(n_factors=100, n_epochs=10, random_state=42)
model.fit(data)

**逻辑分析：**

此代码块使用 Surprise 库中的 SVD 算法构建时序推荐系统。`n_factors` 参数指定分解后的矩阵秩，`n_epochs` 参数指定迭代次数，`random_state` 参数指定随机数种子。通过调用 `fit` 方法，算法拟合用户行为数据，并学习用户行为随时间的变化模式。

# 5. 矩阵分解推荐系统的应用案例和前沿研究

### 5.1 矩阵分解推荐系统在不同领域的应用

矩阵分解推荐系统已广泛应用于各种领域，包括：

- **电商推荐：**亚马逊、阿里巴巴等电商平台使用矩阵分解推荐系统为用户推荐个性化的产品。
- **新闻推荐：**今日头条、Google News等新闻平台使用矩阵分解推荐系统为用户推荐感兴趣的新闻。
- **视频推荐：**YouTube、Netflix等视频平台使用矩阵分解推荐系统为用户推荐感兴趣的视频。
- **音乐推荐：**Spotify、Apple Music等音乐平台使用矩阵分解推荐系统为用户推荐个性化的音乐。
- **社交推荐：**Facebook、Twitter等社交平台使用矩阵分解推荐系统为用户推荐好友或感兴趣的内容。

### 5.2 矩阵分解推荐系统的最新研究进展

矩阵分解推荐系统是一个活跃的研究领域，近年来取得了显著进展，包括：

- **深度矩阵分解：**将深度学习技术融入矩阵分解模型，提高推荐的准确性和鲁棒性。
- **图神经网络与矩阵分解：**将图神经网络与矩阵分解相结合，利用图结构信息增强推荐效果。
- **可解释矩阵分解：**开发可解释的矩阵分解模型，便于理解推荐结果背后的原因。
- **隐私保护矩阵分解：**设计隐私保护的矩阵分解算法，保护用户隐私。
- **实时矩阵分解：**开发实时矩阵分解算法，应对动态变化的用户偏好和内容。