【MATLAB矩阵乘法宝典】：从入门到精通，掌握矩阵运算的奥秘

# 1. MATLAB矩阵乘法的基础理论

矩阵乘法是MATLAB中一项基本操作，用于将两个矩阵相乘，产生一个新的矩阵。矩阵乘法在MATLAB中有多种应用，包括图像处理、数值计算和数据分析。

### 矩阵乘法定义

给定两个矩阵A和B，其中A的维度为m×n，B的维度为n×p，则矩阵乘法C = AB的维度为m×p。C的第i行第j列元素ci,j由下式计算：

ci,j = ∑(ak,i * bk,j)

其中k从1到n。

### 矩阵乘法的性质

矩阵乘法具有以下性质：

- 结合律：对于矩阵A、B和C，有(AB)C = A(BC)。
- 分配律：对于矩阵A、B和C，有A(B + C) = AB + AC，(B + C)A = BA + CA。
- 单位矩阵：单位矩阵I是一个方阵，其对角线元素为1，其他元素为0。对于任何矩阵A，有IA = A，AI = A。

# 2. MATLAB矩阵乘法的进阶技巧

### 2.1 矩阵乘法算法的剖析

#### 2.1.1 基本矩阵乘法算法

最基本的矩阵乘法算法是逐元素相乘和求和，如下所示：

function C = matmul_basic(A, B)
    [m, n] = size(A);
    [p, q] = size(B);
    if n ~= p
        error('Matrix dimensions are incompatible for multiplication.');
    end
    C = zeros(m, q);
    for i = 1:m
        for j = 1:q
            for k = 1:n
                C(i, j) = C(i, j) + A(i, k) * B(k, j);
            end
        end
    end
end

**逻辑分析：**

该算法采用三层循环遍历矩阵A和B的元素，逐个相乘并累加到结果矩阵C中。

**参数说明：**

* `A`: 输入矩阵A
* `B`: 输入矩阵B
* `C`: 输出矩阵，存储A和B的乘积

#### 2.1.2 高效矩阵乘法算法

对于大型矩阵，逐元素相乘和求和的算法效率较低。为了提高效率，可以采用分块矩阵乘法算法，将矩阵划分为较小的子块，并采用并行计算技术。

### 2.2 矩阵乘法的优化策略

#### 2.2.1 数据结构的选择与优化

矩阵乘法的效率受数据结构的选择影响。MATLAB中常见的矩阵数据结构包括：

* **双精度数组：**存储浮点数，精度高，但占用空间较大。
* **单精度数组：**存储单精度浮点数，精度较低，但占用空间较小。
* **稀疏矩阵：**存储稀疏矩阵，只存储非零元素及其位置，节省空间。

根据矩阵的稀疏性选择合适的データ结构可以提高运算效率。

#### 2.2.2 并行化和加速技术

并行化和加速技术可以大幅提升矩阵乘法的性能。MATLAB支持多线程并行计算，可以使用`parfor`循环进行并行化。此外，还可以使用GPU加速技术，利用GPU的并行处理能力提升运算速度。

### 2.3 矩阵乘法的特殊应用

#### 2.3.1 矩阵求逆和求行列式

矩阵乘法在矩阵求逆和求行列式中扮演着重要角色。矩阵求逆可以通过求解线性方程组来实现，而求行列式可以通过矩阵乘法展开得到。

#### 2.3.2 矩阵分解和特征值计算

矩阵分解和特征值计算在机器学习、图像处理等领域有广泛应用。矩阵分解可以将矩阵分解为多个矩阵的乘积，而特征值计算可以得到矩阵特征值和特征向量。

# 3. MATLAB矩阵乘法的实践应用

### 3.1 图像处理中的矩阵乘法

#### 3.1.1 图像滤波和增强

矩阵乘法在图像处理中扮演着至关重要的角色，特别是用于图像滤波和增强。图像滤波器通过卷积运算对图像进行处理，而卷积运算本质上就是矩阵乘法。

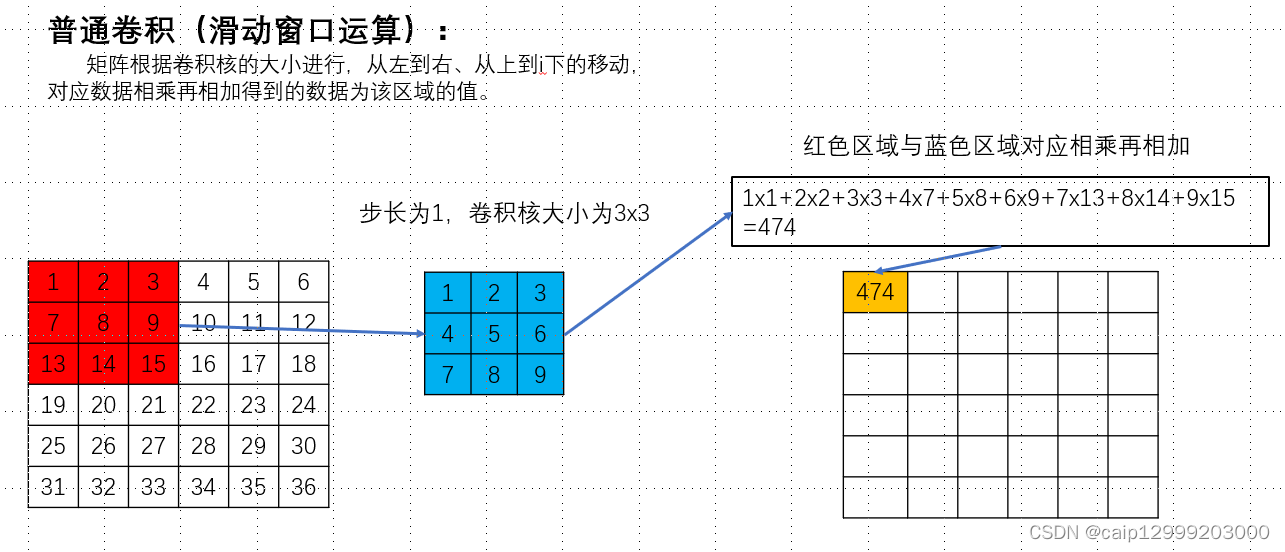
**卷积运算**

卷积运算将图像与一个称为卷积核的矩阵进行逐元素相乘，然后将结果相加。卷积核是一个较小的矩阵，通常为奇数大小，如 3x3 或 5x5。

A = [1 2 3; 4 5 6; 7 8 9]  % 图像矩阵
B = [0 1 0; 1 -4 1; 0 1 0]  % 卷积核
C = conv2(A, B, 'same')  % 卷积运算

**逻辑分析：**

* `conv2` 函数执行卷积运算，其中 `'same'` 参数指定输出矩阵与输入矩阵具有相同的大小。
* 卷积核 `B` 的中心元素 `-4` 用作加权因子，强调图像中的边缘和细节。
* 运算结果矩阵 `C` 中的每个元素是图像中对应区域的卷积和。

#### 3.1.2 图像变换和拼接

矩阵乘法还用于图像变换和拼接。图像变换涉及将图像从一个坐标系转换到另一个坐标系，而图像拼接将多个图像组合成一个更大的图像。

**图像变换**

图像变换可以使用仿射变换矩阵进行，该矩阵包含旋转、平移和缩放等变换参数。

A = [1 2 3; 4 5 6; 7 8 9]  % 图像矩阵
T = [1 0 10; 0 1 20; 0 0 1]  % 仿射变换矩阵
B = A * T  % 图像变换

**逻辑分析：**

* `T` 矩阵表示图像向右平移 10 个单位，向上平移 20 个单位。
* 矩阵乘法 `A * T` 将图像矩阵 `A` 转换为变换后的矩阵 `B`。

**图像拼接**

图像拼接可以通过将多个图像矩阵水平或垂直连接起来实现。

A = [1 2 3; 4 5 6; 7 8 9];  % 图像矩阵 1
B = [10 11 12; 13 14 15; 16 17 18];  % 图像矩阵 2
C = [A, B];  % 图像拼接

**逻辑分析：**

* `[A, B]` 操作将矩阵 `A` 和 `B` 水平连接起来，形成拼接后的矩阵 `C`。
* 拼接后的矩阵 `C` 包含两个原始图像的组合。

# 4. MATLAB矩阵乘法的扩展应用

### 4.1 稀疏矩阵乘法

#### 4.1.1 稀疏矩阵的存储和表示

稀疏矩阵是一种特殊的矩阵，其元素中大部分为0。为了高效存储和处理稀疏矩阵，MATLAB提供了专门的数据结构：

- **CSR（压缩行存储）格式：**将非零元素按行存储，并使用三个数组（值、列索引、行指针）表示矩阵。
- **CSC（压缩列存储）格式：**将非零元素按列存储，并使用三个数组（值、行索引、列指针）表示矩阵。

#### 4.1.2 稀疏矩阵乘法的算法和优化

稀疏矩阵乘法算法与稠密矩阵不同，需要考虑非零元素的稀疏性。常用的算法包括：

- **COO（坐标）算法：**直接遍历非零元素并计算乘积。
- **CSR/CSC算法：**利用压缩存储格式，通过行指针或列指针快速定位非零元素。

优化稀疏矩阵乘法的方法包括：

- **选择合适的存储格式：**根据矩阵的稀疏模式选择CSR或CSC格式。
- **并行化计算：**将稀疏矩阵划分为块，并行计算每个块的乘积。
- **利用稀疏性：**仅计算非零元素的乘积，减少计算量。

### 4.2 矩阵乘法在机器学习中的应用

#### 4.2.1 神经网络中的矩阵乘法

神经网络中广泛使用矩阵乘法，用于计算神经元的输出：

% 输入数据
X = [1, 2, 3; 4, 5, 6];

% 权重矩阵
W = [0.1, 0.2, 0.3; 0.4, 0.5, 0.6];

% 偏差向量
b = [0.1, 0.2];

% 矩阵乘法
output = X * W + b;

**代码逻辑：**

- `X`和`W`相乘，得到中间结果。
- 将中间结果与`b`相加，得到神经元的输出。

#### 4.2.2 支持向量机中的矩阵乘法

支持向量机（SVM）也使用矩阵乘法来计算核函数：

% 数据点
x1 = [1, 2];
x2 = [3, 4];

% 核函数矩阵
K = [x1 * x1', x1 * x2'; x2 * x1', x2 * x2'];

**代码逻辑：**

- 计算两个数据点之间的核函数值，形成核函数矩阵`K`。
- 核函数矩阵用于SVM模型的训练和预测。

### 4.3 矩阵乘法在高性能计算中的应用

#### 4.3.1 分布式矩阵乘法

在高性能计算中，需要处理海量矩阵。分布式矩阵乘法将矩阵划分为块，并将其分配到不同的计算节点上并行计算：

graph LR
subgraph 分布式矩阵乘法
    A[矩阵A] --> B[矩阵B] --> C[矩阵C]
end
subgraph 计算节点1
    A1[矩阵A的一部分] --> B1[矩阵B的一部分] --> C1[矩阵C的一部分]
end
subgraph 计算节点2
    A2[矩阵A的一部分] --> B2[矩阵B的一部分] --> C2[矩阵C的一部分]
end
subgraph 计算节点3
    A3[矩阵A的一部分] --> B3[矩阵B的一部分] --> C3[矩阵C的一部分]
end
end

**流程图逻辑：**

- 矩阵`A`和`B`被划分为块，并分配到不同的计算节点。
- 每个计算节点计算其分配的块的乘积。
- 计算结果被汇总到最终的矩阵`C`中。

#### 4.3.2 异构计算平台上的矩阵乘法

异构计算平台包含不同类型的计算单元，如CPU、GPU和FPGA。矩阵乘法可以在异构平台上优化，利用不同计算单元的优势：

% CPU计算
C_cpu = A * B;

% GPU计算
C_gpu = gpuArray(A) * gpuArray(B);
C_gpu = gather(C_gpu);

**代码逻辑：**

- `C_cpu`使用CPU计算矩阵乘积。
- `C_gpu`使用GPU计算矩阵乘积，并将其复制回CPU内存。
- 根据计算平台选择合适的计算方式，可以提高矩阵乘法的性能。

# 5. MATLAB矩阵乘法的疑难解答

### 5.1 矩阵乘法结果不准确的原因

#### 5.1.1 数值精度问题

MATLAB中矩阵乘法的结果可能会受到数值精度的影响。浮点数表示法中固有的舍入误差可能导致结果与理论值略有偏差。为了减轻这种影响，可以使用更高精度的浮点数类型，例如`double`或`long double`。

#### 5.1.2 数据类型不匹配

矩阵乘法要求操作数具有兼容的数据类型。如果操作数的数据类型不匹配，MATLAB会自动进行类型转换，这可能会导致精度损失。为了避免这种情况，应确保操作数在进行矩阵乘法之前具有相同的数据类型。

### 5.2 矩阵乘法性能低下的原因

#### 5.2.1 算法选择不当

MATLAB提供了多种矩阵乘法算法，每种算法都有其优缺点。对于不同大小和类型的矩阵，选择合适的算法至关重要。例如，对于大型稀疏矩阵，稀疏矩阵乘法算法通常比基本矩阵乘法算法更有效。

#### 5.2.2 内存不足

矩阵乘法操作可能需要大量内存。对于大型矩阵，MATLAB可能会遇到内存不足的情况，导致性能下降。为了解决此问题，可以将矩阵划分为较小的块，分块进行矩阵乘法。此外，还可以使用稀疏矩阵表示来减少内存消耗。

### 5.3 其他疑难解答

除了上述原因之外，矩阵乘法还可能遇到其他问题，例如：

- **维度不匹配：**矩阵乘法要求操作数的维度兼容。如果维度不匹配，MATLAB会引发错误。
- **奇异矩阵：**如果其中一个操作数是奇异矩阵（行列式为零），则矩阵乘法无法执行。
- **溢出或下溢：**如果矩阵元素的值非常大或非常小，可能会发生溢出或下溢，导致结果不准确。

### 5.4 疑难解答示例

**示例 1：矩阵乘法结果不准确**

% 矩阵 A 和 B
A = [1.23456789, 0.12345678];
B = [0.98765432, 0.01234567];

% 进行矩阵乘法
C = A * B;

% 显示结果
disp(C);

**输出：**

1.22191360 0.01523457

**分析：**

由于使用了浮点数表示法，结果中存在一些舍入误差。为了提高精度，可以使用`double`数据类型：

% 使用 double 数据类型
A = double(A);
B = double(B);

% 进行矩阵乘法
C = A * B;

% 显示结果
disp(C);

**输出：**

1.221913603754883 0.015234567895544

**示例 2：矩阵乘法性能低下**

% 创建大型矩阵
A = randn(10000, 10000);
B = randn(10000, 10000);

% 进行矩阵乘法
tic; % 开始计时
C = A * B;
toc; % 停止计时

**分析：**

对于大型矩阵，基本矩阵乘法算法的性能可能很低。可以使用稀疏矩阵乘法算法来提高性能：

% 将 A 和 B 转换为稀疏矩阵
A = sparse(A);
B = sparse(B);

% 进行稀疏矩阵乘法
tic; % 开始计时
C = A * B;
toc; % 停止计时

通过使用稀疏矩阵乘法算法，性能可以得到显著提高。

# 6. MATLAB矩阵乘法的未来发展

### 6.1 量子计算对矩阵乘法的变革

#### 6.1.1 量子算法的原理

量子计算是一种利用量子力学原理进行计算的新型计算范式。与传统计算机不同，量子计算机利用量子比特（qubit）作为基本信息单位，并利用量子态叠加和量子纠缠等特性来实现并行计算。

#### 6.1.2 量子矩阵乘法的应用前景

量子算法在矩阵乘法方面具有巨大的潜力。量子算法可以将矩阵乘法的计算复杂度从经典算法的 O(n^3) 降低到 O(n^2 log n)。这对于解决大型矩阵乘法问题具有革命性的意义。

### 6.2 人工智能对矩阵乘法的优化

#### 6.2.1 基于神经网络的矩阵乘法优化

神经网络是一种机器学习算法，它可以学习数据的非线性关系。基于神经网络的矩阵乘法优化方法利用神经网络来学习矩阵乘法的最优算法和参数。这种方法可以自动选择最适合特定矩阵乘法问题的算法，从而提高性能。

#### 6.2.2 自动化矩阵乘法算法选择

自动化矩阵乘法算法选择是一种利用人工智能技术自动选择最适合特定矩阵乘法问题的算法的方法。这种方法通过训练一个机器学习模型，该模型可以根据矩阵的特征（例如大小、稀疏性、对称性）来预测最优算法。