MATLAB矩阵乘法在机器人技术中的应用：赋能智能机器人，探索机器人奥秘

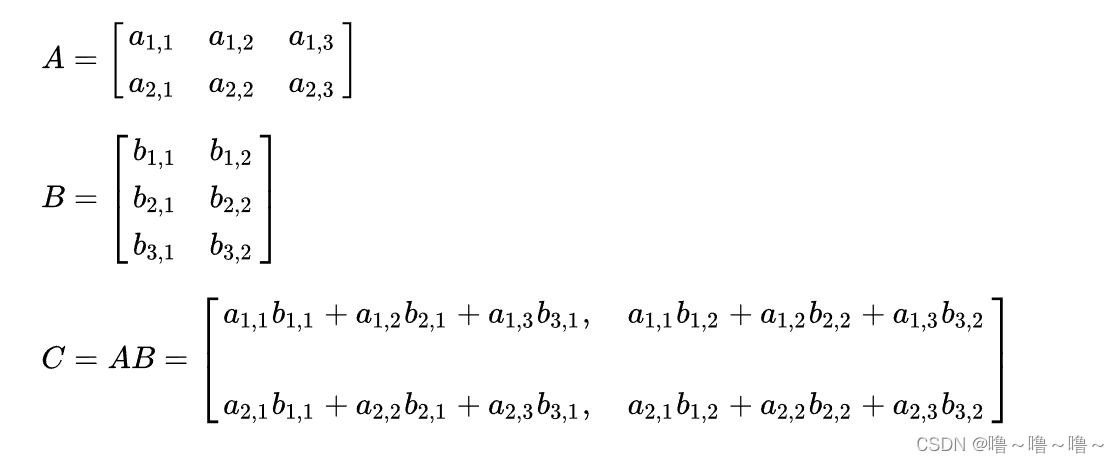
# 1. MATLAB 矩阵乘法基础**

MATLAB 矩阵乘法是 MATLAB 中一项基本且强大的运算，用于将两个矩阵相乘，生成一个新的矩阵。其语法为 `C = A * B`，其中 `A` 和 `B` 是要相乘的矩阵，`C` 是结果矩阵。

矩阵乘法遵循以下规则：

- 结果矩阵 `C` 的行数等于矩阵 `A` 的行数，列数等于矩阵 `B` 的列数。
- `C` 的第 `i` 行第 `j` 列的元素是矩阵 `A` 的第 `i` 行与矩阵 `B` 的第 `j` 列的元素的内积。

# 2. MATLAB 矩阵乘法在机器人技术中的理论应用

**2.1 机器人运动学建模**

机器人运动学建模是描述机器人运动的数学模型，它可以帮助我们了解机器人的运动规律，并为机器人控制和路径规划提供基础。MATLAB 矩阵乘法在机器人运动学建模中扮演着至关重要的角色。

**2.1.1 刚体变换矩阵**

刚体变换矩阵是一个 4x4 的矩阵，它可以描述刚体在三维空间中的平移和旋转。MATLAB 中可以使用 `transl` 和 `trotz` 函数来创建刚体变换矩阵。

% 创建一个沿 x 轴平移 1 米的刚体变换矩阵
T_x = transl(1, 0, 0);

% 创建一个绕 z 轴旋转 90 度的刚体变换矩阵
T_z = trotz(pi/2);

**2.1.2 齐次变换矩阵**

齐次变换矩阵是一个 4x4 的矩阵，它将刚体变换矩阵扩展为齐次坐标系，其中第四行是一个单位向量 `[0, 0, 0, 1]`。齐次变换矩阵可以表示刚体在三维空间中的平移、旋转和缩放。MATLAB 中可以使用 `homtrans` 函数来创建齐次变换矩阵。

% 创建一个沿 x 轴平移 1 米，绕 z 轴旋转 90 度的齐次变换矩阵
T_h = homtrans(T_x, T_z);

**2.2 机器人动力学建模**

机器人动力学建模是描述机器人运动时所受力的数学模型，它可以帮助我们了解机器人的运动特性，并为机器人控制提供基础。MATLAB 矩阵乘法在机器人动力学建模中也发挥着重要作用。

**2.2.1 牛顿-欧拉方程**

牛顿-欧拉方程是一组微分方程，它描述了机器人各关节的力矩和加速度之间的关系。MATLAB 中可以使用 `sym` 和 `solve` 函数来求解牛顿-欧拉方程。

% 创建机器人动力学模型的符号变量
syms q1 q2 q3 dq1 dq2 dq3 ddq1 ddq2 ddq3

% 定义机器人动力学模型的方程
eq1 = I1*ddq1 + I2*ddq2*cos(q2) + I3*ddq3*cos(q2+q3) + ...
       m1*g*L1*sin(q1) + m2*g*L2*sin(q1+q2) + m3*g*L3*sin(q1+q2+q3);
eq2 = I2*ddq2 + I3*ddq3*cos(q3) - m2*g*L2*sin(q1+q2) - m3*g*L3*sin(q1+q2+q3);
eq3 = I3*ddq3 - m3*g*L3*sin(q1+q2+q3);

% 求解牛顿-欧拉方程
sol = solve([eq1, eq2, eq3], [ddq1, ddq2, ddq3]);

**2.2.2 拉格朗日方程**

拉格朗日方程是一组微分方程，它描述了机器人各关节的广义力矩和广义速度之间的关系。MATLAB 中可以使用 `lagrangian` 和 `solve` 函数来求解拉格朗日方程。

% 创建机器人动力学模型的拉格朗日函数
L = 1/2*I1*dq1^2 + 1/2*I2*dq2^2 + 1/2*I3*dq3^2 + ...
     1/2*m1*L1^2*dq1^2 + 1/2*m2*L2^2*(dq1^2 + dq2^2) + ...
     1/2*m3*L3^2*(dq1^2 + dq2^2 + dq3^2) - ...
     m1*g*L1*cos(q1) - m2*g*L2*cos(q1+q2) - m3*g*L3*cos(q1+q2+q3);

% 求解拉格朗日方程
sol = lagrangian(L, [q1, q2, q3], [dq1, dq2, dq3]);

# 3. MATLAB 矩阵乘法在机器人技术中的实践应用

### 3.1 机器人正逆运动学求解

#### 3.1.1 正运动学求解

正运动学求解是指根据机器人的关节角度，计算末端执行器的位姿（位置和姿态）。MATLAB 中可以使用矩阵乘法来高效地求解正运动学。

% DH 参数表
dh_params = [theta, d, a, alpha; ...];

% 关节角度
joint_angles = [q1, q2, q3, ...];

% 计算齐次变换矩阵
T = eye(4);
for i = 1:num_joints
    T = T * DH_matrix(dh_params(i, :), joint_angles(i));
end

% 末端执行器位姿
end_effector_pose = T(1:3, 4);

**代码逻辑分析：**

* 使用 `DH_matrix` 函数根据 DH 参数和关节角度计算每个关节的齐次变换矩阵。
* 使用矩阵乘法将所有关节的齐次变换矩阵相乘，得到从基座到末端执行器的齐次变换矩阵。
* 从齐次变换矩阵中提取末端执行器的位姿（位置和姿态）。