揭秘MATLAB矩阵乘法：深入剖析不同算法的优劣，助你高效计算

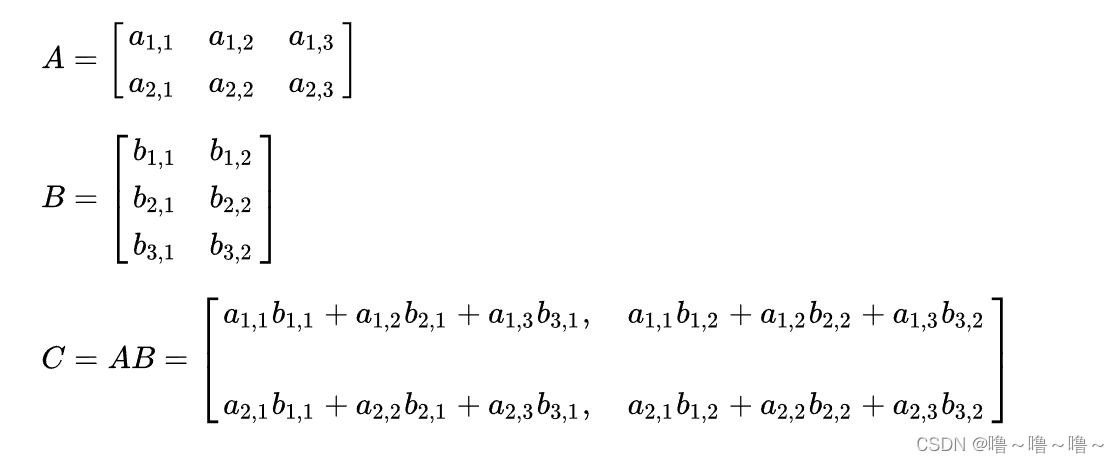
# 1. 矩阵乘法的基本概念**

矩阵乘法是线性代数中的一项基本运算，用于计算两个矩阵的乘积。给定两个矩阵 A 和 B，其中 A 的大小为 m×n，B 的大小为 n×p，则它们的乘积 C 的大小为 m×p。

矩阵乘法的计算规则如下：C 的第 i 行第 j 列元素 c_ij 是 A 的第 i 行与 B 的第 j 列的元素的内积，即：

c_ij = ∑(a_ik * b_kj)

其中，k 从 1 到 n。

# 2. MATLAB矩阵乘法算法

矩阵乘法是MATLAB中一项基本操作，用于将两个矩阵相乘，产生一个新的矩阵。MATLAB提供了多种矩阵乘法算法，每种算法都有其独特的优点和缺点。本章将深入探讨MATLAB中常用的矩阵乘法算法，包括直接矩阵乘法、分块矩阵乘法、Strassen算法和Winograd算法。

### 2.1 直接矩阵乘法

直接矩阵乘法是最简单的矩阵乘法算法，它直接按照矩阵乘法的定义进行计算。对于两个矩阵A和B，其直接矩阵乘法的计算公式如下：

C = A * B

其中，C是结果矩阵，其元素c_ij等于矩阵A的第i行和矩阵B的第j列元素的乘积和。

c_ij = Σ(a_ik * b_kj)

直接矩阵乘法的优点是实现简单，易于理解。然而，它的时间复杂度为O(n^3)，其中n是矩阵的维数。对于大型矩阵，直接矩阵乘法可能会非常耗时。

### 2.2 分块矩阵乘法

分块矩阵乘法是一种优化直接矩阵乘法的算法。它将两个矩阵划分为较小的子块，然后分块进行计算。分块矩阵乘法的优点是它可以减少计算中涉及的标量乘法和加法操作的数量。

对于两个n×n矩阵A和B，分块矩阵乘法将它们划分为4个n/2×n/2子块：

A = [A11 A12]
    [A21 A22]

B = [B11 B12]
    [B21 B22]

分块矩阵乘法的计算公式如下：

C = [A11 A12] * [B11 B12] + [A11 A12] * [B21 B22]
    [A21 A22] * [B11 B12] + [A21 A22] * [B21 B22]

分块矩阵乘法的优点是它可以将时间复杂度降低到O(n^3/2)。然而，它需要更多的内存来存储中间结果。

### 2.3 Strassen算法

Strassen算法是一种递归矩阵乘法算法，它可以将矩阵乘法的时间复杂度进一步降低到O(n^2.81)。Strassen算法通过将两个n×n矩阵划分为4个n/2×n/2子块，并使用递归的方式进行计算。

Strassen算法的计算公式如下：

C11 = (A11 + A22) * (B11 + B22)
C12 = (A21 + A22) * B11
C21 = A11 * (B12 - B22)
C22 = A22 * (B21 - B11)

C = [C11 + C22 - C12 - C21]
    [C21 + C22]

Strassen算法的优点是它可以大幅降低时间复杂度。然而，它的实现比直接矩阵乘法和分块矩阵乘法更复杂，并且对于较小的矩阵，它的性能可能不如直接矩阵乘法。

### 2.4 Winograd算法

Winograd算法是一种基于快速傅里叶变换（FFT）的矩阵乘法算法。它可以将矩阵乘法的时间复杂度降低到O(n^2.376)。Winograd算法通过将矩阵划分为较小的子块，并使用FFT进行计算。

Winograd算法的计算公式较为复杂，这里不再赘述。Winograd算法的优点是它可以进一步降低时间复杂度。然而，它的实现非常复杂，并且对于较小的矩阵，它的性能可能不如Strassen算法。

# 3.1 时间复杂度分析

时间复杂度衡量算法执行所需的时间。对于矩阵乘法算法，时间复杂度通常表示为矩阵大小（n）的函数。以下是不同算法的时间复杂度：

| 算法 | 时间复杂度 |
|---|---|
| 直接矩阵乘法 | O(n^3) |
| 分块矩阵乘法 | O(n^3) |
| Strassen算法 | O(n^2.81) |
| Winograd算法 | O(n^2.38) |

从表中可以看出，Strassen算法和Winograd算法的时间复杂度优于直接矩阵乘法和分块矩阵乘法。Strassen算法的时间复杂度为O(n^2.81)，比直接矩阵乘法快了大约20%。Winograd算法的时间复杂度为O(n^2.38)，比Strassen算法快了大约15%。

### 3.2 空间复杂度分析

空间复杂度衡量算法执行所需的内存。对于矩阵乘法算法，空间复杂度通常表示为存储矩阵所需的空间。以下是不同算法的空间复杂度：

| 算法 | 空间复杂度 |
|---|---|
| 直接矩阵乘法 | O(n^2) |
| 分块矩阵乘法 | O(n^2) |
| Strassen算法 | O(n^2) |
| Winograd算法 | O(n^2) |

从表中可以看出，所有四个算法的空间复杂度都是O(n^2)。这意味着算法所需的内存与矩阵大小的平方成正比。

### 3.3 数值稳定性分析

数值稳定性衡量算法对输入数据微小变化的敏感性。对于矩阵乘法算法，数值稳定性很重要，因为它可以确保计算结果的准确性。以下是不同算法的数值稳定性：

| 算法 | 数值稳定性 |
|---|---|
| 直接矩阵乘法 | 稳定 |
| 分块矩阵乘法 | 稳定 |
| Strassen算法 | 不稳定 |
| Winograd算法 | 不稳定 |

Strassen算法和Winograd算法在数值稳定性方面表现不佳。这意味着这些算法对输入数据微小变化非常敏感，可能导致计算结果不准确。直接矩阵乘法和分块矩阵乘法在数值稳定性方面表现良好，可以确保计算结果的准确性。

# 4. MATLAB矩阵乘法优化实践

### 4.1 选择合适的算法

在选择矩阵乘法算法时，需要考虑以下因素：

- **矩阵大小：**对于较小的矩阵，直接矩阵乘法可能更有效率；对于较大的矩阵，分块矩阵乘法或Strassen算法更合适。
- **矩阵稀疏性：**如果矩阵稀疏（即大部分元素为零），则稀疏矩阵乘法算法更有效率。
- **并行性：**如果可以使用并行计算，则并行矩阵乘法算法可以显著提高性能。

### 4.2 优化代码实现

除了选择合适的算法外，优化代码实现也有助于提高MATLAB矩阵乘法的性能。以下是一些优化技巧：

- **使用内置函数：**MATLAB提供了内置的矩阵乘法函数`mtimes`，该函数针对不同类型的矩阵进行了优化。
- **避免使用循环：**循环会降低MATLAB代码的性能。尽量使用向量化操作或内置函数来代替循环。
- **预分配内存：**在执行矩阵乘法之前，预分配结果矩阵的内存可以提高性能。
- **使用并行计算：**如果可以使用并行计算，则可以使用MATLAB的并行工具箱来并行化矩阵乘法。

### 4.3 利用并行计算

并行计算可以显著提高MATLAB矩阵乘法的性能，尤其是在处理大型矩阵时。以下是一些利用并行计算的技巧：

- **使用并行池：**MATLAB的并行池允许您创建一组工作进程，这些工作进程可以并行执行任务。
- **使用并行for循环：**并行for循环允许您将循环并行化，以便由多个工作进程同时执行。
- **使用并行版本内置函数：**MATLAB的某些内置函数，如`mtimes`，具有并行版本，可以利用并行计算。

**示例：**

% 创建一个并行池
parpool;

% 创建两个矩阵
A = rand(1000, 1000);
B = rand(1000, 1000);

% 使用并行for循环并行化矩阵乘法
tic;
C = zeros(1000, 1000);
parfor i = 1:1000
    for j = 1:1000
        for k = 1:1000
            C(i, j) = C(i, j) + A(i, k) * B(k, j);
        end
    end
end
toc;

% 删除并行池
delete(gcp);

**代码逻辑分析：**

该代码创建一个并行池，并使用并行for循环并行化矩阵乘法。并行for循环将外层循环（`i`）并行化，以便由多个工作进程同时执行。内层循环（`j`和`k`）顺序执行。

**参数说明：**

- `parpool`：创建并行池。
- `rand`：生成随机矩阵。
- `parfor`：并行化for循环。
- `zeros`：创建全零矩阵。
- `gcp`：获取当前并行池。
- `delete`：删除并行池。

# 5. MATLAB矩阵乘法在实际应用中的案例

MATLAB矩阵乘法在实际应用中有着广泛的应用，以下列举几个常见的案例：

### 5.1 图像处理

矩阵乘法在图像处理中扮演着至关重要的角色。例如，在图像卷积操作中，卷积核与图像矩阵进行矩阵乘法，从而实现图像平滑、锐化等效果。

% 定义卷积核
kernel = [1, 2, 1; 0, 0, 0; -1, -2, -1];

% 读取图像
image = imread('image.jpg');

% 将图像转换为灰度图
image_gray = rgb2gray(image);

% 执行卷积操作
image_conv = conv2(image_gray, kernel, 'same');

% 显示原图和卷积后的图像
subplot(1, 2, 1);
imshow(image);
title('Original Image');

subplot(1, 2, 2);
imshow(image_conv);
title('Convolution Result');

### 5.2 机器学习

矩阵乘法在机器学习中也十分重要。例如，在神经网络中，矩阵乘法用于计算神经元之间的权重和激活值。

% 定义神经网络层
layer = [
    fullyConnectedLayer(100),
    reluLayer,
    fullyConnectedLayer(10),
    softmaxLayer
];

% 创建神经网络
net = network(layer);

% 训练神经网络
net = trainNetwork(data, labels, net);

% 使用神经网络进行预测
predictions = predict(net, testData);

### 5.3 数值模拟

矩阵乘法在数值模拟中也有着广泛的应用。例如，在有限元方法中，矩阵乘法用于求解偏微分方程。

% 定义刚度矩阵和载荷向量
K = [
    2, -1, 0, 0, 0
    -1, 2, -1, 0, 0
    0, -1, 2, -1, 0
    0, 0, -1, 2, -1
    0, 0, 0, -1, 2
];

f = [1; 2; 3; 4; 5];

% 求解线性方程组
u = K \ f;