【C#中并行计算与IEEE 754】：浮点数转换的高级应用与性能优化


# 摘要
本文旨在探讨C#中的并行计算基础及其与IEEE 754标准的结合。首先介绍了并行计算的基本概念和实践技巧，包括并行框架的选择和线程同步通信。随后深入分析了IEEE 754标准在浮点数表示和精确控制中的应用，以及并行环境下浮点数性能优化的方法。文章还探讨了性能优化策略和并行计算在解决科学问题中的实际案例应用。通过对并行计算性能评估方法的介绍和案例分析，本文总结了并行计算技术的发展趋势和IEEE 754标准的未来应用前景。

# 关键字
并行计算；IEEE 754标准；浮点数表示；性能优化；线程同步；数值模拟

参考资源链接：[C# IEEE754浮点数转换详解及MODBUS应用实例](https://wenku.csdn.net/doc/ftp7s0tq61?spm=1055.2635.3001.10343)
# 1. C#中的并行计算基础

在当今的多核处理器时代，利用并行计算来提升软件性能已经变得至关重要。C#作为一门现代化的编程语言，从其设计之初就内置了支持并行处理的特性，这使得开发人员能够更有效地利用多核处理器资源。

## 1.1 并行计算的概念

并行计算是指同时使用多个计算资源解决计算问题的过程。这种计算方式能够显著加快数据处理速度，缩短程序运行时间。在C#中，开发者可以通过多种方式实现并行计算，包括使用线程、任务以及并行库等。

## 1.2 C#中的并行计算技术

C#中的并行计算技术主要包括以下几种：

- Task Parallel Library (TPL): TPL是.NET Framework的一部分，它提供了高级的API来编写异步和并行代码。
- PLINQ: 并行LINQ (PLINQ) 是LINQ的并行版本，能够在执行查询时自动并行化数据处理。
- Parallel类: 提供了一组方法，用于对代码块和集合进行并行执行。

接下来的章节将详细探讨IEEE 754标准与浮点数表示，并深入解析如何在C#中实现有效的并行计算。

# 2. IEEE 754标准与浮点数表示

### 2.1 IEEE 754标准简介

#### 2.1.1 标准的历史和发展

IEEE 754标准是计算机系统中表示浮点数的国际标准，自1985年首次发布以来，它已经成为硬件和软件在处理浮点运算时所普遍遵循的标准。IEEE 754标准的出现，为不同系统之间的浮点计算提供了一致性和兼容性，使得在不同的计算机系统上进行的科学计算能够得到相同或可预测的结果。

标准的制定历经数年，由多个版本不断完善，当前广泛使用的是1985年和2008年修订的版本。标准的发布极大地促进了数值计算领域的发展，尤其是对于需要高精度和复杂运算的科学计算、图形处理和数据分析等领域。

#### 2.1.2 浮点数的编码方式

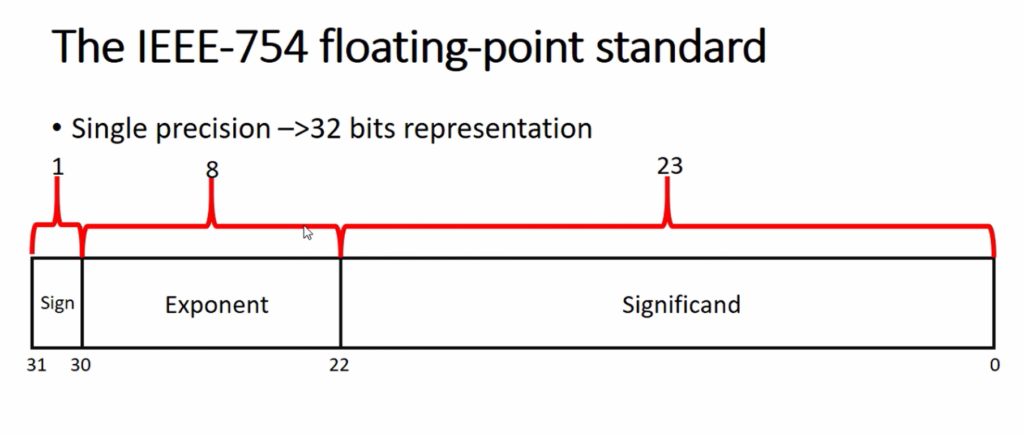
IEEE 754标准采用一种独特的编码方式来表示浮点数，主要包括三个部分：符号位、指数位和尾数位。这种结构不仅能够表示非常大或非常小的数值，还可以通过调整指数来控制数值的精度。具体来说：

- 符号位（S）：用来表示数值的正负，通常0代表正数，1代表负数。
- 指数位（E）：用来表示数值的大小，用于确定尾数的缩放大小。
- 尾数位（M）：也称作有效数字位，表示数值的精度，即小数点后的位数。

这种编码方式不仅能够精确地表示正负无穷大、正负零以及NaN（Not a Number）等特殊数值，还能通过舍入、规格化等操作确保计算的准确性。

### 2.2 C#中浮点数的运算规则

#### 2.2.1 浮点数的基本运算

在C#中，浮点数通常被表示为`float`和`double`类型，分别对应单精度和双精度浮点数。C#遵循IEEE 754标准进行浮点数的运算，使用了内建的硬件指令来执行这些运算。

基本的浮点运算包括加法、减法、乘法和除法。由于浮点数运算涉及到复杂的硬件执行逻辑和精度控制，因此开发者需要了解和掌握C#中浮点数运算的规则以编写出稳定且高效的代码。

float a = 1.234f;
float b = 5.678f;
float sum = a + b; // 加法
float difference = a - b; // 减法
float product = a * b; // 乘法
float quotient = a / b; // 除法

以上代码演示了C#中浮点数的四种基本运算。由于浮点数在计算机中的存储方式，这些运算可能会引入舍入误差。

#### 2.2.2 精度问题和舍入模式

浮点数运算的精度问题是开发者需要特别关注的，尤其是在涉及金融、科学计算等需要高精度计算的场景中。由于IEEE 754标准的浮点数表示是有限的，当进行复杂的数学运算时，可能会导致精度下降。

为了处理这些精度问题，IEEE 754标准定义了多种舍入模式，例如：最接近舍入、向零舍入、向下舍入和向上舍入。C#允许开发者设置当前线程的舍入模式，通过`System.Math`类可以访问和设置这些模式。

System.Math.Roound(a + b, MidpointRounding.AwayFromZero);

上述代码展示了如何使用`System.Math`类设置舍入模式，其中`MidpointRounding.AwayFromZero`表示当结果位于两个可表示的数的中间时，向远离零的方向舍入。

### 2.3 并行计算中的浮点数性能挑战

#### 2.3.1 并行计算对浮点性能的影响

随着多核处理器的普及，使用并行计算来提升性能已成为常见的做法。在并行计算环境中，多个线程或进程同时进行浮点数运算，这种并发执行对浮点性能提出了更高的要求。

并行计算环境中的浮点数性能会受到多种因素的影响，比如内存访问模式、线程同步机制以及处理器的缓存结构等。这些问题可能会导致浮点运算在并行环境下变得更加复杂。

Parallel.For(0, 1000, i => {
    float result = Process(i);
    // 累加结果
});

上面的代码示例展示了如何使用`Parallel.For`方法在C#中进行并行循环，进行浮点运算。

#### 2.3.2 如何评估和优化浮点性能

评估并行计算中浮点数的性能是确保应用程序高效运行的关键步骤。性能评估通常涉及到基准测试和性能分析工具的使用。基准测试可以帮助开发者理解代码的性能瓶颈，而性能分析工具则能提供更深入的性能数据。

优化并行计算中的浮点性能需要综合考虑算法的选择、数据的组织方式和计算任务的分配。优化策略可能包括：

- 使用锁或无锁的并发集合来减少线程间同步的开销。
- 实现负载平衡，确保每个线程或核心的工作量大致相同。
- 优化内存使用模式，减少缓存未命中和内存竞争的情况。

通过这些方法，开发者可以提升并行计算中的浮点性能，确保应用程序能够充分利用多核处理器的计算能力。

在本章节中，我们详细探讨了IEEE 754标准的历史、编码方式，以及在C#语言中如何理解和使用浮点数。此外，我们深入分析了并行计算环境下的浮点性能挑战，并提供了相应的评估和优化方法。这些知识为接下来的章节打下了坚实的基础，下一章我们将讨论C#在并行计算中的实践技巧。

# 3. C#中并行计算的实践技巧

## 3.1 并行框架与API选择

在现代编程中，尤其是在构建高性能的并行计算系统时，选择正确的并行框架和API至关重要。C#提供了多种并行编程模型，其中最著名的是Task Parallel Library (TPL)、并行LINQ（PLINQ）和并行集合操作。本节将详细介绍这些模型，并探讨其优缺点以及适用场景。

### 3.1.1 Task Parallel Library (TPL)基础

TPL 是.NET Framework 4中引入的一种模式和API，它简化了并行编程的复杂性，同时提供了比线程更高级别的抽象。TPL的核心概念是 `Task` 对象，它表示一个可能并行执行的工作单元。

**代码块示例:**

using System;
using System.Threading.Tasks;

class Program
{
    static void Main()
    {
        var task1 = Task.Factory.StartNew(() => Console.WriteLine("Task 1"));
        var task2 = Task.Factory.Star