数字信号处理习题集：理论与应用相结合的学习方式，开启高效学习之旅


参考资源链接：[《数字信号处理》第四版Sanjit-K.Mitra习题解答](https://wenku.csdn.net/doc/2i98nsvpy9?spm=1055.2635.3001.10343)
# 1. 数字信号处理基础概念

## 1.1 信号处理简史
数字信号处理（Digital Signal Processing，简称DSP）在信息技术中占据着核心地位，其发展历程始于20世纪60年代。在模拟电子时代，信号通过模拟电路进行处理，但随着微电子和计算技术的发展，数字处理方式以其优异的稳定性和灵活性逐渐取代了模拟方式。数字信号处理的基础是对连续信号进行离散化，通过离散时间信号的分析和处理，实现信号的各种变换与应用。

## 1.2 信号与系统的基本概念
在数字信号处理中，信号可以视为信息的载体，而系统则为处理信号的装置或算法。信号根据其连续性或离散性可分为连续时间信号和离散时间信号。系统则根据其处理信号方式的不同，可以分为线性时不变系统（LTI系统）和非线性时变系统等。了解这些基础概念是深入研究数字信号处理的起点。

## 1.3 数字信号处理的应用范畴
数字信号处理广泛应用于通信、音频、视频、图像处理、医学成像、雷达、声纳等众多领域。例如，数字滤波器用于从信号中去除噪声，而傅里叶变换则被广泛用于频谱分析中。数字信号处理不仅提高了信号处理的精确度和效率，还大大扩展了信号处理的应用范围和能力。随着技术的不断进步，数字信号处理的重要性将继续增长。

# 2. 数字信号处理的核心理论

### 2.1 离散时间信号与系统

#### 2.1.1 信号的基本分类和特性

离散时间信号是数字信号处理的基础，其定义为一系列在离散时间点上定义的值。信号的分类主要包含确定性信号和随机信号。

- **确定性信号**：这类信号的值可以预先确定，如正弦波、方波和锯齿波等。它们通常用于理论分析和信号模型的建立。

- **随机信号**：随机信号的值不能预先确定，具有不可预测性，通常用统计学的方法来分析，如噪声信号。

信号的特性通常可以从其时域和频域两个角度来分析。时域特性描述了信号随时间变化的规律，而频域特性则揭示了信号中不同频率成分的组成。

#### 2.1.2 系统的时域和频域分析

系统是处理输入信号并产生输出信号的物理设备或数学模型。在数字信号处理中，系统分析通常分为时域分析和频域分析两种方法。

- **时域分析**：主要通过系统对信号的响应来观察系统特性，常用的响应包括冲激响应和阶跃响应。

- **频域分析**：将信号分解为不同频率的正弦波，并分析这些正弦波如何通过系统。傅里叶变换是频域分析中不可或缺的工具。

### 2.2 傅里叶分析与Z变换

#### 2.2.1 傅里叶变换的基本概念和应用

傅里叶变换是一种将时间域信号转换为频域表示的方法，它揭示了信号的频率成分。在数字信号处理中，通常使用离散傅里叶变换（DFT）及其快速算法——快速傅里叶变换（FFT）。

傅里叶变换的应用极为广泛，包括信号滤波、频谱分析、信号压缩和解压缩等。例如，在音频信号处理中，通过傅里叶变换可以识别出混合信号中的各个音源。

% MATLAB中傅里叶变换的应用示例
x = [1 2 3 4]; % 原始信号
X = fft(x); % 执行FFT
f = (0:length(X)-1)*Fs/length(X); % 频率向量
plot(f,abs(X)); % 绘制信号的幅度谱
title('信号的幅度频谱');
xlabel('频率(Hz)');
ylabel('|X(f)|');

在这个MATLAB代码块中，我们首先定义了一个简单的时域信号，接着使用`fft`函数来计算其DFT，然后得到对应的频率向量，并最终绘制了信号的幅度频谱。

#### 2.2.2 Z变换的原理和计算方法

Z变换是离散时间信号的另一种重要变换，它将时域信号转换为复频域表示。Z变换是分析线性时不变离散系统的一种有效方法，对于系统稳定性的判断以及系统函数的求解具有重要作用。

Z变换的一个基本性质是线性，这意味着两个信号和的Z变换等于各自Z变换的和。

% MATLAB中Z变换的应用示例
syms n z;
x = sym([1 2 3 4]); % 符号表示的离散时间信号
X = ztrans(x,n,z); % 计算Z变换
pretty(X) % 美化输出结果

在这个MATLAB代码块中，我们使用符号计算工具箱中的`ztrans`函数来计算离散时间信号`x`的Z变换`X`，`pretty`函数则用于以更为可读的格式输出Z变换的结果。

### 2.3 数字滤波器设计

#### 2.3.1 滤波器的分类与特性

滤波器是数字信号处理中用于修改、限制或者筛选信号频率成分的系统。常见的滤波器类型包括低通、高通、带通和带阻滤波器。

每种滤波器都有其特定的频率特性，例如：
- **低通滤波器**：允许低频信号通过，抑制高频信号。
- **高通滤波器**：允许高频信号通过，抑制低频信号。
- **带通滤波器**：允许特定范围内的频率信号通过，抑制其它频率。
- **带阻滤波器**：抑制特定范围内的频率信号，允许其它频率通过。

滤波器的设计需要满足特定的技术指标，如截止频率、过渡带宽度、通带和阻带衰减等。

#### 2.3.2 滤波器设计的数学方法

滤波器设计的数学方法通常包括窗函数法和频率采样法。其中，窗函数法是设计FIR滤波器的常用方法。

使用窗函数法设计滤波器，通常步骤如下：

1. 确定滤波器的性能指标，如通带和阻带频率、过渡带宽度和通带波纹等。
2. 根据性能指标计算理想滤波器的冲击响应。
3. 选择一个合适的窗函数来减小旁瓣，改善滤波器的性能。
4. 应用窗函数到理想滤波器冲击响应上，得到实际滤波器系数。

使用MATLAB可以简化滤波器设计的步骤，例如：

% MATLAB中FIR滤波器设计示例
N = 50; % 滤波器阶数
Wn = 0.3; % 归一化截止频率
windowType = 'hamming'; % 窗函数类型
b = fir1(N, Wn, windowType); % 计算滤波器系数
freqz(b,1,1024); % 绘制滤波器的频率响应

通过执行这段MATLAB代码，我们可以设计一个低通FIR滤波器，并绘制出其频率响应特性曲线。

在下一章节中，我们将继续探讨数字信号处理的实践技巧，包括信号的采样与重构，窗函数在信号处理中的应用以及信号的数字处理实现等主题。这些内容将帮助我们进一步深入理解数字信号处理的实际应用和技术细节。

# 3. 数字信号处理实践技巧

在前一章中，我们探讨了数字信号处理的核心理论基础。这一章将带领您从理论走向实践，深入理解数字信号处理中实用技巧的应用。通过实践，您可以更加直观地感受到理论知识与现实世界的联系。

## 3.1 信号的采样与重构

数字信号处理的一个核心步骤是对模拟信号进行采样，将其转换为数字形式。采样过程遵循奈奎斯特采样定理，而信号重构则是采样过程的逆过程，目的是尽可能无损地恢复原始的模拟信号。

### 3.1.1 采样定理的理解和应用

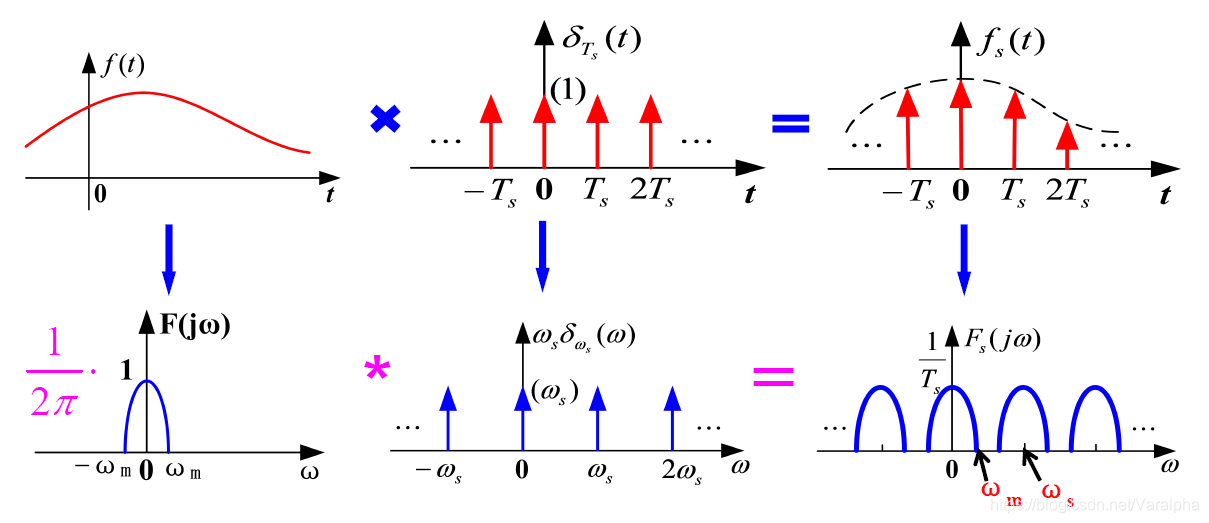
奈奎斯特采样定理，也被称为采样定理，是数字信号处理中最重要的定理之一。它规定，如果一个信号是带限的，并且带宽有限，则采样频率必须大于信号最高频率的两倍，采样后的信号才能无失真地被重构。

在实际应用中，当采样频率不够高时，会发生混叠现象，即高频信号的频率分量折叠到低频部分。因此，合理选择采样频率和抗混叠滤波器设计是保证信号能够正确采样的关键。

### 3.1.2 信号重构的算法和实践

采样后的数字信号通过数字到模拟转换器(DAC)进行重构。信号重构的常见算法包括零阶保持和sinc插值等。零阶保持方法简单，但会造成较多的锯齿状失真；sinc插值则能够提供更平滑的重构信号，但计算量较大。

在编程实践中，可以使用各种数字信号处理库来实现信号的采样与重构。例如，在Python中，可以使用SciPy库中的signal模块来实现这一过程。

### 示例代码

import numpy as np
from scipy.signal import resample
import matplotlib.pyplot as plt

# 创建一个模拟信号
t = np.linspace(0, 1, 200, endpoint=False)
data = np.sin(2*np.pi*5*t)

# 采样
fs = 100.0  # 采样频率
data_sampled = resample(data, int(fs))

# 重构信号，使用sinc插值
t_reconstruct = np.linspace(0, 1, 1000, endpoint=False)
data_reconstruct = np.zeros_like(t_reconstruct)
for i in range(len(data)):
    data_reconstruct += data_sampled[i] * np.sinc(fs*t_reconstruct - i)

# 绘制信号
plt.figure(figsize=(15, 5))
plt.subplot(1, 3, 1)
plt.plot(t, data, label='Original')
plt.legend()
plt.subplot(1, 3, 2)
plt.plot(np.arange(len(data_sampled))/fs, data_sampled, label='Sampled')
plt.legend()
plt.subplot(1, 3, 3)
plt.plot(t_reconstruct, data_reconstruct, label='Reconstructed')
plt.legend()
plt.show()

在这段代码中，我们首先创建了一个模拟信号，然后使用`resample`函数进行采样。之后，我们使用`sinc`函数来进行信号重构。

## 3.2 窗函数在信号处理中的应用

在进行频谱分析时，窗函数的选择至关重要，它能够影响到分析结果的准确度和分辨率。

### 3.2.1 窗函数的类型和选择

窗函数有很多种，如汉宁窗、汉明窗、布莱克曼窗等。每种窗函数都有其特定的用途和特性。例如，汉宁窗具有较低的旁瓣水平，但在主瓣宽度上牺牲了一些频率分辨率；汉明窗则在两者之间取得了折中。

选择合适的窗函数需要根据信号的特