SLAM导航中的定位与建图：算法与实现全解析

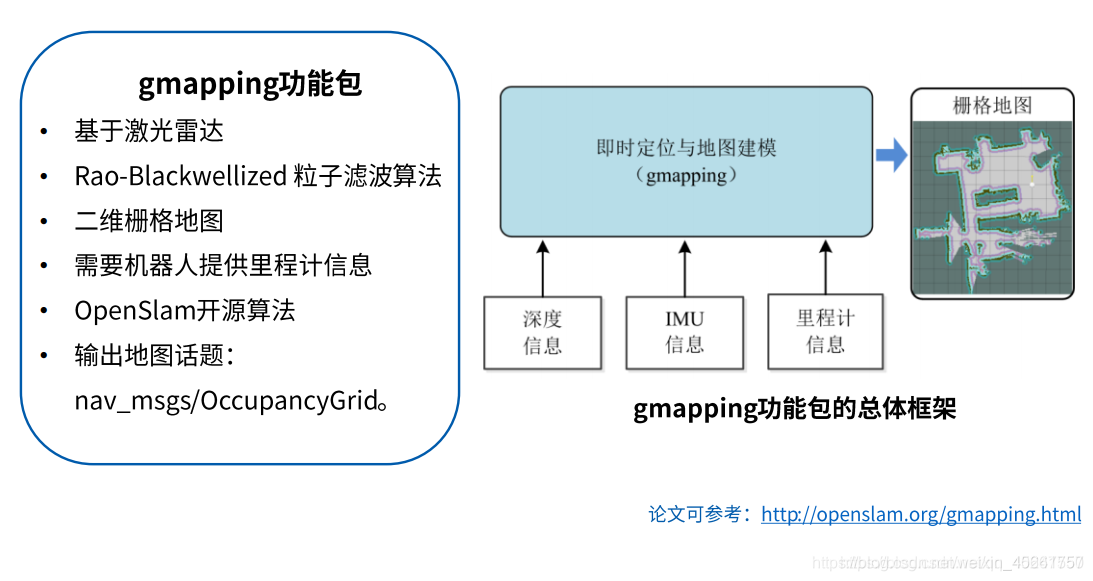
# 1. SLAM导航概述

SLAM（即时定位与地图构建）是一种机器人技术，它使机器人能够在未知环境中自主导航和构建地图。SLAM算法融合来自传感器的数据（如激光雷达、视觉传感器）来估计机器人的位置和周围环境的地图。

SLAM导航的主要挑战在于处理不确定性和传感器噪声。机器人必须能够处理传感器数据中的不确定性，并随着时间的推移更新其位置和地图估计。此外，SLAM算法必须高效且实时，以使机器人能够在动态环境中导航。

SLAM导航在各种应用中都有广泛应用，包括室内导航、自动驾驶和机器人探索。通过提供机器人对周围环境的实时理解，SLAM技术使它们能够安全有效地执行复杂的任务。

# 2. 定位算法

### 2.1 粒子滤波

#### 2.1.1 基本原理

粒子滤波是一种基于蒙特卡罗方法的定位算法，它通过维护一组粒子（即假设的机器人位姿）来估计机器人的真实位姿。每个粒子都携带一个权重，该权重反映了粒子与传感器观测值匹配的程度。

#### 2.1.2 蒙特卡罗方法

蒙特卡罗方法是一种通过随机采样来解决复杂问题的技术。在粒子滤波中，粒子集代表了机器人的位姿分布。通过对粒子集进行采样和加权，粒子滤波可以估计机器人位姿的后验概率分布。

### 2.2 卡尔曼滤波

#### 2.2.1 状态空间模型

卡尔曼滤波是一种基于状态空间模型的定位算法。状态空间模型由两个方程组成：状态转移方程和观测方程。状态转移方程描述了机器人位姿随时间的变化，而观测方程描述了传感器观测值与机器人位姿之间的关系。

#### 2.2.2 预测和更新步骤

卡尔曼滤波算法包含两个主要步骤：预测和更新。在预测步骤中，滤波器使用状态转移方程预测机器人的位姿。在更新步骤中，滤波器使用观测方程将预测的位姿与传感器观测值相结合，以更新机器人的位姿估计。

### 2.3 扩展卡尔曼滤波

#### 2.3.1 非线性系统建模

卡尔曼滤波假设状态转移方程和观测方程都是线性的。然而，在实际的SLAM系统中，这些方程通常是非线性的。扩展卡尔曼滤波（EKF）是一种扩展卡尔曼滤波，它通过使用一阶泰勒展开来线性化非线性方程。

#### 2.3.2 扩展卡尔曼滤波算法

EKF算法与卡尔曼滤波算法类似，但它在预测和更新步骤中使用了线性化的状态转移方程和观测方程。

# 预测步骤
x_pred = f(x_prev)
P_pred = F * P_prev * F.T + Q

# 更新步骤
K = P_pred * H.T * (H * P_pred * H.T + R).inv()
x_est = x_pred + K * (z - h(x_pred))
P_est = (I - K * H) * P_pred

其中：

* `x_prev` 为前一时间步的位姿估计
* `x_pred` 为预测的位姿
* `P_prev` 为前一时间步的协方差矩阵
* `P_pred` 为预测的协方差矩阵
* `f` 为状态转移函数
* `F` 为状态转移雅可比矩阵
* `Q` 为过程噪声协方差矩阵
* `z` 为传感器观测值
* `h` 为观测函数
* `H` 为观测雅可比矩阵
* `R` 为观测噪声协方差矩阵
* `I` 为单位矩阵

# 3. 建图算法

### 3.1 栅格地图

**3.1.1 地图表