MATLAB数据降维与特征选择：提取关键信息，提升模型性能，让数据分析更具针对性

# 1. MATLAB数据降维与特征选择概述**

数据降维是一种将高维数据映射到低维空间的技术，用于降低数据的复杂性并提取其关键特征。特征选择则从原始数据集中选择出最相关的特征，以提高模型的性能和可解释性。

MATLAB提供了一系列用于数据降维和特征选择的函数和工具箱。这些工具可以帮助数据科学家和机器学习工程师有效地处理高维数据，提高模型的准确性和效率。

# 2. 理论基础

### 2.1 数据降维技术

数据降维是一种将高维数据映射到低维空间的技术，其目的是在保留原始数据中重要信息的同时减少数据维度。常用的数据降维技术包括：

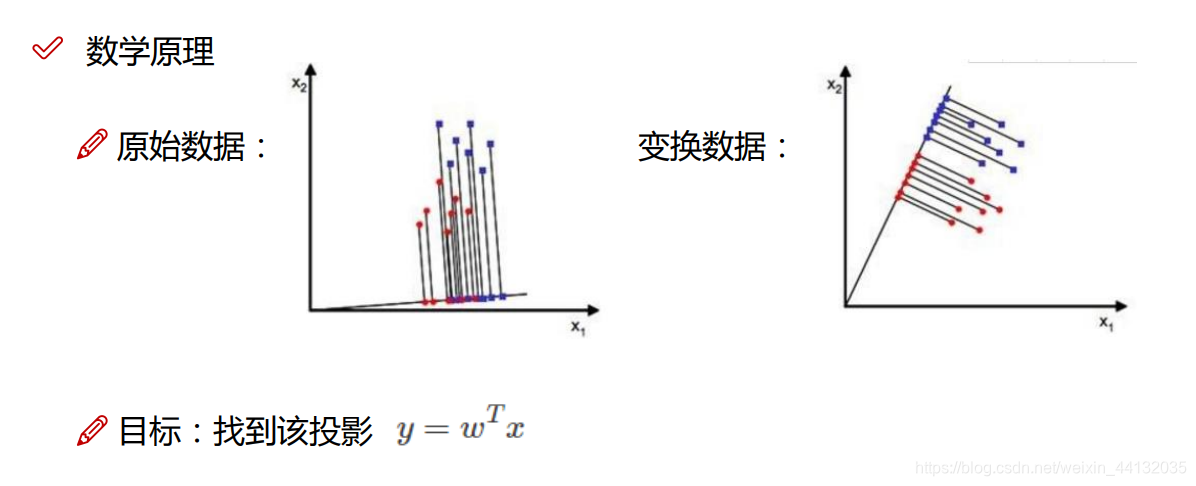
#### 2.1.1 主成分分析（PCA）

PCA是一种线性降维技术，它通过寻找原始数据中方差最大的方向来构造降维后的数据。PCA的原理是将原始数据投影到由这些方向组成的子空间上，从而获得低维表示。

**代码块：**

% 导入数据
data = csvread('data.csv');

% 计算协方差矩阵
covariance_matrix = cov(data);

% 计算特征值和特征向量
[eigenvectors, eigenvalues] = eig(covariance_matrix);

% 排序特征值
[sorted_eigenvalues, indices] = sort(eigenvalues, 'descend');

% 选择前k个特征向量
k = 2;
selected_eigenvectors = eigenvectors(:, indices(1:k));

% 将数据投影到降维后的空间
reduced_data = data * selected_eigenvectors;

**逻辑分析：**

* `cov(data)` 计算原始数据的协方差矩阵，其中协方差表示不同特征之间的相关性。
* `eig(covariance_matrix)` 计算协方差矩阵的特征值和特征向量，特征值表示方差的大小，特征向量表示方差的方向。
* `sort(eigenvalues, 'descend')` 对特征值进行降序排序，以确定方差最大的方向。
* `selected_eigenvectors` 选择前k个特征向量，k表示要降维到的维度。
* `data * selected_eigenvectors` 将原始数据投影到降维后的空间，从而获得低维表示。

#### 2.1.2 奇异值分解（SVD）

SVD是一种比PCA更通用的降维技术，它适用于线性或非线性数据。SVD将原始数据分解为三个矩阵的乘积：左奇异矩阵、奇异值矩阵和右奇异矩阵。奇异值表示原始数据中方差最大的方向。

**代码块：**

% 导入数据
data = csvread('data.csv');

% 奇异值分解
[U, S, V] = svd(data);

% 选择前k个奇异值
k = 2;
reduced_data = U(:, 1:k) * S(1:k, 1:k) * V(:, 1:k)';

**逻辑分析：**

* `svd(data)` 对原始数据进行奇异值分解，得到左奇异矩阵U、奇异值矩阵S和右奇异矩阵V。
* `U(:, 1:k) * S(1:k, 1:k) * V(:, 1:k)'` 选择前k个奇异值，并将其与奇异矩阵相乘，得到降维后的数据。

#### 2.1.3 线性判别分析（LDA）

LDA是一种监督降维技术，它考虑了类标签信息。LDA的目标是找到一个投影方向，使不同类别的样本在投影后的空间中尽可能分开。

**代码块：**

% 导入数据
data = csvread('data.csv');
labels = csvread('labels.csv');

% 构建LDA模型
lda_model = fitcdiscr(data, labels);

% 将数据投影到LDA空间
reduced_data = lda_model.transform(data);

**逻辑分析：**

* `fitcdiscr(data, labels)` 构建LDA模型，其中data是原始数据，labels是类标签。
* `lda_model.transform(data)` 将原始数据投影到LDA空间，得到降维后的数据。

### 2.2 特征选择方法

特征选择是一种从原始数据中选择最具信息性和相关性的特征的技术。常用的特征选择方法包括：

#### 2.2.1 过滤法

过滤法根据特征的固有属性（如方差、信息增益）对特征进行评分，然后选择得分最高的特征。

**代码块：**

% 导入数据
data = csvread('data.csv');

% 计算特征方差
variances = var(data);

% 选择方差最大的k个特征
k = 2;
selected_features = find(variances >= max(variances) - k * std(variances));

**逻辑分析：**

* `var(data)` 计算每个特征的方差。
* `find(variances >= max(variances) - k * std(variances))` 找到方差最大的k个特征。

#### 2.2.2 包裹法

包裹法将特征选择视为一个优化问题，它通过评估不同特征组合的分类或回归模型性能来选择特征。

**代码块：**

% 导入数据
data = csvread('data.csv');
labels = csvread('labels.csv');

% 构建包裹法模型
wrapper_model = SequentialFeatureSelector('Direction', 'forward');

% 训练模型
wrapper_model.train(data, labels);

% 获取选择的特征
selected_features = wrapper_model.SelectedFeatures;